Question

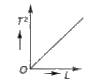
The graph between L and $T^2$ is

Options

A.
B.
C.
D.

Answer

A

Explanation

To determine the relationship between the length of a pendulum (L) and the square of its time period (T²), we can follow these steps:

1. Understand the Formula for Time Period of a Simple Pendulum:
The time period (T) of a simple pendulum is given by the formula:
\( T = 2\pi \sqrt{\frac{L}{g}} \)
where \(g\) is the acceleration due to gravity.

2. Square the Time Period Formula:
To find the relationship between \(L\) and \(T^2\), we square both sides of the equation:
\( T^2 = (2\pi)^2 \cdot \frac{L}{g} \)
This simplifies to:
\( T^2 = \frac{4\pi^2}{g} \cdot L \)

3. Identify the Relationship:
From the equation \(T^2 = \frac{4\pi^2}{g} \cdot L\), we can see that \(T^2\) is directly proportional to \(L\). This means that as the length \(L\) increases, \(T^2\) also increases.

4. Graphical Representation:
When plotting \(T^2\) on the y-axis and \(L\) on the x-axis, the graph will be a straight line. This is because of the direct proportionality established in the previous step.

5. Conclusion:
The graph between \(L\) and \(T^2\) will be a straight line, indicating a linear relationship.

Final Answer:
The graph between \(L\) and \(T^2\) is a straight line.

---