StateP1,V1,T1ARev−−→State BP2,V2,T2: If P1=P2 thenSolution in Telugu
ΔSuniverse=0
ΔSuniverse=1
ΔSuniverse>0
ΔSuniverse<0
The correct Answer is:A
For reversible isobaric process ΔSsystem=ncPlnT2T1,ΔSsurr=−ncPlnT2T1
∴ΔSuniverse=0
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - CHEMICAL THERMODYNAMICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II LECTURE SHEET (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)7videos
CHEMICAL THERMODYNAMICS
- BOOK - AAKASH SERIESCHAPTER - CHEMICAL THERMODYNAMICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II LECTURE SHEET (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)2videos
CHEMICAL THERMODYNAMICS
- BOOK - AAKASH SERIESCHAPTER - CHEMICAL THERMODYNAMICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - I (MAIN))13videos
CHEMICAL THERMODYNAMICS
- BOOK - AAKASH SERIESCHAPTER - CHEMICAL THERMODYANMICS EXERCISE - Questions For Descriptive Answers28videos
CHEMICAL THERMODYANMICS
- BOOK - AAKASH SERIESCHAPTER - ELECTRON MIGRATION EFFECTS EXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS10videos
ELECTRON MIGRATION EFFECTS
Similar Questions
Temperature of an ideal gas increases in:
05:14View SolutionA flask of 1L having NH3(g) at 2.0atm and 200K is connected with another flask of vol 800ml having HCl(g) at 8atm & 200K through tube of negligible volume. The two gases reacts to form NH4Cl(s) with evolution of 43 KJ/mol heat. If heat capacity of at constant volume is 20J/K/mol and neglecting heat capacity of flask and solid, volume of solid formed and its pressure (R = 0.08).
The final pressure in the flask is03:06View SolutionWhich among the following is not an exact differential?
04:03View SolutionHow does heat of neutralisation value change with the chemical nature of acid and base?
View SolutionHyperconjugation effect is also termed as 'no bond resonance'. Why?
View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
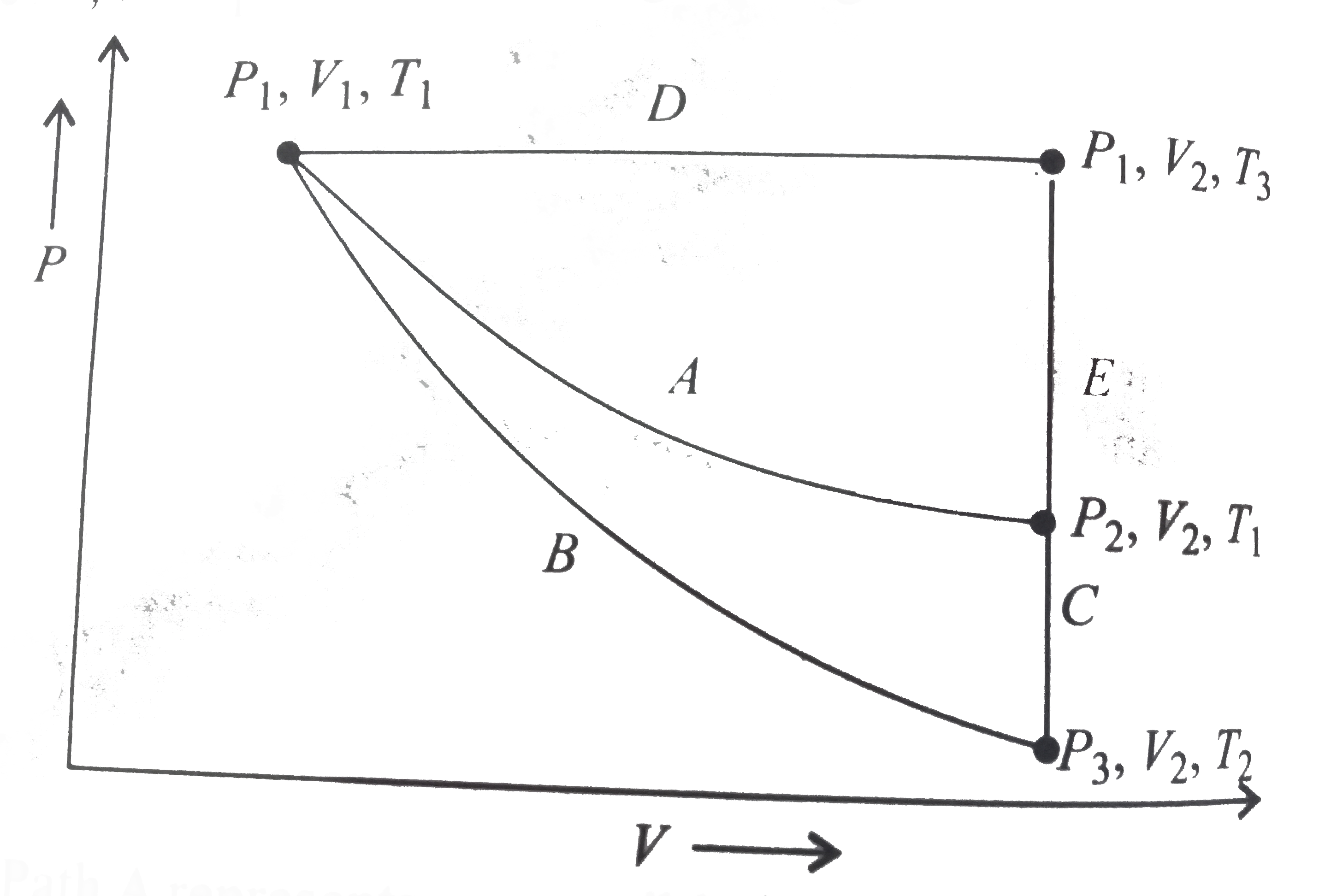
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (A)?11:56View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P_(1), V_(1), T_(1) to a final state P_(2), V_(2),T_(1) is shown in the given figure. Path A represents a reversible isothermal expansion form P_(1),V_(1) to P_(2),V_(2) , Path (B+C) represents a reversible adiabatic expansion (B) from P_(1),V_(1),T_(1)to P_(3),V_(2),T_(2) followed by reversible heating the gas at constant volume (C) from P_(3),V_(2),T_(2) to P_(2),V_(2),T_(1) . Path (D+E) represents a reversible expansion at constant pressure P_(1)(D) from P_(1),V_(1),T_(1) to P_(1),V_(2),T_(3) followed by a reversible cooling at constant volume V_(2)(E) from P_(1),V_(2),T_(3) to P_(2),V_(2),T_(1) . What is q_(rev) , for path (B +C) ?
03:18View SolutionFor an ideal gas, an illustratio of three different paths A(B+C) and (D+E) from an initial state P1,V1,T1 to a final state P2,V2,T1 is shown in the given figure.
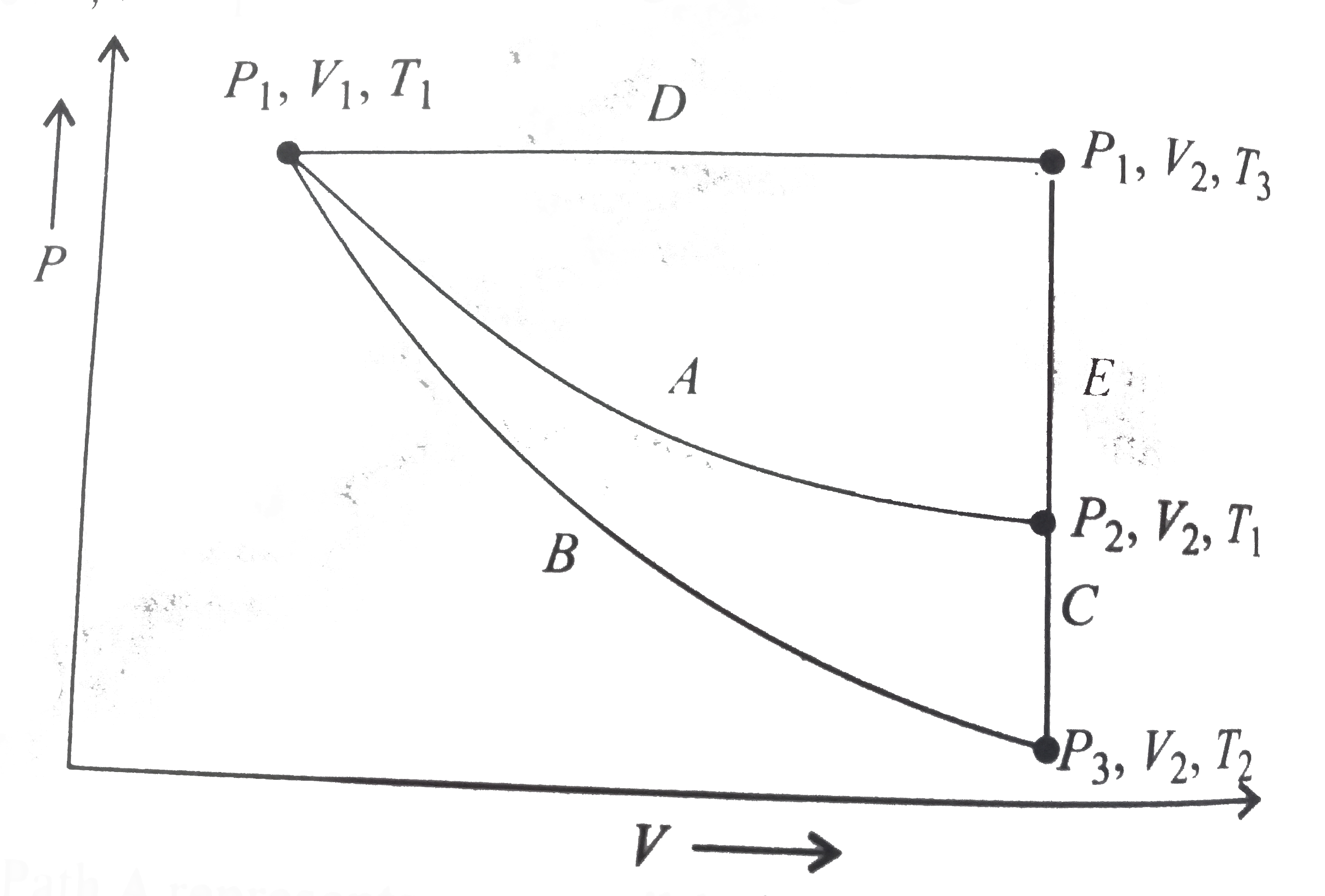
Path Arepresents a reversible isothermal expansion form P1,V1 to P2,V2, Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1→P3,V2,T2 followed by reversible heating the gas at constant volume (C)from P3,V2,T2 to P2,V2,T1. Path (D+E) represents a reversible expansion at constant pressure P1(D) from P1,V1,T1 to P1,V2,T3 followed by a reversible cooling at constant volume V2(E) from P1,V2,T3→P2,V2,T1.
What is qrev, for path (D+E)?05:56View SolutionAn ideal gasa undergoes through folowing cyclic procees. 1-2 : Reversible adialbatic comparession from P_(1)V_(1)T_(1)"to"P_(2)V_(2)T_(2) 2-3 : Reversible isochoric heating from P_(2)V_(2)T_(2)" to " P_(3)V_(3)T_(3) 3-4 Reversible adialbatic expansion from P_(3)V_(3)T_(3)" to " P_(4)V_(4)T_(4) 4-1 Reversible isochoric cooling from P_(4)V_(4)T_(4)" to " P_(1)V_(1)T_(1) Eefficiencyof the cycle is :
02:26View SolutionFor an ideal monoatomic gas, an illustration of three different paths A,(B+C) and (D+E) from an initial state P_(1),V_(1),T_(1) to a final state P_(2),V_(2),T_(1) is shown in the given figure . Path A represents a reversible isothermal from P_(1)V_(1)" to "P_(2),V_(2) , path (B+C) represent a reversible adiabatic expansion (B) from P_(1),V_(1),T_(1)" to " P_(3),V_(2),T_(2) followed by reversible heating of the gas at constant volume (C) from P_(3),V_(2),T_(2) " to " P_(2),V_(2),T_(1) . Path (D+E) represents a reversible expansion at constant pressure P_(1)(D) from P_(1),V_(1),T_(1) " to "P_(1),V_(2),T_(3) followed by a reversible cooling at constant volume V_(2)(E) form P_(1),V_(2),T_(3) " to "P_(2),V_(2),T_(1) What is q_("rev") for path (A)?
02:50View SolutionExamine the following plots and predict whether in (i) P_(1) lt P_(2) "and" T_(1) gt T_(2) , in (ii) T_(1) = T_(2)ltT_(3) , in (iii) V_(1) gt V_(2), "in" (iv) P_(1) gt P_(2) "or" P_(2) gt P_(1)
01:54View SolutionThe initial pressure, temperature & volume of 1 mol of a gas are P1,T1andV1 respectively. The state of the gas is changed by the following two ways. Will the internal energy change be the same in both cases?
(1) P1V1T2Reversible−−−−−→ProcessP2V2T2
(2) P1V1T1Irreversible−−−−−−→processP2V2T2.View SolutionEstablish gas equation, (P_(1)V_(1))/(T_(1))=(P_(2)V_(2))/(T_(2)) .
03:22View SolutionA system Xundergoes following changes
XP1V1T1→WP2V2T1→ZP3V2T2→XP1V1T1
The overall process may be called as04:01View SolutionA sample of gas changes from p1,V1 and p2. V2andT2 by one path and then back to p1,V1andT1. ΔU for the process is :
05:41View Solution

