A cylindrical piece of cork of density of base area A and height h floats in a liquid of density pl. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hpp1g
where p is the density of cork. (Ignore damping due to viscosity of the liquid).Solution in Gujrati
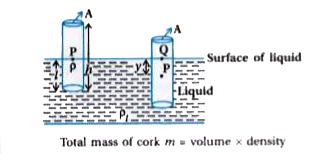
Total mass of cork m = volume × density
= Area × height × density
∴m=Ahp ……(1)
When the cork is depressed in liquid, the mass of displacement liquid,
m. = cross sectional area of cork × length of depressed part of cork × density of liquid × g
∴m.=Alpl
From the floating law of body.
Weight of cork in air = weight of cork in liquid
mg−m.g,Ahpg=Alplg
∴h=lplp ........(2)
Suppose the cork is depressed by PQ=y, then the restoring force acting on it,
F=−[ mass of cylindrical height of liquid ]×g×y
=−(Ayplg)y=−ky
Where force constant k=Aplg .......(3)
The time period of oscillation of cork, T=2π√mk
=2π√AhpAplg [∴ From equation (1) and (2) ]
∴T=2π√hpplg is proved
This formula is the time period of simple pendulum because,
T=2π√pllp×pplg (from equation (2))
therforeT=2π√lg.
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-B (ADDITIONAL EXERCISE)9videos
OSCILLATIONS
- BOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-B (NUMERICAL FROM DARPAN BASED ON TEXTBOOK)15videos
OSCILLATIONS
- BOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-B (NUMERICAL FROM TEXTUAL ILLUSTRATIONS)40videos
OSCILLATIONS
- BOOK - KUMAR PRAKASHANCHAPTER - OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE EXERCISE - CHAPTER - 8 (Match Type questions)5videos
OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE
- BOOK - KUMAR PRAKASHANCHAPTER - PHYSICAL WORLDEXERCISE - SECTION-E (QUESTIONS FROM MODULE)9videos
PHYSICAL WORLD
Similar Questions
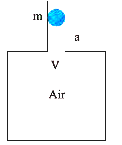
An air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
06:44View SolutionThe displacement of a simple harmonic oscillator is given by y=0.40sin(440t+0.61). For this, what are the value of amplitude.
02:16View SolutionOn an average, a human heart is found to beat 75 times in a minute. Calculate its frequency and period.
07:27View SolutionType of satellites are given in Column-I and their uses are given in Column-II. Match them properly :
Column-IColumn-II(1) Polar satellite(a) Tele communication(2) Geo-stationary satellite(b) Investigation(c) For information about atmosphere07:24View Solution.…. state of substance at very high temperature has generated hope of energy source for mankind.
09:47View SolutionA cylindrical piece of cork of base area A and height h floats in a liquid of density rho_(1) . The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period T=2pisqrt((hrho)/(rho_(1)g))
07:58View SolutionA cylidrical wooden piece of cork floats in a liquid of density σ. The cork is depressed slightly and released. Show that the cork will oscillate up and down simple harmonicaly with a period.
T=2π√ρhσg, where ρ is the density of the cork.03:57View Solutionआधार क्षेत्रफल A तथा ऊँचाई h के एक कॉर्क का बेलनकार दुकड़ा pt घनत्व के किसी द्रव में तैर रहा है | कॉर्क को थोड़ा निचे दबाकर स्वतंत्र छोड़ देते है, यह दर्शाइए कि कॉर्क ऊपर-निचे सरल आवर्त दोलन करता है जिसका आवर्तकाल
T=2π√hpp1g है |
यहाँ p कॉर्क का घनत्व है (द्रव की श्यानता के कारण अवमंदन को नगण्य मानिए ) |02:55View Solutionआधार क्षेत्रफल A तथा ऊंचाई के h एक कॉर्क का बेलनाकार टुकड़ा pl घनत्व के किसी द्रव में तैर रहा है । कॉर्क को थोड़ा नीचे दबाकर स्वतंत्र छोड़ देते है , यह दर्शाइये कि कॉर्क ऊपर - नीचे सरल आवर्त दोलन करता है जिसका आवर्तकाल T=2π√hpplg है ।
यहाँ ρ कॉर्क का घनत्व है ( द्रव कि श्यानता के कारण अवमन्दन को नगण्य मानिए ।)07:28View Solutionआधार क्षेत्रफलA तथा ऊँचाई h के कॉर्क का बेलनाकार टुकड़ा ρ1 घनत्व के किसी द्रव पर तैर रहा है। कॉर्क को थोड़ा नीचे दबाकर स्वतंत्र छोड़ देते है , यह दर्शाइए की कॉर्क ऊपर - नीचे सरल आवर्त दोलन करता है जिसका आवर्त T=2v√hρρ1g है।
यहाँ ρ कॉर्क का घनत्व है (द्रव की श्यानता के कारण अवमंदन को नगण्य मानिए)View SolutionA cylindrical piece of cork of density rho , base area A and height h, floats in a liquid of density rho_(1) . The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically, with a period T=2pisqrt((hrho)/(rho_(1)g)) , where 'rho' is the density of the cork.
View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density p1. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hpp1g
where p is the density of cork. (Ignore damping due to viscosity of the liquid).08:27View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density pl. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hpp1g
where p is the density of cork. (Ignore damping due to viscosity of the liquid).View SolutionA cylindrical piece of cork of base area A and height h floats in a liquid of density rho_(1) . The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period T=2pisqrt((hrho)/(rho_(1)g))
View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density ρ1. The cork is depressed slightly and then released. The cork oscillates up and down simple harmonically with period is (ρ is the density of cork)
View Solution