A cylindrical piece of cork of base area A and height h floats in a liquid of density ρ1. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hρρ1g
To show that the cylindrical piece of cork oscillates up and down in simple harmonic motion (SHM) with a period given by
T=2π√hρρ1g,
we will follow these steps:
Step 1: Identify the parameters
Let:
- A = base area of the cork
- h = height of the cork
- ρ = density of the cork
- ρ1 = density of the liquid
- g = acceleration due to gravity
Step 2: Determine the mass of the cork
The mass m of the cork can be calculated using its density and volume:
m=ρ⋅V=ρ⋅(A⋅h)=A⋅h⋅ρ.
Step 3: Apply Archimedes' principle
When the cork is floating, the buoyant force Fb acting on it is equal to the weight of the liquid displaced by the submerged part of the cork. If y is the depth of the cork submerged in the liquid, then:
Fb=ρ1⋅(A⋅y)⋅g.
Step 4: Set up the equilibrium condition
At equilibrium, the buoyant force equals the weight of the cork:
Fb=m⋅g⟹ρ1⋅(A⋅y)⋅g=A⋅h⋅ρ⋅g.
This simplifies to:
ρ1⋅y=ρ⋅h.
Step 5: Consider the displacement
When the cork is depressed by a small distance x, the new submerged depth becomes y+x. The new buoyant force F′b is:
F′b=ρ1⋅(A⋅(y+x))⋅g=ρ1⋅(A⋅y)⋅g+ρ1⋅(A⋅x)⋅g.
Step 6: Calculate the restoring force
The restoring force F acting on the cork when it is displaced is given by:
F=F′b−mg=(ρ1⋅(A⋅(y+x))⋅g)−(A⋅h⋅ρ⋅g).
Substituting F′b:
F=ρ1⋅A⋅g⋅(y+x)−A⋅h⋅ρ⋅g.
Using the equilibrium condition ρ1⋅y=ρ⋅h:
F=ρ1⋅A⋅g⋅y+ρ1⋅A⋅g⋅x−ρ1⋅A⋅g⋅y=ρ1⋅A⋅g⋅x.
Thus, the restoring force can be expressed as:
F=−ρ1⋅A⋅g⋅x.
Step 7: Relate to SHM
This restoring force is proportional to the displacement x, indicating that the motion is simple harmonic. The effective spring constant k is given by:
k=ρ1⋅A⋅g.
Step 8: Calculate the period of oscillation
The period T of SHM is given by:
T=2π√mk.
Substituting m=A⋅h⋅ρ and k=ρ1⋅A⋅g:
T=2π√A⋅h⋅ρρ1⋅A⋅g=2π√h⋅ρρ1⋅g.
Thus, we have shown that the cork oscillates with a period:
T=2π√h⋅ρρ1⋅g.
Let:
- A = base area of the cork
- h = height of the cork
- ρ = density of the cork
- ρ1 = density of the liquid
- g = acceleration due to gravity
The mass m of the cork can be calculated using its density and volume:
m=ρ⋅V=ρ⋅(A⋅h)=A⋅h⋅ρ.
When the cork is floating, the buoyant force Fb acting on it is equal to the weight of the liquid displaced by the submerged part of the cork. If y is the depth of the cork submerged in the liquid, then:
Fb=ρ1⋅(A⋅y)⋅g.
At equilibrium, the buoyant force equals the weight of the cork:
Fb=m⋅g⟹ρ1⋅(A⋅y)⋅g=A⋅h⋅ρ⋅g.
This simplifies to:
ρ1⋅y=ρ⋅h.
When the cork is depressed by a small distance x, the new submerged depth becomes y+x. The new buoyant force F′b is:
F′b=ρ1⋅(A⋅(y+x))⋅g=ρ1⋅(A⋅y)⋅g+ρ1⋅(A⋅x)⋅g.
The restoring force F acting on the cork when it is displaced is given by:
F=F′b−mg=(ρ1⋅(A⋅(y+x))⋅g)−(A⋅h⋅ρ⋅g).
Substituting F′b:
F=ρ1⋅A⋅g⋅(y+x)−A⋅h⋅ρ⋅g.
Using the equilibrium condition ρ1⋅y=ρ⋅h:
F=ρ1⋅A⋅g⋅y+ρ1⋅A⋅g⋅x−ρ1⋅A⋅g⋅y=ρ1⋅A⋅g⋅x.
Thus, the restoring force can be expressed as:
F=−ρ1⋅A⋅g⋅x.
This restoring force is proportional to the displacement x, indicating that the motion is simple harmonic. The effective spring constant k is given by:
k=ρ1⋅A⋅g.
The period T of SHM is given by:
T=2π√mk.
Substituting m=A⋅h⋅ρ and k=ρ1⋅A⋅g:
T=2π√A⋅h⋅ρρ1⋅A⋅g=2π√h⋅ρρ1⋅g.
T=2π√h⋅ρρ1⋅g.
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Additional Exercises
6 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - NCERT CHAPTER
26 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Advanced Problems For Competitions
20 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
Similar Questions
A cylidrical wooden piece of cork floats in a liquid of density σ. The cork is depressed slightly and released. Show that the cork will oscillate up and down simple harmonicaly with a period.
T=2π√ρhσg, where ρ is the density of the cork.
View SolutionA block of ice with an area A and a height h floats in water of density ρ0. What work should be performed to submerge the ice block completely into water if density of ice is ρ1 ?
View Solution
Knowledge Check
A solid cube of side a and density ρ0 floats on the surface of a liquid of density ρ. If the cube is slightly pushed downward, then it oscillates simple harmonically with a period of
A2π√ρ0ρagB2π√ρρ0agC2π ⎷a(1−ρρ0)gD2π ⎷a(1+ρρ0)gA cylindrical of wood (density =600kgm−3) of base area 30cm2 and height 54cm, floats in a liquid of density 900kg−3 The block is deapressed slightly and then released. The time period of the resulting oscillations of the block would be equal to that of a simple pendulum of length (nearly) :
A26cmB52cmC36cmD65cmA rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
AT∝√ρBT∝1√ACT∝1ρDT∝1√m
A plank of mass 'm' and area of cross - section A is floating in a non - viscous liquid of desity ρ. When displaced slightly from the mean position, it starts oscillating. Prove that oscillations are simple harmonic and find its time period.
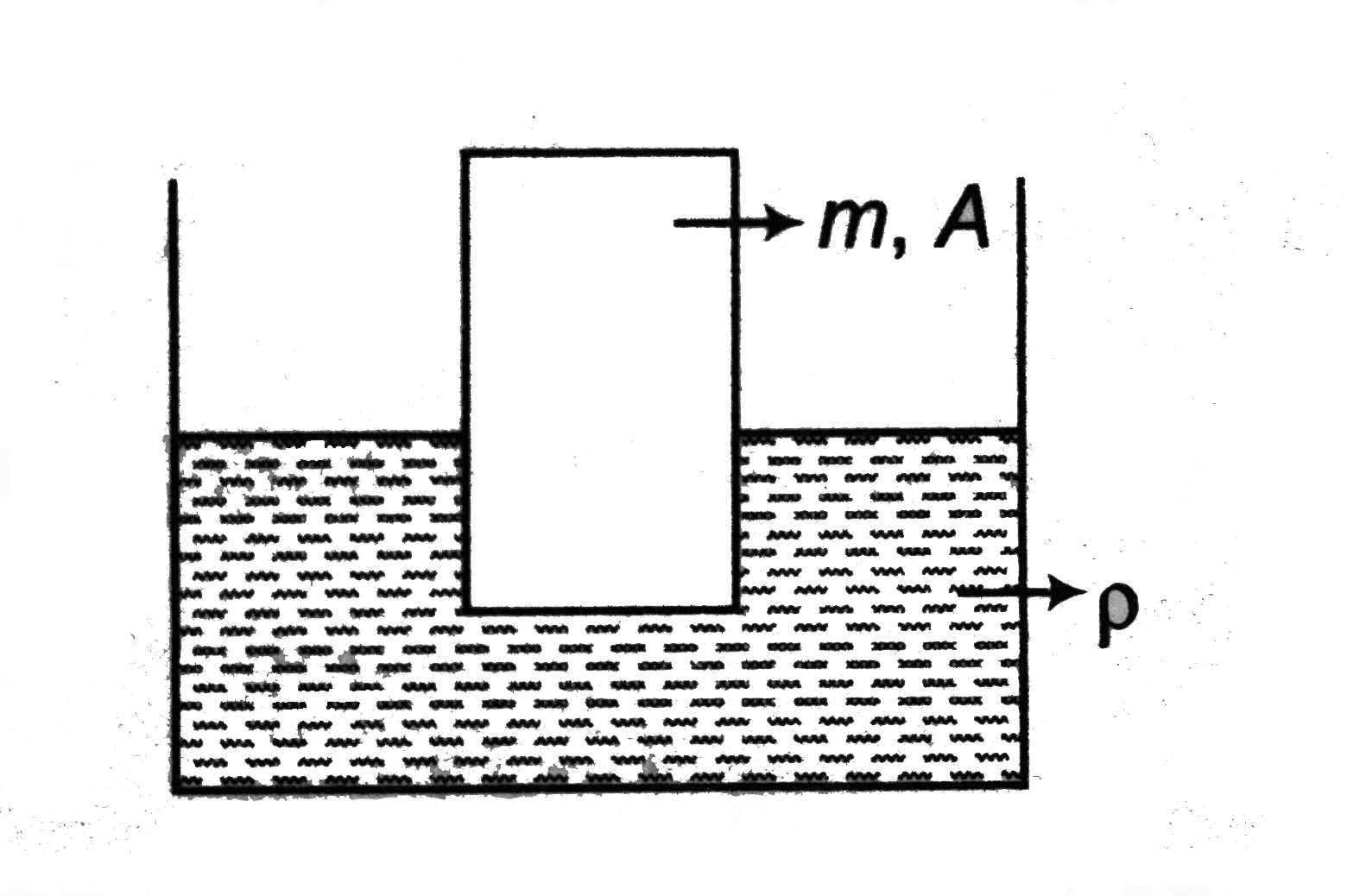
View SolutionA cylinderical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that the log would execute S.H.M. with a tiem period.
T=2π√mAρg where m is mass of the body and ρ is density of the liquid.
View SolutionA cylindrical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that lon would execute SHM with a time period. T=2π√mApg where, m is mass of the body and p is density of the liquid.
View SolutionA wooden cube (density of wood ρ3 ') of side l 'floats in a liquid of density ' ρ with its upper and lower surfaces horizontal. If the cube is pushed slightly down and released, it performs simple harmonic motion of period T. Then, T is equal to 2π√xlyg. Find (x+y).
View SolutionA vertical U tube contains a liquid of density ρ, length of the liquid in the tube is 2H. The liquid is displaced slightly and released. Show that the liquid will execute SHM. Also find its time period. Take liquid to be ideal.

View Solution
