A person normally weighing 50kg stands on a massless platform which oscillates up and down harmonically at a frequency of and an amplitude . A weighing machine on the platform gives the persons weight against time.
If answer of part (1) is yes, what will be the maximum and minimum reading in the machine and at which position?Solution in Gujrati
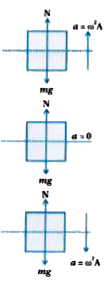
Here, oscillations are periodic hence acceleration changes. The weight of man depend on direction of acceleration and its magnitude in up and down motion.
(b) The acceleration is maximum at two extreme points of the platform.
At upper extreme point acceleration on platform is in downward,
From equation of motion
Weight = 96N and at mean position
Weight = 490 N
At lower extreme point,
Weight = 884 N.
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-E (MCQs ASKED IN GUJARAT BOARD AND COMPETITIVE EXAMS)66videos
OSCILLATIONS
- BOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-F (QUESTIONS FROM MODULE SIMPLE QUESTIONS)20videos
OSCILLATIONS
- BOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-D (NCERT EXEMPLAR SOLUTION SHORT ANSWER QUESTIONS)6videos
OSCILLATIONS
- BOOK - KUMAR PRAKASHANCHAPTER - OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE EXERCISE - CHAPTER - 8 (Match Type questions)5videos
OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE
- BOOK - KUMAR PRAKASHANCHAPTER - PHYSICAL WORLDEXERCISE - SECTION-E (QUESTIONS FROM MODULE)9videos
PHYSICAL WORLD
Similar Questions
A particle executes SHM along X-axis. The force acting on it is given by……….
05:10View SolutionA particle executes simple harmonic motion with an amplitude A. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude form the equilibrium position is………..
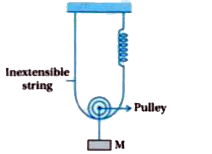
06:04View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
 .02:59View Solution
.02:59View SolutionType of satellites are given in Column-I and their uses are given in Column-II. Match them properly :
Column-IColumn-II(1) Polar satellite(a) Tele communication(2) Geo-stationary satellite(b) Investigation(c) For information about atmosphere05:47View Solution.…. state of substance at very high temperature has generated hope of energy source for mankind.
08:15View SolutionA person normally weighing 60 kg stands on a plateform which oscillates up and down har monically at a frequency 2.0 sec^(-1) and an amplitude 5.0 cm . If a machine on the plateform gives the person's weight against time deduce the maximum and minimum reading it will shown, Take g = 10 m//sec^(2) .
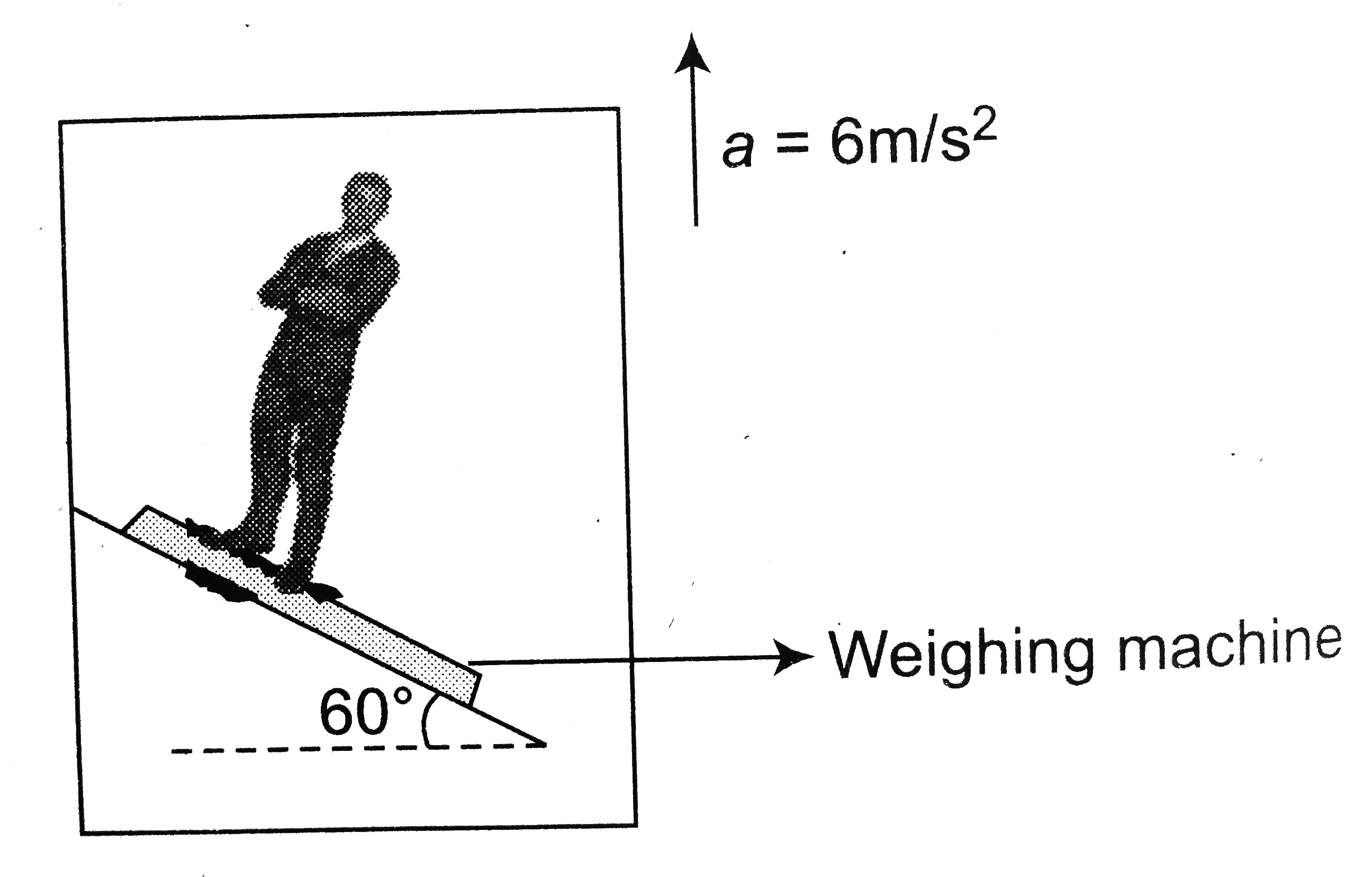
03:07View SolutionAn elevator is accelerating upwards with an acceleration of 6m/s2 . Inside it a person of mass 50kg is standing on a weighing machine which is kept on an inclined plane having angle of inclination 60∘ . The reading of the weighing machine is:
 06:28View Solution
06:28View SolutionA man stands on a weighing machin palced on a horizontal platform the machine reads 50kg. By mean of a suitable mechanism, the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibration per second. What will be the effect on the readin of the weighing machin? Teh amplitude of vibration of platform is 5cm. Take g=10ms−1
01:36View SolutionA perosn normally weighting 50kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0s^(-1) and an amplitude 5.0 cm. A weighing machine on the platform gives the persons weight against time. (a) Will there be any in weight of body , during the oscillation? (b) If answer to part (a) is yes, what will be the maximum and minimum readin in the machine and at which position?
01:56View SolutionPassage XIII) Mr. Anoop having mass 50 ks is standing on a massless platform which oscillates up and down (doing SHM) of frequency 0.5 sec^(-1) and amplitude 0.4m. Platforms has a weightng machine fitted in it (Which is also massless). On which Anoop is standing. (Take (pi^(2)) = 10 and g = 1- m//s^(2) . Assume that at t=0 (Platform+Anoop) is at their highest point of oscillation. [More than one option is correct] Which of the following will be correct for reading of weighting machine
08:02View SolutionA person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0s^(-1) and an amplitude 5.0 cm. A weighing machine on the platform gives the persons wieght against time. (a) Will there be any change in weight of the body, during the oscillation? (b) If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?
02:12View SolutionA man is standing on a platform moving up and down as a S.H.M. will there be any change in his weight as recorded by a weighing machine on the platform ?
06:47View SolutionA man is standing on a platform moving up and down as a S.H.M. will there be any change in his weight as recorded by a weighing machine on the platform ?
07:08View Solutionएक व्यक्ति दरवाजे के पास रखी तौलने वाली मशीन पर खड़ा है । तौलने वाली मशीन के पाठ्यांक में क्या परिवर्तन होगा यदि व्यक्ति -
( ii ) शटर को नीचे खींचता है ?06:38View SolutionA boy is standing on a weighing machine placed on a horizontal platform. The reading of weighing machine is 70 kg. Using a suitable mechanism the platform is made to execute harmonic vibrations with a frequency of 1 vibration per second. Calculate the maximum and minimum force exerted on the boy if the amplitude of vibration of platform is 6 cm.
03:57View Solution

