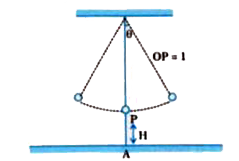
A simple pendulum of time period 1s and length l is hung from a fixed support at 0. Such that the bob is at a distance H vertically above A on the ground (figure) the amplitude is θ0 the string snaps at θ=θ02. Find the time taken by the bob to hit the ground. Also find distance from A where bob hits the ground. Assume θ0 to be small, so that sinθ0≈θ0 andcosθ0≈1.
 .Solution in Gujrati
.Solution in Gujrati
Two components of velocity
Perpendicular component to the string vy=lωsinθ02
Prallel component to the string vx=lωcos(θ0)2
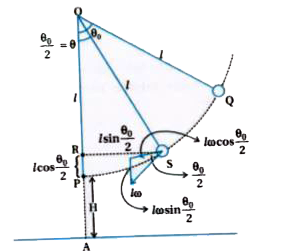
From v=rω
∴v=lω
Suppose at t=0,θ=θ0
∴θ=θ0cosωt
but T=1s,∴ω2πT=2πrad/s
∴θ=θ0cos2πt ........(1)
Now at t=t1 time, θ=θ02
∴θ02=θ0cos2πt1
∴12=cos2πt1
∴2πt1=π3
∴t1=16s
Difference equation (1) with time,
dθdt=−θ02πsin2πt
∴t=t1 time
ω=−2πθ0×sin2π×16
=−2πθ0×sinπ3
=−2πθ0×sin√33
∴ω=−√3πθ0
(-)ve shows that bob.s motion is towards, left. Since linear velocity is in the tangential direction.
∴v=lω [∴v=Aω]
∴v=−√3πθ0l
The Y-component of linear velocity
vy=−√3πθ0lsinθ02 and x-component of velocity
vx=−√3πθ0lcosθ02
When string break, the height of bob from the ground,
H.=H+l(1−cosθ02) ........(2)
Time taken by the bob from this height (when string break) to ground it t, then
H.=vyt+12gt2 (all terms are (-)ve)
∴12gt2+√2πθ0lsinθ02l−H.=0 is a quadratic formula of t
∴△=b2−4ac
=3p2θ20sin2θ02+4×12g×H.
=3π2θ20l2sin2θ02+2gH.
but θ0 is small ∴sin2θ02=0, △=2gH.
∴√△=√2gH.
∴t=−b±√△2a
=−√3πθ0lsinθ02±√2gH.2×12g
but sinθ02=0,
t=±√2gH.g
∴t=√2H.g ........(3)
Now, in H.=H+l(1−cosθ02),θ0 is small cosθ22≈1
∴H.=H+l(1−1)
∴H.=H
∴t=√2Hg [ from equation (3) ] .........(4)
The bob covered distance in horizontal direction.
X=vxt
=−√3πθ0lcosθ02×t
Since θ0 is small, cosθ02≈1 and taking t=√2Hg,
X=−√3πθ0l×√2Hg
∴X=−√6Hg×πθ0l ........(5)
but string breaks, the bob is at RS distance from vertical at that time and RS=lsinθ02
RS=lθ02 [∴sin(θ0)2≈θ02]
When bob hit at ground, the distance from bob at that time
=lθ02+X
=lθ02−√6Hgπθ0l
=θ0l(12−π√6Hg).
Topper's Solved these Questions
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-E (MCQs ASKED IN GUJARAT BOARD AND COMPETITIVE EXAMS)
66 Videos
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-F (QUESTIONS FROM MODULE SIMPLE QUESTIONS)
20 Videos
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-D (NCERT EXEMPLAR SOLUTION SHORT ANSWER QUESTIONS)
6 Videos
- OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE BOOK - KUMAR PRAKASHANCHAPTER - OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE EXERCISE - CHAPTER - 8 (Match Type questions)
5 Videos
- PHYSICAL WORLDBOOK - KUMAR PRAKASHANCHAPTER - PHYSICAL WORLDEXERCISE - SECTION-E (QUESTIONS FROM MODULE)
9 Videos
Similar Questions
A particle executes SHM along X-axis. The force acting on it is given by……….
View SolutionA particle executes simple harmonic motion with an amplitude A. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude form the equilibrium position is………..
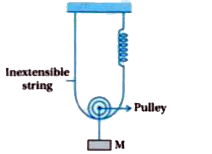
View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
 .
.
View SolutionType of satellites are given in Column-I and their uses are given in Column-II. Match them properly :
Column-IColumn-II(1) Polar satellite(a) Tele communication(2) Geo-stationary satellite(b) Investigation(c) For information about atmosphere
View Solution.…. state of substance at very high temperature has generated hope of energy source for mankind.
View SolutionSuppose the amplitude of a simple pendulum having a bob of mass m is θ0. Find the tension in the string when the bob is at its extreme position.
View SolutionA pendulum of length l=1m is released from theta_(0)=60^(@) . The rate of change of speed of the bob at theta=30^(@) is.
View SolutionA simple pendulum of time period 1s and length l is hung from a fixed support at 0. Such that the bob is at a distance H vertically above A on the ground (figure) the amplitude is θ0 the string snaps at 0=θ0/2. Find the time taken by the bob to hit the ground. Also find distance from A where bob hits the ground. Assume θ0 to be small, so that sinθ0≈θ0andcosθ0≈1.

View Solution(i) A simple pendulum consist of a small bob of mass m tied to a string of length L. Show that the total energy of oscillation of the pendulum is E≅12mgLθ20 when it is oscillating with a small angular amplitude θ0. Assume the gravitational potential energy to be zero of the lowest position of the bob. (ii) Three identical pendulums A, B and C are suspended from the ceiling of a room. They are swinging in semicircular arcs in vertical planes. The string of pendulum A snaps when it is vertical and it was found that the bob fell on the floor with speed V1. The string of B breaks when it makes an angle of 30° to the vertical and the bob hits the floor with speed V2. The string of pendulum C was cut when it was horizontal and the bob falls to the floor hitting it with a speed V3. Which is greatest and which is smallest among V1,V2 and V3?
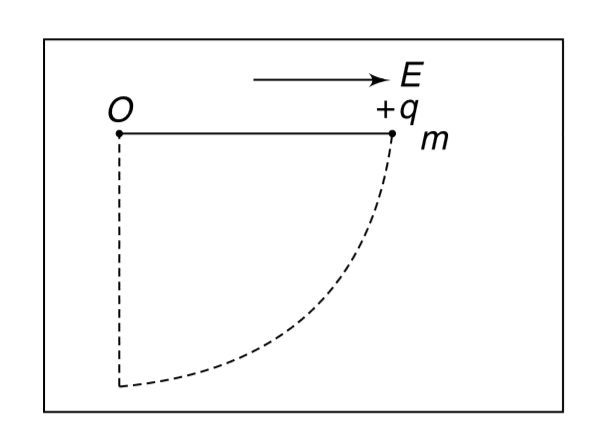
View SolutionThere is a uniform horizontal electric field of strength E in a region. A pendulum bob is pulled to make the string horizontal and released. The bob has mass m and charge q. (a) Find the maximum angle (θ0) that the bob swings before coming to rest momentarily. (b) Find E if the bob comes to rest when the string is vertical.
View SolutionA pendulum bob of mass m and length L is released from angle theta with the vertical. Find (a) the speed of the bob at the bottom of the swing and (b) tension in the string at that time
View SolutionA simple pendulum of time period 1s and length l is hung from a fixed support at 0. Such that the bob is at a distance H vertically above A on the ground (figure) the amplitude is theta_(0) the string snaps at 0=theta_(0)//2. Find the time taken by the bob to hit the ground. Also find distance from A where bob hits the ground. Assume theta_(0) to be small, so that sintheta_(0)~~theta_(0)and costheta_(0)~~1.
View SolutionA pendulum of length l = 1m is released from θ0=60∘. The rate of change of speed of the bob at θ=30∘ is (g=10m/s2)
View Solutionएक सरल दोलक के बॉब का द्रव्यमान m है तथा वह आयाम θ0 के साथ दोलन कर रहा है। (a) जब ऊर्ध्वाधर से कोणीय विस्थापन θ है उस समय डोरी में तनाव T ज्ञात करे। (b) डोरी में अधिकतम तथा न्यूनतम तनाव के मान निकालें।
View SolutionThe bob of simple pendulum is hanging vertically down from a fixed identical bob by means of a string of length l. If both bobs are charged with a charge q each, time period of the pendulum is (ignore the radii of the bobs)
View Solution
