Supposing Newton's Law of gravitation for gravitation forces F1andF2 between two masses my and m, at positions r1andr2 read F1=−F2=−r12r123GM20(m1m2M20)2
where M0 is a constant of dimension of mass,r12=r1−r2 and n is a number. In such a case, Solution in Gujrati
the acceleration due to gravity on the earth will be different for different objects
none of the three laws of Kepler will be valid
only the third law will become invalid
for n negative, an object lighter than water will sink in water
The correct Answer is:A, C, D
Given F1=−F2=−r12r312GM20(m1m2M20)n
r12=r1−r2
Acceleration due to gravity,
g=|F|mass
=GM20(m1m2)nr212(M0)2n×1(mass)
Here, g is not constant , hence constant of proportionality will not be constant in Kepler.s third law . Hence , Kepler.s third law will be invalid But, first two Kepler.s laws will be valid.
For negative, n g = GM20(m1m2)nr212(M0)−2n×1(mass)
=GM2(1=1)00(m1m2)−nr212 (mass)
g=GM20r212(M20m1m2)n×1(mass)
Here, M0>m1 or m2. So that g>0 , hence is this case situation will reverse i.e. object lighter than water will sink in water.
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - GRAVITATIONEXERCISE - Section - D NCERT Exemplar Solutions (MIultiple Choice Questions (More than one options) )1videos
GRAVITATION
- BOOK - KUMAR PRAKASHANCHAPTER - GRAVITATIONEXERCISE - Section - D NCERT Exemplar Solutions (Very Short Answer Type Question )11videos
GRAVITATION
- BOOK - KUMAR PRAKASHANCHAPTER - GRAVITATIONEXERCISE - Section - C Objective Questions (VSQs)80videos
GRAVITATION
- BOOK - KUMAR PRAKASHANCHAPTER - LAW OF MOTIONEXERCISE - (QUESTION PAPER) SECTION-D1videos
LAW OF MOTION
Similar Questions
Which of the following options are correct?
03:19View SolutionMolecules in air in the atmosphere are attracted by gravitational force of the earth. Explain why all of them do not fall into the earth just like an apple falling from a tree.
02:13View SolutionDefine acceleration due to gravity.
02:13View SolutionA 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed ?
03:48View SolutionThe magnitude of the gravitational field at distance r1andr_2omthecentreofaunifromsphereofradiusRandmassmareF_1 and F_2 respectively. Then:
04:24View SolutionSupposing Newton's law of gravitation for gravitation force F1 and F2 between two masses m1 and m2 at positions r1 and r2 read F2=−F2=r12r312GM20(m1m2M20)n where M0 is a constant dimension of mass, r12=r1−r2 and n is number. In such a case.
08:12View SolutionSupposing Newton's law of gravitation for gravitation force F1 and F2 between two masses m1 and m2 at positions r1 and r2 read F2=−F2=r12r312GM20(m1m2M20)n where M0 is a constant dimension of mass, r12=r1−r2 and n is number. In such a case.
03:21View SolutionSupposing Newton's law of gravitation for gravitation forces F_(1) and F_(2) between two masses m_(1) and m_(2) at positions r_(1) and r_(2) read where M_(0) is a constant of dimension of mass, r_(12) = r_(1) - r_(2) and n is a number. In such a case,
08:48View SolutionThe resistance of metal sheet 1 between A and B is R1 and the resistance of sheet 2 between A' and B' is R2. The value of the ratio R1R2 is
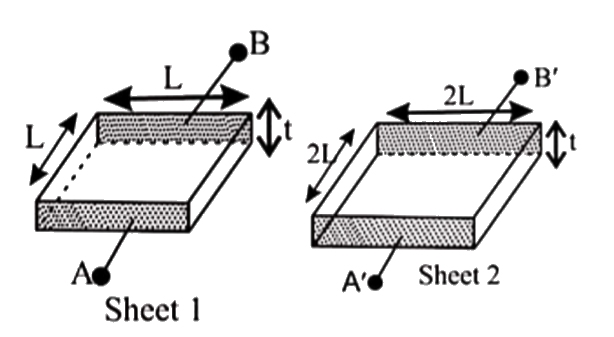 04:49View Solution
04:49View SolutionThe radius of a uniform sphere is R and its mass is M. The values of the gravitational intensity at distance r_1 and r_2 from the centre of the sphere are F_1 and F_2 respectively. Then,
04:49View Solutionযদি rr1+loger2r1=1 এবং r2=erহয়, তবে দেখাও যে,r1rloger1r=1।
08:35View SolutionSupposing Newton's law of gravitation for gravitation forces F1 and F2 between two masses m1 and m2 at positions r1 and r2 read
where M0 is a constant of dimension of mass, r12=r1−r2 and n is a number. In such a case,01:58View SolutionThe magnitudes of the gravitational fields at distances r1 and r2 from the centre of a uniform sphere of radius R and mass M are F1 and F2 respectively then
(a)F1F2=r1r2 if r1<R and r2<R
(b)F1F2=(r2r1)2 if r1>R and r2>R
(c)F1F2=r1r2 if r1>R and r2>R
(d)F1F2=(r1r2)2 if r1<R and r2<RView SolutionThe magnitudes of the gravitational fields at distances r1 and r2 from the centre of a uniform sphere of radius R and mass M are F1 and F2 respectively then
(a)F1F2=r1r2 if r1<R and r2<R
(b)F1F2=(r2r1)2 if r1>R and r2>R
(c)F1F2=r1r2 if r1>R and r2>R
(d)F1F2=(r1r2)2 if r1<R and r2<R02:57View Solutionमान लीजिये r1 और r2 पर स्थित दो द्रव्यमानो m1 तथा m2 के बीच गुरुत्वाकर्षण बलों F1 तथा F2 के लिए न्यूटन के गुरुत्वाकर्षण नियम को F1=−F2=−r12r312GM20(m1m2M20)n द्वारा व्यक्त किया जाता है। यहाँ M0 एक स्थिरांक है जिसकी विमा द्रव्यमान की है। r12=r1−r2 तथा n कोई संख्या है। ऐसे प्रकरण में
07:46View Solution

