The magnitude of the gravitational field at distance r1andr_2omthecentreofaunifromsphereofradiusRandmassmareF_1 and F_2 respectively. Then:
F1F2=r1r2 if r1<R and r2<R
F1F2=r22r21 if r1>R and r2>R
F1F2=r1r2 if r1>R and r2>R
F1F2=r21r22 if r1<R and r2<R
The correct Answer is:A, B
To solve the problem, we need to analyze the gravitational field at two different distances r1 and r2 from the center of a uniform sphere of radius R and mass m. The gravitational field F at a distance r from the center of a sphere can be described using the following principles:
1. Inside the Sphere (r < R): The gravitational field is given by:
F=GmR3r
where G is the gravitational constant, m is the mass of the sphere, and R is the radius of the sphere.
2. Outside the Sphere (r ≥ R): The gravitational field behaves like that of a point mass located at the center of the sphere:
F=Gmr2
Step 1: Determine the conditions for r1 and r2
- We need to consider two cases based on the values of r1 and r2 in relation to R:
- Case 1: Both r1<R and r2<R
- Case 2: Both r1≥R and r2≥R
Step 2: Case 1 - Both r1 and r2 are less than R
- For r1<R:
F1=GmR3r1
- For r2<R:
F2=GmR3r2
- Now, we can find the ratio F1F2:
F1F2=GmR3r1GmR3r2=r1r2
Step 3: Case 2 - Both r1 and r2 are greater than or equal to R
- For r1≥R:
F1=Gmr21
- For r2≥R:
F2=Gmr22
- Now, we can find the ratio F1F2:
F1F2=Gmr21Gmr22=r22r21
Conclusion:
- The correct relationship for the gravitational fields depends on whether both distances are inside or outside the sphere.
- If both r1 and r2 are less than R, then F1F2=r1r2.
- If both r1 and r2 are greater than or equal to R, then F1F2=r22r21.
F=GmR3r
where G is the gravitational constant, m is the mass of the sphere, and R is the radius of the sphere.
F=Gmr2
- Case 1: Both r1<R and r2<R
- Case 2: Both r1≥R and r2≥R
F1=GmR3r1
- For r2<R:
F2=GmR3r2
- Now, we can find the ratio F1F2:
F1F2=GmR3r1GmR3r2=r1r2
F1=Gmr21
- For r2≥R:
F2=Gmr22
- Now, we can find the ratio F1F2:
F1F2=Gmr21Gmr22=r22r21
- If both r1 and r2 are less than R, then F1F2=r1r2.
- If both r1 and r2 are greater than or equal to R, then F1F2=r22r21.
Topper's Solved these Questions
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive)ASSERTIOIN AND REASON
Explore 1 Video
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive)MATCH MATRIX
Explore 1 Video
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) SINGLE OPTION CORRECT
Explore 14 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:JEE Advanced ( ARCHIVE LEVEL-2)
Explore 12 Videos
Similar Questions
The magnitude of the gravitational field at distance r1 and r2 from the centre of a uniform sphere of radius R and mass M are F1 and F2 respectively. Then:
View SolutionThe magnitude of gravitational field at distances r1 and r2 from the centre of a uniform sphere of radius R and mass M, respectively. Find the ratio of (I1)/(I2)) if r1>R and r2>R.
View Solution
Knowledge Check
The correct plot of the magnitude of magnetic field →B vs distance r from centre of the wire is, if the radius of wire is R
A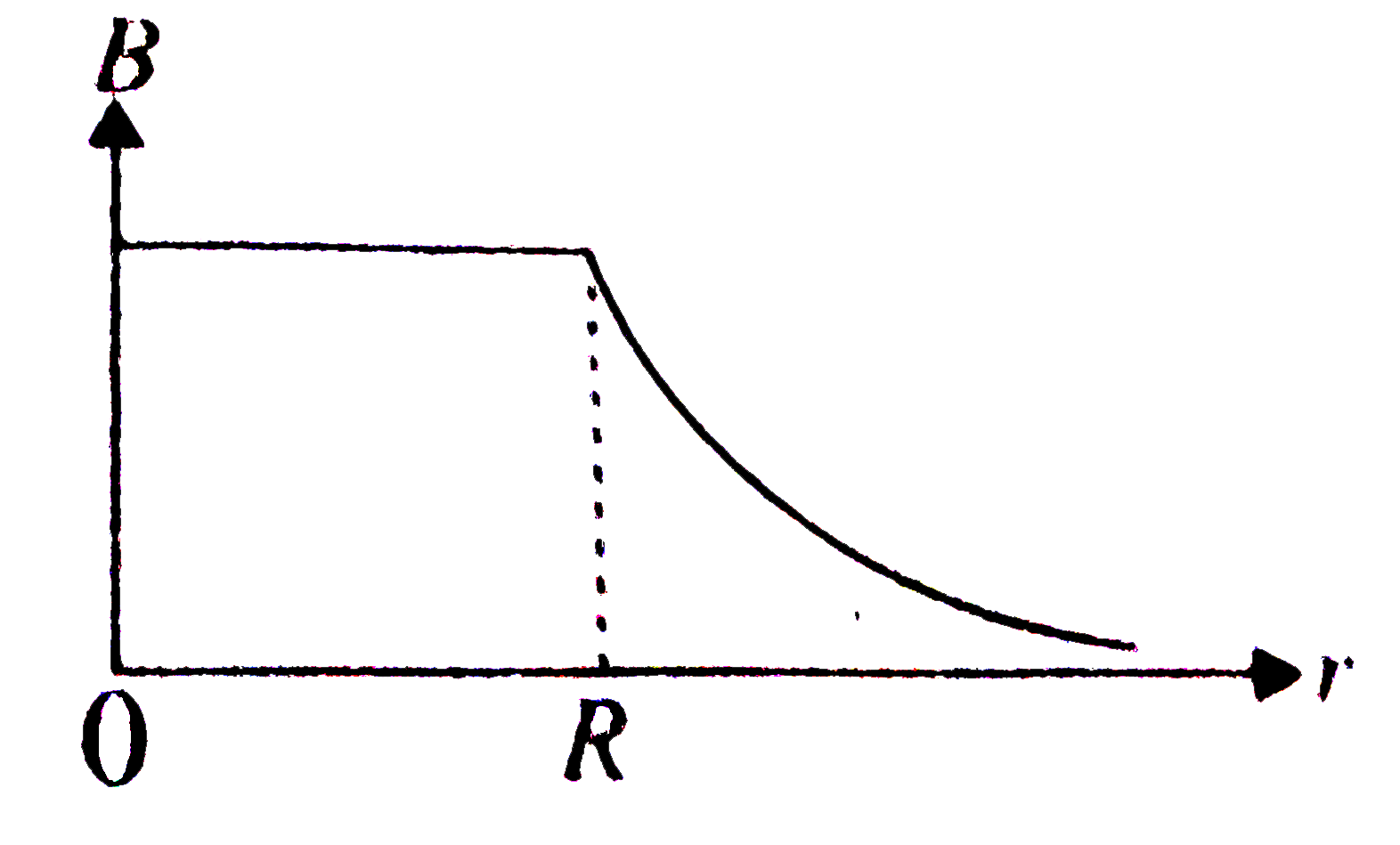 B
B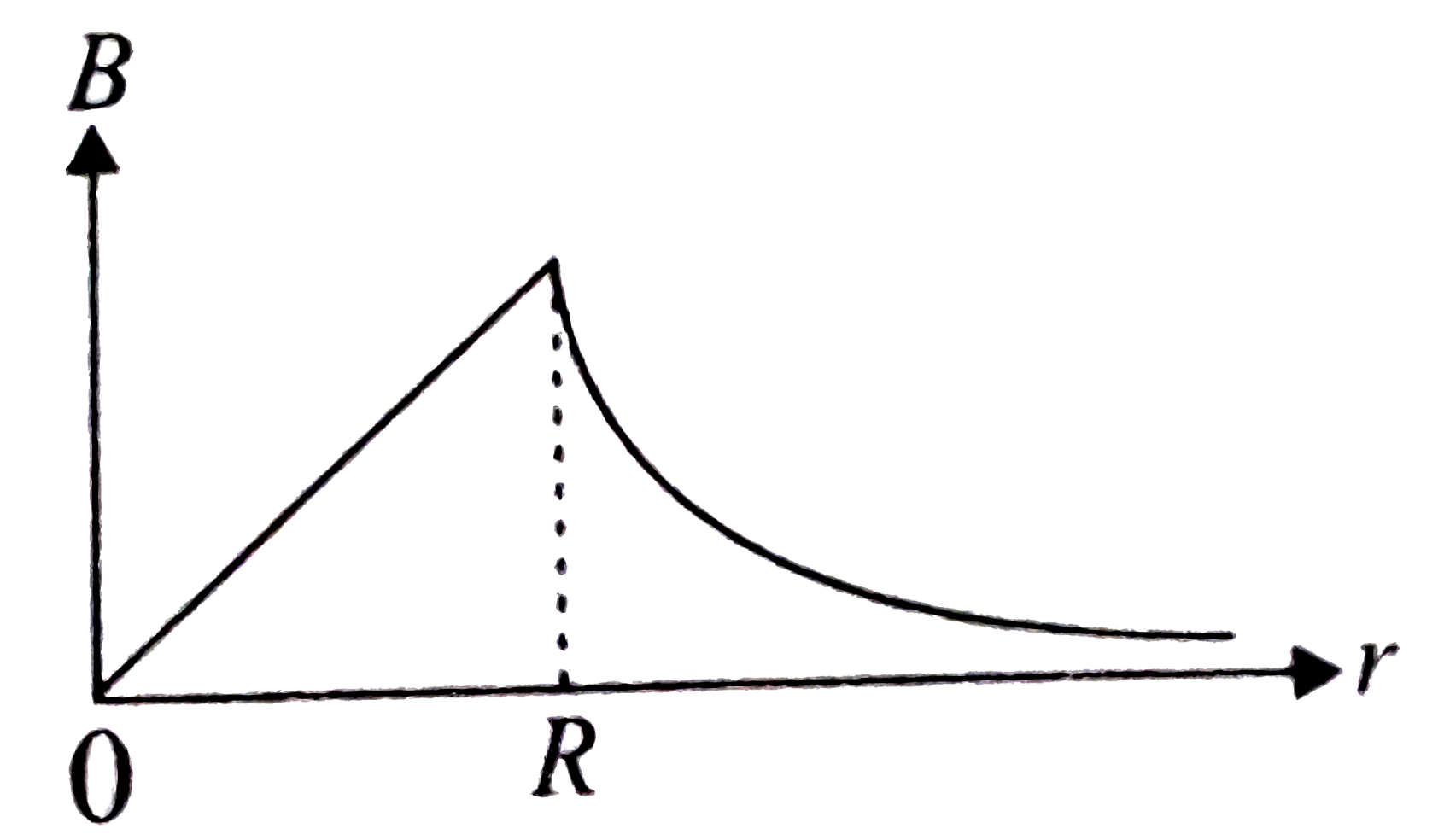 C
C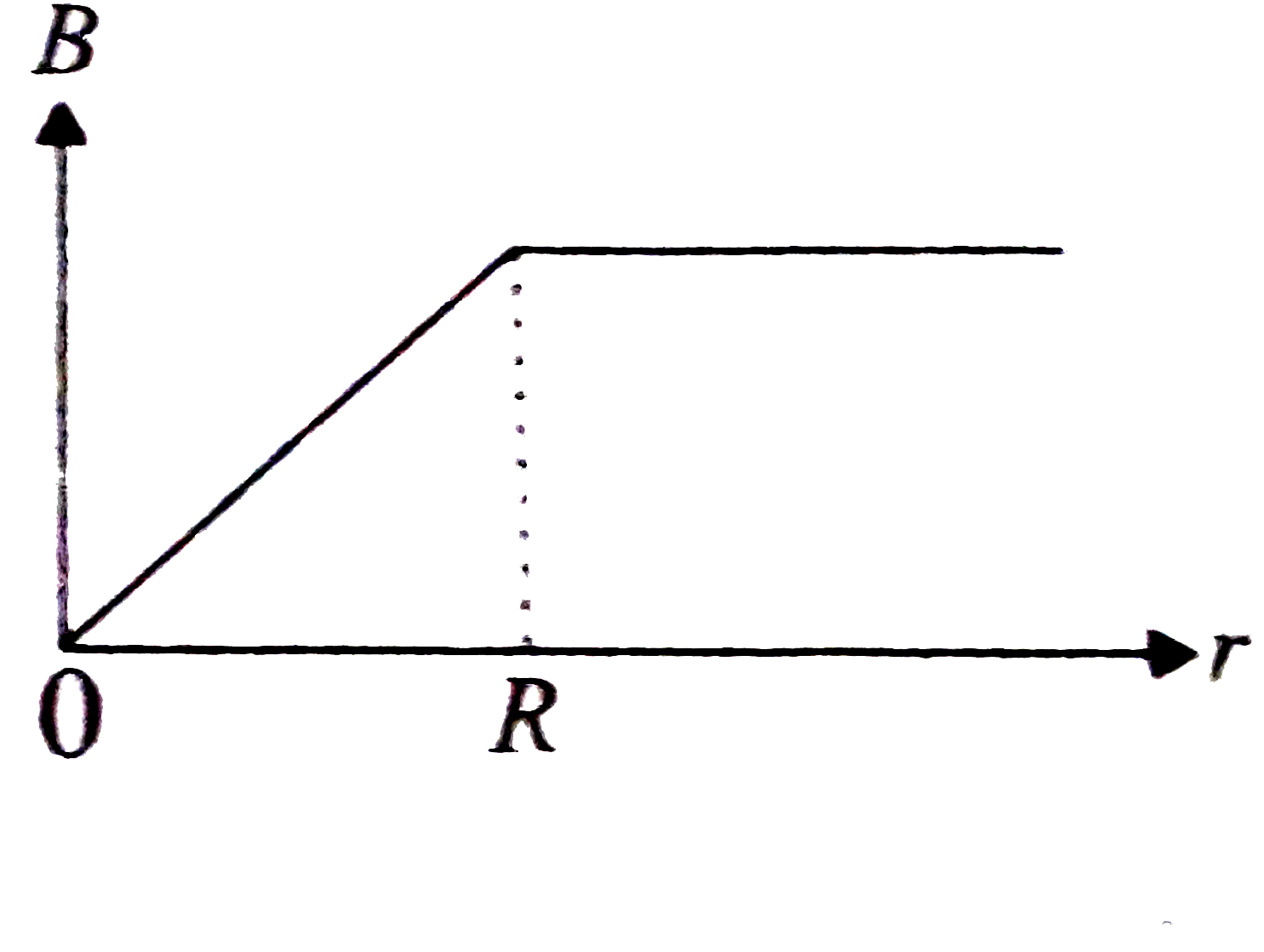 D
D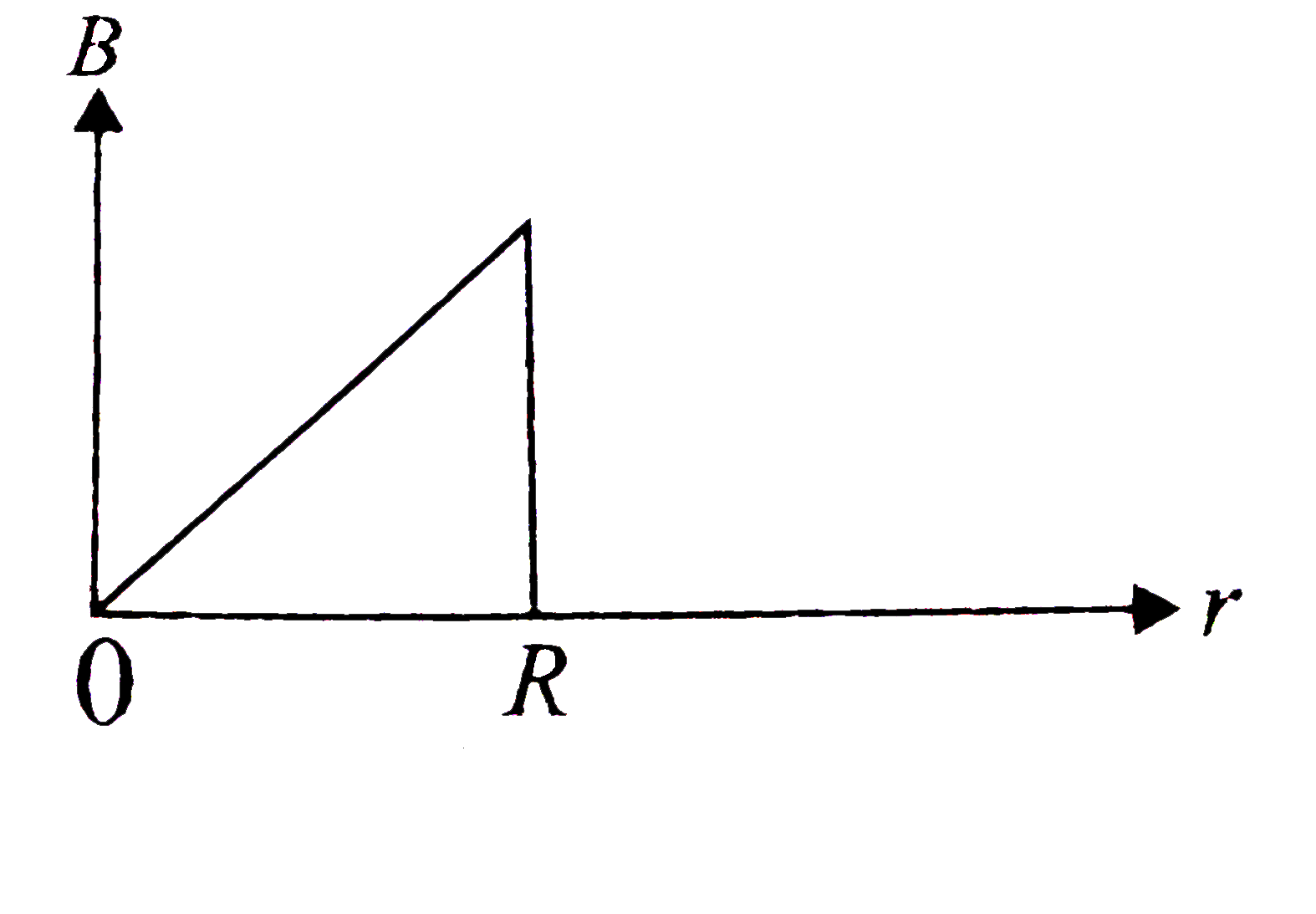
Let E1andE2 denotes gravitational field at distance r1andr2 from the axis of an infinitely long solid cylinder of the radius R. Which of the following must hold true ?
View SolutionCalculate the gravitational field intensity and potential at the centre of the base of a solid hemisphere of mass m, radius R
View SolutionThe gravitational potential energy of a body at a distance r from the centre of earth is U. Its weight at a distance 2r from the centre of earth is
View SolutionThe gravitational potential at a point outside the solid sphere of radius "R" and at a distance of "r" will be :
View SolutionCalculate the gravitational field intensity at the centre of the base of a hollow hemisphere of mass M and radius R. (Assume the base of hemisphere to be open)

View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]
View Solution
