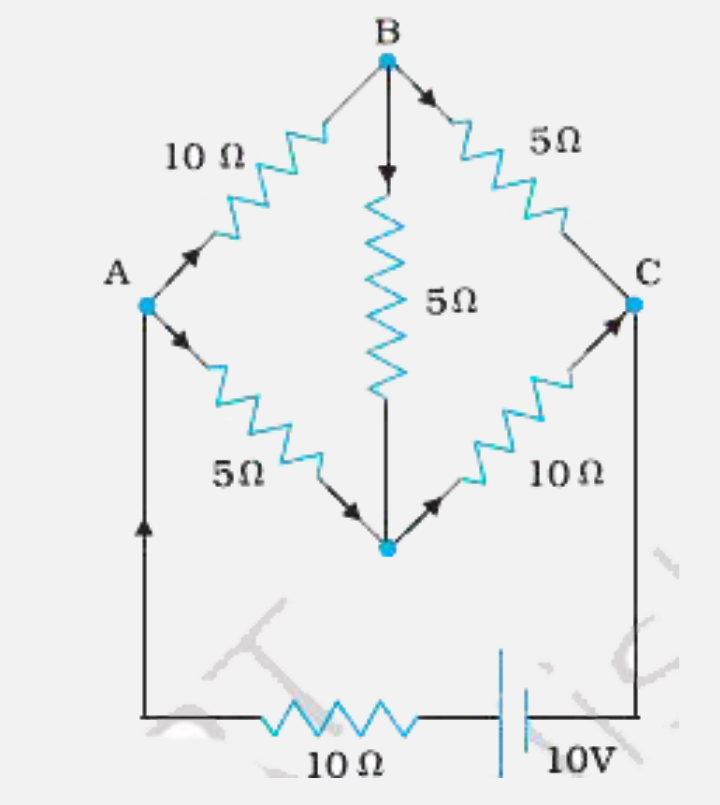
Determine the current in each branch of the given network.
 Solution in Gujrati
Solution in Gujrati
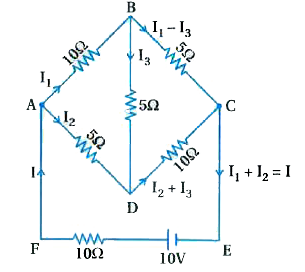
In above circuit, we have to find currents in different branches.
Applying KVL in the closed path ABDA,
−10I1−5I3+5I2=0
∴10I1=5I2−5I3
∴2I1=I2−I3 ... (1)
Applying KVL in the closed path BCDB,
−5(I1−I3)+10(I2+I3)+5I3=0
∴5I1=20I3+10I2
∴I1=2I2+4I3
∴2I1=4I2+8I3 .... (2)
From equation (1) and (2),
I1−I3=4I2+8I3
∴3I2=−9I3
∴I2=−3I3 ... (3)
From equation (1) and (3),
2I1=−3I3=−4I3
∴I1=−2I3 .... (4)
Applying KVL in the closed path ADCEFA , we get,
−5I2−10(I2+I3)−10t=−10
∴15I2+10I3+10I=10
∴15I2+10I3+10(I1+I2)=10
∴10I1+25I2+10I3=10
∴10(−2I3)+25(−3I3)+10I3=10
∴−85I3=10
∴I3=−1085=−217A ... (5)
From equation (4) and (5).
From equation (4) and (5) ,
I1=−2(−217)=417A ... (6)
From equation (3) and (5)
I2=−3(−217)=617A .... (7)
now ,
I=I1+I2=417+617=1017A ....(8)
From equation (5) ,
|I3|=217 A
(Direction of I3 will be opposite to the direction shown in the figure ).
Final answer :
(i) Current in branch AB is,
I1=417A
(ii) Current in branch BC is,
I1−I3=417−(−217)=617A
(iii) Current in branch CD is,
I2+I3=617+(−217)=417 A
(iv) Current in branch DA is,
I2=617A
(v) Current in branch BD is,
|I3|=217A (Direction will be from D to B)
(vi) Current in branch FE is,
I = 1017A
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - KUMAR PRAKASHANCHAPTER - CURRENT ELECTRICITYEXERCISE - SECTION [B] (NUMERICAL FROM .DARPAN. BASED ON TEXTBOOK)
13 Videos
- CURRENT ELECTRICITYBOOK - KUMAR PRAKASHANCHAPTER - CURRENT ELECTRICITYEXERCISE - SECTION [B] (NUMERICAL)
10 Videos
- CURRENT ELECTRICITYBOOK - KUMAR PRAKASHANCHAPTER - CURRENT ELECTRICITYEXERCISE - SECTION [B] NUMERICALS (NUMERICAL FROM TEXTUAL ILLUSTRATIONS)
14 Videos
- BOARD'S QUESTION PAPER MARCH-2020 BOOK - KUMAR PRAKASHANCHAPTER - BOARD'S QUESTION PAPER MARCH-2020 EXERCISE - PART-B SECTION -C
4 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - KUMAR PRAKASHANCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section-D (MCQs asked in GUJCET/Board Exam)
1 Videos
Similar Questions
The current through a wire varies with time as I=I0+αt, where I0=10 A and α=4As−1 . The charge that flows across a cross-section of the wire in first 10 seconds is .....
View SolutionOne copper wire having resistivity 1.7 ×10−8Ω, density 8.9×103kgm−3, atomic weight 63.5 g mol−1 , length 0.1 m and cross-sectional area 10−6m2carries 1 A electric current. Find (i) potential difference across the wire (ii) drift velocity of free electron. (Avogadro number = 6.02×1023 mol−1 and valency of copper - 1
View Solution(a) Esttimate the average drift speed of conduction electrons in a copper wite of cross-secttonal area 1.0×10−7m2 carrying a current of 1.5A. Assume the each copper atom contrbutes roughly one conduction electron. The density of copper is 9.0×103kg/m3, and its atomic mass is 63.5u. (b) Compare the drift speed obyained above with, (1) thermal speeds of copper atoms at ordinary temperaturtes. (ii) speed of propagation of electric field along the conductor which causes the drift motion.
View SolutionDerive an expression for current I passing through an AC circuit containing only inductor L. Draw a Phasor diagram and graph of v and I versus ωt. Explain instantaneous power and the average power.
View SolutionMass of photon in motion is ………
View SolutionDetermine current in each branch of the network shown in figure

View Solution
Determine the current in each branch of the network shown in fig.
View SolutionDetermine the current in each branch of the network shown in Fig. 3.24

View SolutionDetermine the current in each branch of the network shown in fig.
View SolutionDetermine the current in each branch of the network shown in figure.
View SolutionDetermine the current in each branch of the network shown in
View SolutionDetermine the current in each branch of the network shown in Fig.
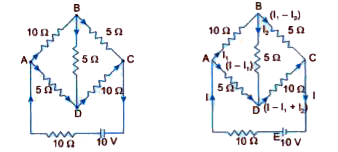
View SolutionDetermine the current in each branch of the network shown in fig.
View SolutionDetermine the current in each branch of the given network.

View SolutionDetermine the current in each branch of the network shown in figure.
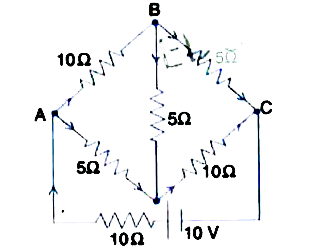
View Solution
