In the above problem time interval of which m strikes the pulley is √xMml(m+2m)F then 'x' is
The correct Answer is:2
Topper's Solved these Questions
- NEWTONS LAWS OF MOTION BOOK - AAKASH SERIESCHAPTER - NEWTONS LAWS OF MOTION EXERCISE - PRACTICE SHEET (EXERCISE - I) (LEVEL - I) (Straight Objective Type Questions)
14 Videos
- NEWTONS LAWS OF MOTION BOOK - AAKASH SERIESCHAPTER - NEWTONS LAWS OF MOTION EXERCISE - PRACTICE SHEET (EXERCISE - I) (LEVEL - II) (Straight Objective Type Questions)
5 Videos
- NEWTONS LAWS OF MOTION BOOK - AAKASH SERIESCHAPTER - NEWTONS LAWS OF MOTION EXERCISE - LECTURE SHEET (EXERCISE - VI) (Linked Comprehension Type Questions)
3 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Questions for Descriptive Answers
7 Videos
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
12 Videos
Similar Questions
In the figure shown, the strings and pulleys are massless. The blocks are in equilibrium. If the force by the clamp on the pulley is √83 mg then Mm is equal to
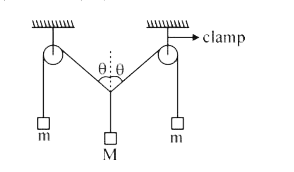
View SolutionIn the figure shown, the strings and pulleys are massless. The blocks are in equilibrium. If the force by the clamp on the pulley is √83 mg then Mm is equal to

View Solution
Knowledge Check
Area of square plot is 6561 m2 find the length of a diagonal of the square plot . The following are the steps involved in solving the above problem Arrange them in sequential order
(A) Area of the square plot =√2×x=81√2m
(B) Length of the diagonal =√2×x=81√2m
(C )Let the side of the square plot be x cm
(D) ∴ side of the square plot x=√6561=81mADCBABBCADCCADBDABDCThree blocks of masses m1,m2 and M are arranged as shown in figure. All the surfaces are fricationless and string is inextensible. Pulleys are light. A constant force F is applied on block of mass m1. Pulleys and string are light. Part of the string connecting both pulleys is vertical and part of the strings connecting pulleys with masses m1 and m2 are horizontal.
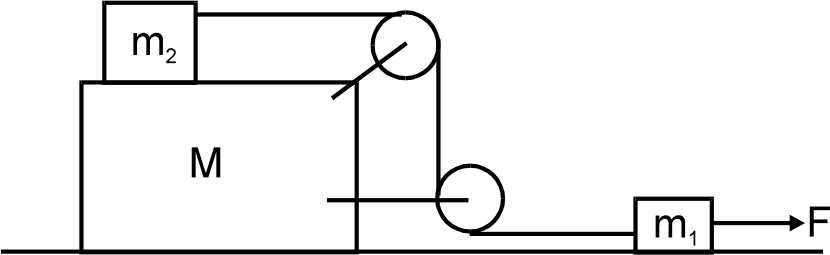
(P)Accleration of mass m1(1)Fm1(Q)Acceleration of massm2(2)Fm1+m2(R)Acceleration of mass M(3)zero(S)Tension in the string(4)m2Fm1+m2APQRS(A)2234BPQRS(B)2134CPQRS(C)2241DPQRS(D)2131If m is the minimum value of k for which the function f(x)=x√kx−x2 is increasing in the interval [0,3] and M is the maximum value of f in the inverval [0,3] when k=m, then the ordered pair (m,M) is equal to
A(4,3√2)B(4,3√3)C(3,3√3)D(5,3√6)
The least integral value of m, m ∈R for which the range of function f(x)=x+mx2+1 contains the interval [0,1] is :
View SolutionThe least integral value of m, m ∈R for which the range of function f(x)=x+mx2+1 contains the interval [0,1] is :
View SolutionIn the previous problem, particle strikes and sticks to rod. Repeat the problem (given m<<M).
View SolutionThree blocks of masses m1,m2 and M are arranged as shown in figure. All the surfaces are fricationless and string is inextensible. Pulleys are light. A constant force F is applied on block of mass m1. Pulleys and string are light. Part of the string connecting both pulleys is vertical and part of the strings connecting pulleys with masses m1 and m2 are horizontal.

(P)Accleration of mass m1(1)Fm1(Q)Acceleration of massm2(2)Fm1+m2(R)Acceleration of mass M(3)zero(S)Tension in the string(4)m2Fm1+m2
View SolutionAll the values of parameter m for which the functions f(x)=x33+(m−1)x2+(m+5)x+7 is increasing for all x>0 lie in the interval is equal to
View Solution
