Two circles of equal radii cut each other at P and Q, so that the centre of one lies on the other. A straight line through P cuts the circle again at A and B. Prove that ΔQAB is equilateral triangle.
Video Solution
Text Solution
QC2=r2−(r2)2
=34r2
QC=√32r
∠QOP=2⋅∠QOC
=1200
∠QRP=1202=600
∠QRPand∠QBP are inscribed on the arc PQ,
θ=600
∠QOP=∠QAP=1200
they are inscribed in the same are QSR
∠QAB=1800=∠QAP=1800=1200=600
All the angles are 600
Therefore, QAB is equilateral triangle.
|
Similar Questions
Knowledge Check
Two circles of unit radii, are so drawn that the centre of each lies on the circuference of the other. The area of the region , common to both the circles, is :
A(4π−3√3)12B(4π−6√3)12C(4π−3√3)6D(4π−6√3)6Two circles with radii 5 cm and 8 cm touch each other externally at a point A. If a straight line through the point A cuts the circles at points P and Q respectively, then AP : AQ is
A8:5B5:8C3:4D4:5Each of the circles of equal radii with centres A and B pass through the centre of one another circle they cut at C and D then ∠DBCis equal to
A60∘B100∘C120∘D140∘
Two equal circles intersect in P and Q . A straight line through P meets the circles in A and B . Prove that QA=QB.
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View SolutionABCD is a parallelogram, a line through A cuts DC at point P and BC produced at Q.
Prove that triangle BCP is equal in area to triangle DPQ.
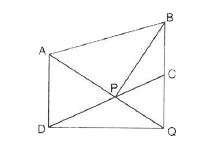
View SolutionABCD is a parallelogram, a line through A cuts DC at point P and BC produced at Q.
Prove that triangle BCP is equal in area to triangle DPQ.

View SolutionTwo circles of unit radii, are so drawn that the centre of each lies on the circuference of the other. The area of the region , common to both the circles, is :
View Solution
