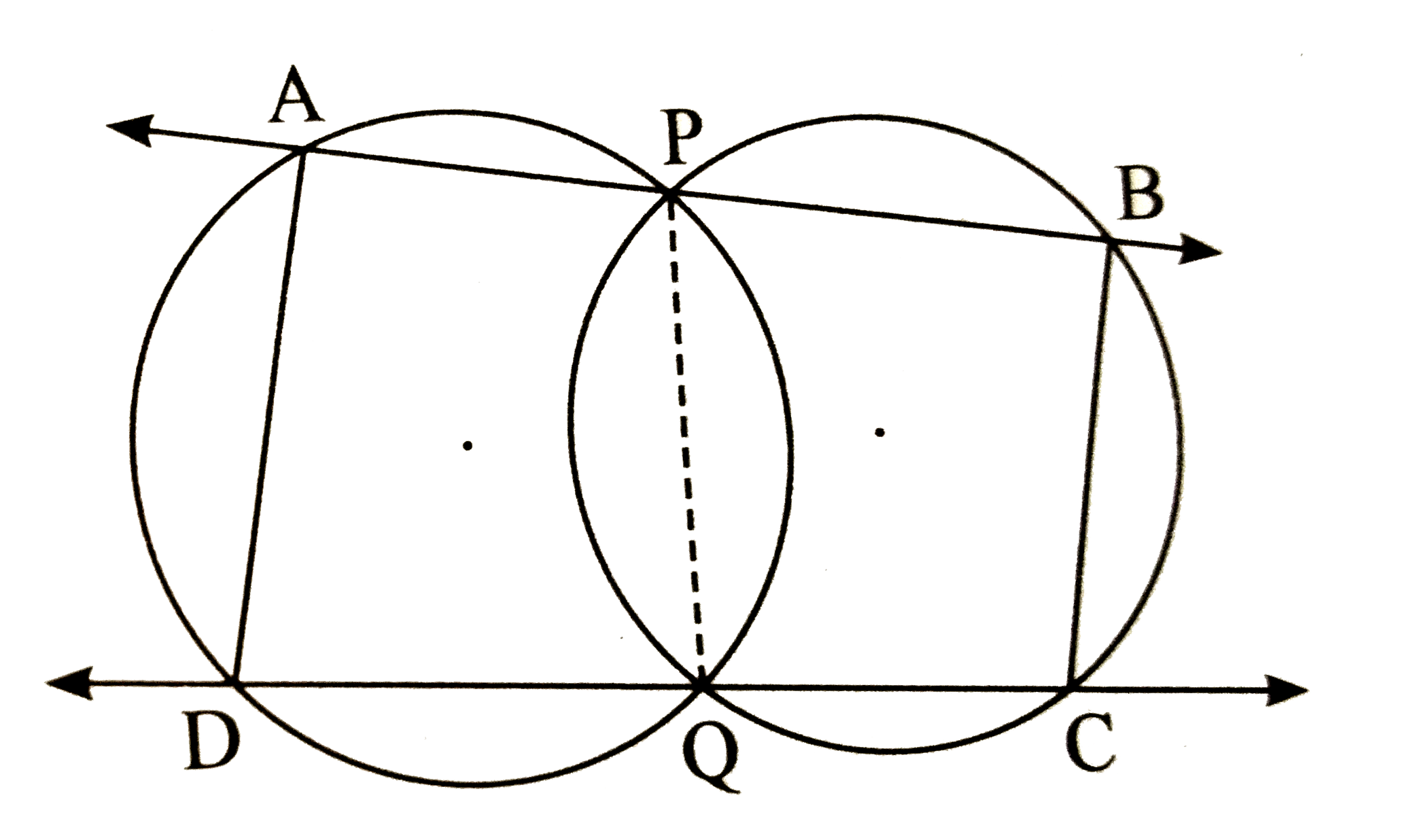
Two circles intersect each other at the points P and Q. Two straight lines through P and Q intersect on circle at the points A and C and the other circle at B and D . Prove that AC||BD.Solution in Bengali
we know that two opposite angles of a cyclic quadrilateral are supplementary.
for the quadrilateral ACQP,
and for the quadrilateral BPQD
…….(2)
Now adding (1) and(2) , we get
or,
or ,
But the common transversal of the straight lines AC and BD is AB and two adjacent angles on the same side of AB are , the sum of which is
AC||BD[ the sum of two adjacent angles on the same side of the common transversal of two straight lines ]
Hence AC||BD .

Topper's Solved these Questions
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - EXERCISE-3(Very short - answer type questions)(MCQ)
4 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Short -answer type question (S. A.)
2 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - EXAMPLE (Short - answer type questions)
5 Videos
- THEOREMS RELATED TO CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CIRCLE EXERCISE - EXERCISE - 1 (Long - answer type question )
9 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (Long Answer Type Questions)
14 Videos
Similar Questions
If the length of diagonal of a square is √72cm, then calculate the area of the square.
View SolutionIf the length of diagonal of a square is 12√2m, then calculate the area of the square.
View SolutionIn the adjoining figure , if ∠BAD=60∘.∠ABC=80∘ , then find the values of ∠DPCand∠BQC .
View SolutionProve that diameter is the greatest chord of a circle.
View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View Solutionदो समान वृत्त एक-दूसरे को बिन्दुओं A और B पर काटते हैं | A से होकर जाने वाली एक वृत्तों को P और Q बिन्दुओं पर मिलती है | सिद्ध कीजिए कि BP = BQ.
View SolutionTwo circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that :∠ADC+∠BCD=180∘
View SolutionThe centre of two circle are P and Q they intersect at the points A and B. The straight line parallel to the line segment PQ through the point A intersects the two circles at the point C and D Prove that CD=2PQ
View SolutionAnkita drew two circles which intersect each other at the points P and Q. Through the point P two straight lines are draw so that they intersect one of the circle at the points. A and B and the ohte circle at the points C and D respectively. Prove that ∠AQC=∠BQD.
View SolutionTwo circles intersect each other at the points P and Q. A straight line passing through P intersects one circle at A the other circle at .A straight line passing through Q intersect the first circle at C and the second circle at D. Prove that AC∣∣BD.
View SolutionTwo circles intersect each other at the points G and H . A straight line is drawn through the point G which intersect two circles at the points P and Q and the straight line through the point H parallel to PQ intersects the two circles at the points R and S . Prove that PQ=RS .
View SolutionIn two circles , one circle passes through the centre O of the other circle and they intersect each other at the points A and B . A straight line passing through A intersect the circle passing through O at the point P and the circle with centre at O at the point R . BY joining P , B and R , B prove that PR= PB.
View SolutionTwo chords AC and BD of a circle intersect each other at the point O. If two tangents drawn at the points A and B intersect each other at the point P and two tangents drawn at the points C and D intersect at the point Q, prove that ∠P+∠Q=2∠BOC.[GP−X]
View SolutionTwo circles intersect each other at P externally. The straight QR touches the circle at two points Q and R. Prove that ∠QPR=1 right angle.
View Solution
