For an LCR circuit driven at frequency ω, the equation reads Ldidt+Ri+qC=υi=υmsinωt
(i) Multiply the equation by I and simplify where possible. (ii) Interpret each term physically.
(iii) Cast the equation in the form of a conservation of energy statement.
(iv) Intergrate the equation over one cycle to find that the phase difference between υ and i must be acute.
The correct Answer is:A
To solve the problem step by step, we will address each part of the question systematically.
1. LIdidt: This term represents the rate of change of energy stored in the inductor. It signifies how the current change affects the magnetic field and energy in the inductor.
2. RI2: This term represents the power loss due to resistance (Joule heating). It indicates how much energy is dissipated as heat in the resistor.
3. qIC: This term represents the rate of change of energy stored in the capacitor. It relates to how the charge on the capacitor affects the electric field and energy stored in it.
4. Iυmsin(ωt): This term represents the power supplied by the source. It shows how the input voltage drives the current in the circuit.
(iii) Cast the equation in the form of a conservation of energy statement.
Rearranging the equation gives:
LIdidt+RI2+qIC−Iυmsin(ωt)=0
This can be interpreted as a conservation of energy statement:
- The energy increase in the inductor (first term) plus the energy stored in the capacitor (third term) must equal the energy lost in the resistor (second term) and the energy supplied by the source (fourth term).
(iv) Integrate the equation over one cycle to find that the phase difference between υ and I must be acute.
Integrate the equation over one cycle T:
∫T0(LIdidt+RI2+qIC−Iυmsin(ωt))dt=0
This leads to:
∫T0LIdidtdt+∫T0RI2dt+∫T0qICdt=∫T0Iυmsin(ωt)dt
The left-hand side represents energy stored and dissipated, while the right-hand side represents energy supplied.
Since RI2 is always positive and the integral of Iυmsin(ωt) over one cycle is positive, it implies that the energy supplied is greater than the energy dissipated, which can only happen if the phase difference ϕ between υ and I is acute (i.e., 0<ϕ<90∘).
2. RI2: This term represents the power loss due to resistance (Joule heating). It indicates how much energy is dissipated as heat in the resistor.
LIdidt+RI2+qIC−Iυmsin(ωt)=0
- The energy increase in the inductor (first term) plus the energy stored in the capacitor (third term) must equal the energy lost in the resistor (second term) and the energy supplied by the source (fourth term).
∫T0(LIdidt+RI2+qIC−Iυmsin(ωt))dt=0
∫T0LIdidtdt+∫T0RI2dt+∫T0qICdt=∫T0Iυmsin(ωt)dt
Topper's Solved these Questions
Similar Questions
Two SHM are represented by equations x1=4sin(ωt+37°) and x2=5cos(ωt). The phase difference between them is
View SolutionThere is a 5Ω resistance in an AC, circuit. Inductance of 0.1H is connected with it in series. If equation of AC emf is 5sin50t then the phase difference between current and e.m.f. is
View SolutionTwo particle AandB execute simple harmonic motion according to the equation y1=3sinωt and y2=4sin[ωt+(π/2)]+3sinωt. Find the phase difference between them.
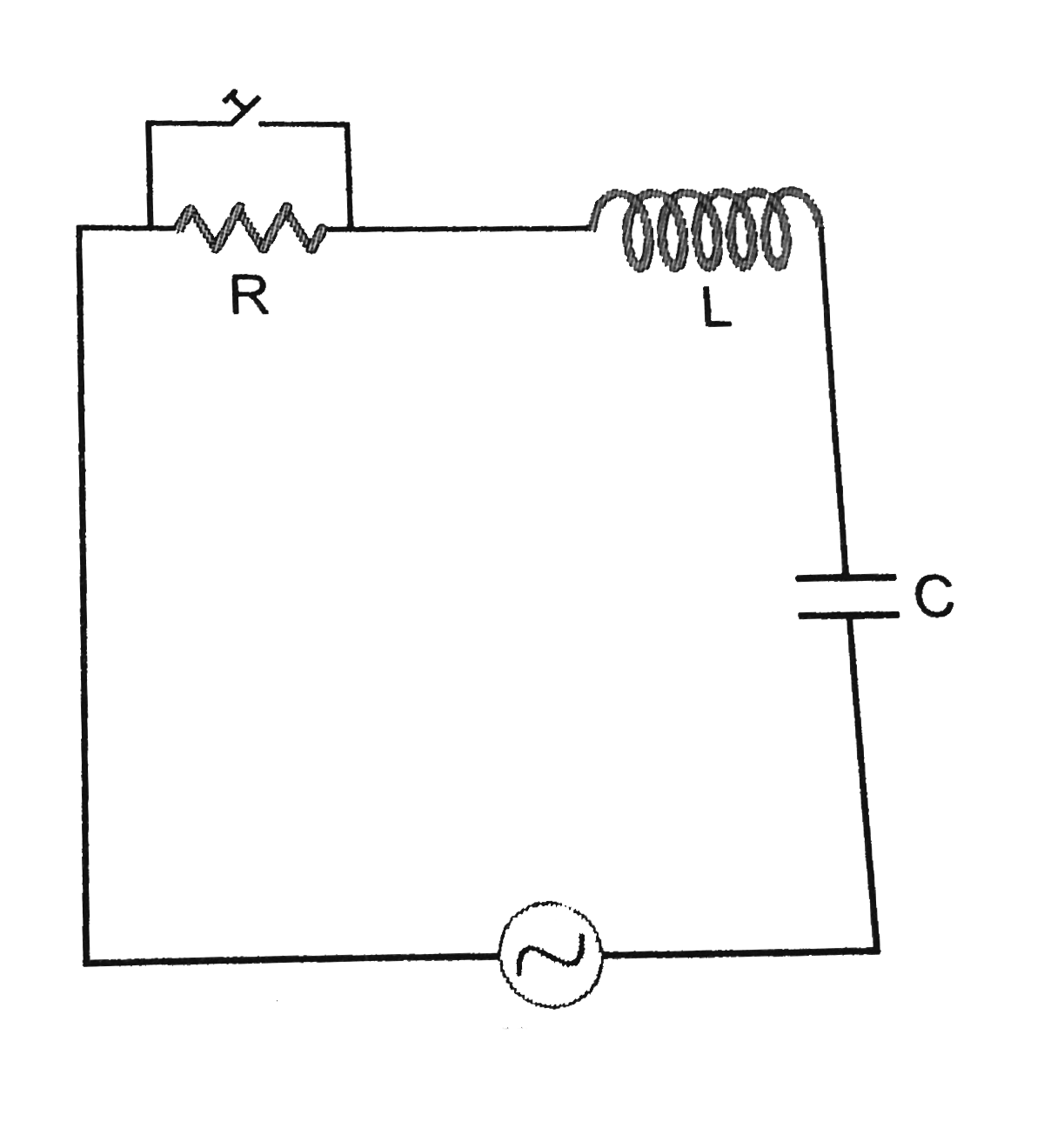
View SolutionIn the LCR circuit shown in Fig., the ac driving voltage is υ=υmsinωt.
(i) Write down the equation of motion for q (t).
(ii) At t=t0, the source stops and R is short circuited.
Now write down how much energy is stored in each of L and C.
(iii) Describe subsequent motion of charges.
View SolutionIf i1=3sinωtand(i2)=4cosωt, then (i3) is

View SolutionThe equation of an alternating voltage is E=220sin(ωt+π/6) and the equation of the current in the circuit is I=10sin(ωt−π/6). Then the impedance of the circuit is
View Solutionx1=3sinωt , x2=4cosωt. Find (i) amplitude of resultant SHM, (ii) equation of the resultant SHM.
View SolutionWhat is kinetic gas equation ? What is the significance of each term in the equation ? Deduce (i) Boyle's law (ii) Charles's law from the kinetic gas equation.
View SolutionGiven magnetic field equation isB=3×10−8sin(ωt+kx+ϕ)ˆjthen appropriate equation for electric field (E) will be :
View SolutionFind the equation of a line whose
(i) slope =-3 and y-intercept =5 (ii) m=8 and c=-6
View Solution
