In the adjoining figure
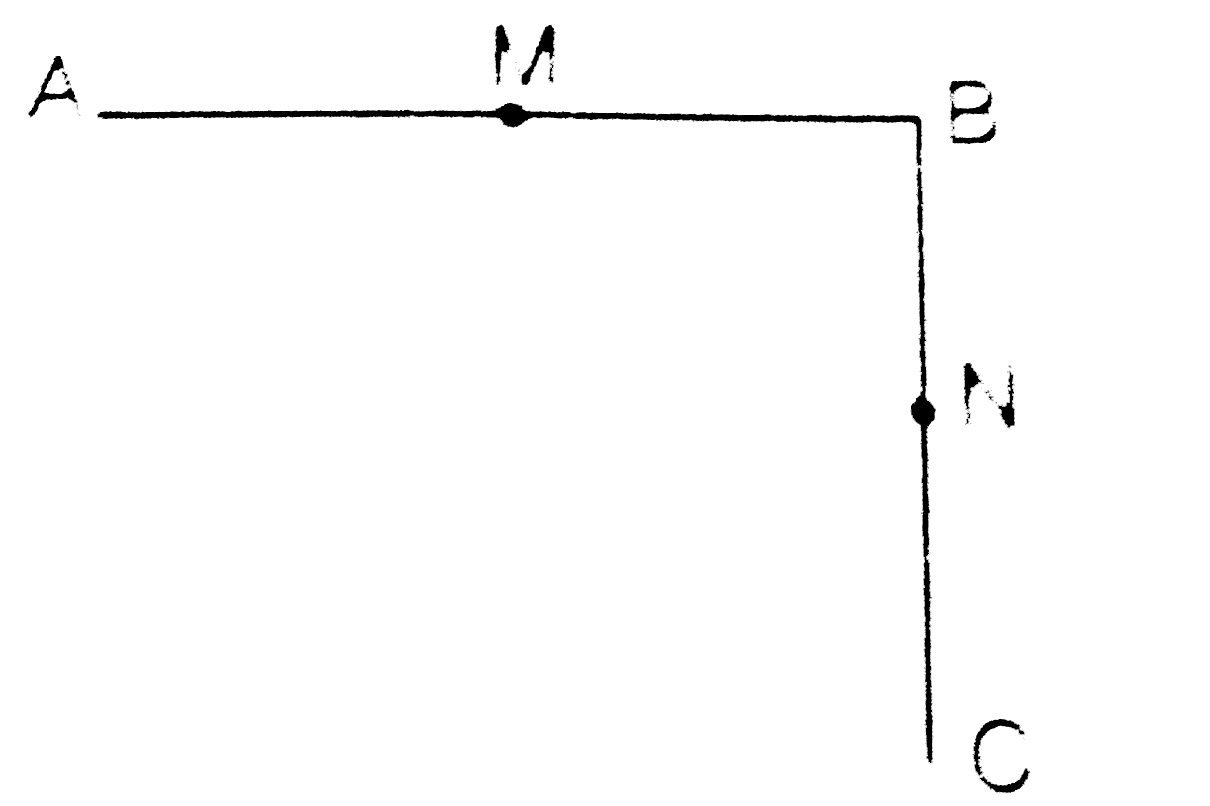
(i) AB=BC, M is the mid -point of AB and N is the mid- point of BC. Show that AM=NC.
(ii) BM=BN,M is the mid- point of AB and N is the mid - point of BC. Show that AB=BC.
Given, AB=BC …(i)
M is the mid - point of AB.
AM=MB=12AB …(ii)
and N is the mid - point of BC.
BN=NC=12BC …(iii)
According to Euclid's axiom , things which are halves of the same things are equal to one another . From Eq. (i) , AB=BC
On multiplying both sides by 12 , we get
12AB=12BC
⇒AM=NC [using Eqs. (ii) and (iii)]
(ii) Given, BM=BN ...(i)
M is the mid -point of AB.
∴AM=BM=12AB
⇒2AM=2BM=AB ...(ii)
and N is the mid - point of BC.
∴BN=NC=12BC
⇒2BN=2NC=BC ...(iii)
According to Euclid's which are double of the same thing are equal to one another.
On multiplying both sides of Eq.(i) by 2, we get
2BM=2BN
⇒AB=BC [using Eqs. (ii) and (iii)]
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INTRODUCTION TO EUCLID GEOMETRYEXERCISE - Exercise 5.4 Long Answer Type Questions5videos
INTRODUCTION TO EUCLID GEOMETRY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INTRODUCTION TO EUCLID GEOMETRYEXERCISE - Exercise 5.2 Very Short Answer Type Questions9videos
INTRODUCTION TO EUCLID GEOMETRY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - HERON'S FORMULAEXERCISE - Long Answer Type Questions8videos
HERON'S FORMULA
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR EQUATION IN TWO VARIABLESEXERCISE - Exercise 4.81videos
LINEAR EQUATION IN TWO VARIABLES
Similar Questions
ABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
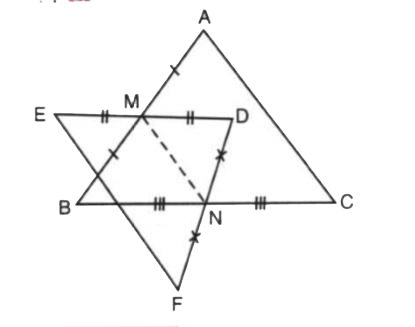
∠DXA=∠AYBView SolutionIn the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF. Show that : EF = AC.
 View Solution
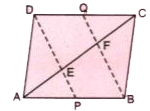
View SolutionThe adjoining figure shows a parallelogram ABCD in which P is mid-point of AB and Q is mid-point of CD. Prove that AE=EF=FC.
 View Solution
View SolutionIn the figure, given below, 2AD=AB,P is the mid-point of AB, Q is the mid-point of DR and PR∣∣BS. Prove that :
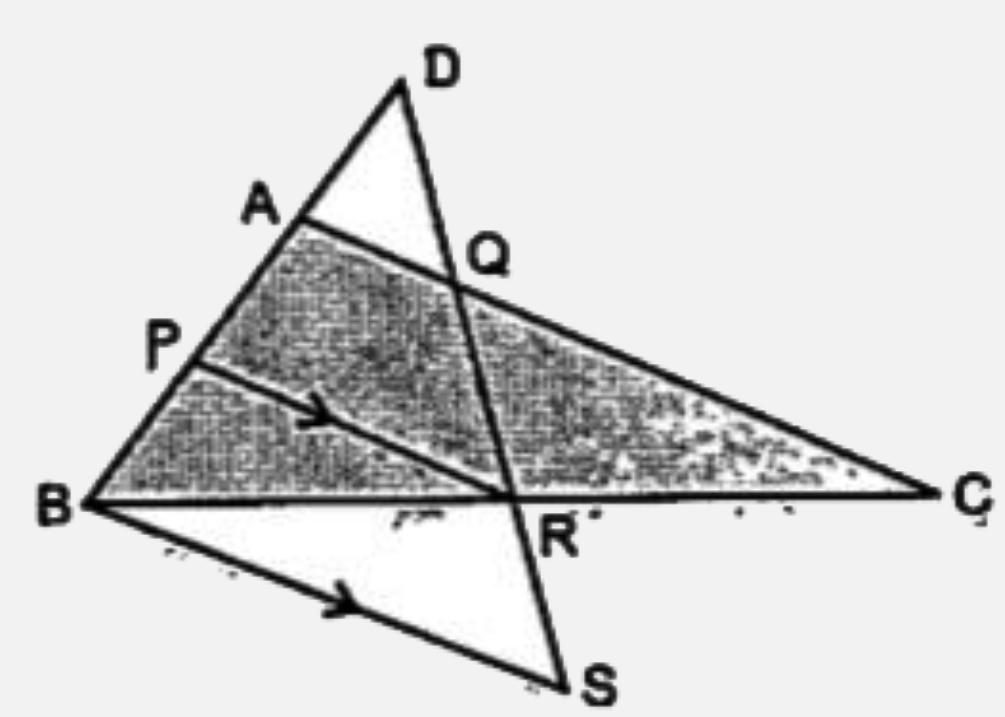
DS=3RSView SolutionIn the figure, given below, 2AD=AB,P is the mid-point of AB, Q is the mid-point of DR and PR∣∣BS. Prove that :

AQ∣∣BSView SolutionABCD is a square, X is the mid-point of AB and Y the mid-point of BC. Prove that
DX is perpendicular to AY.View SolutionIn the adjoining figure , we have X and Y are the mid - point of AC and BC and AX = CY . Show that AC =BC.
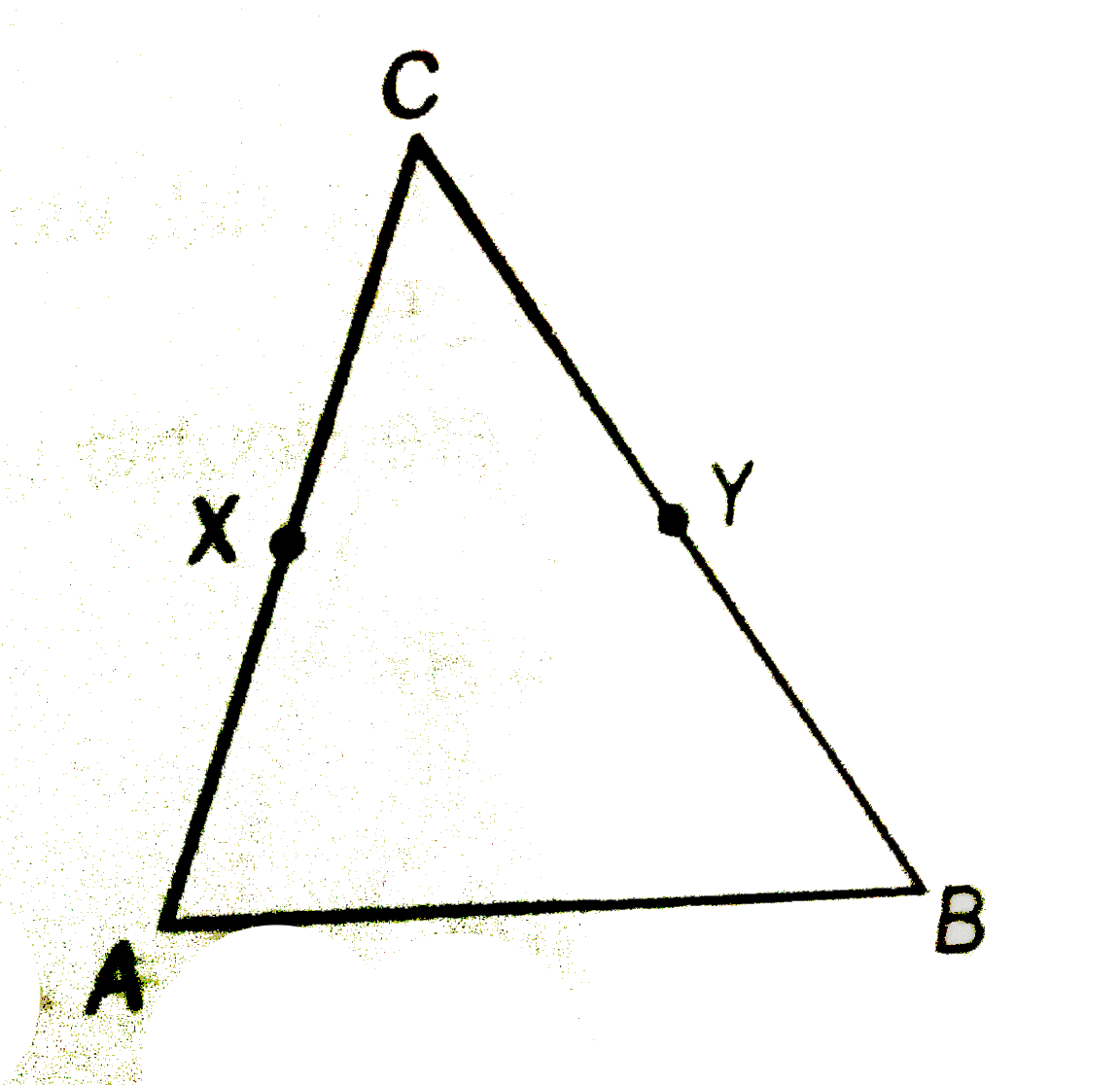 View Solution
View SolutionIn parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
View SolutionIn the figure, given below, 2AD = AB, P is mid-point of AB, Q is mid-point of DR and PR // BS. Prove that:
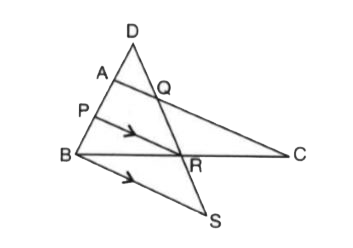
AQ//BSView SolutionIn trapezium ABCD, AB//DC. M is mid point of AD and N is mid-point of BC.
If AB = 8 cm and DC = 11 cm , find MN.View Solution

