A , given that QR = 3cm, and QP - PR = 2cm.
Given, in , QR = 3cm
and = 2cm
To construct , use the following steps.
(i) Draw the base QR of length 3cm.
(ii) Make an angle XQR = at point Q of base QR.
(iii) Cut the line segment QS = QP - PR = 2cm from the ray QX.
(iv) Join SR and draw the perpendicular bisector of SR say AB.
(v) Let bisector AB intersect QX at P. Join PR Thus, is the required triangle.
Justification
Base QR and are drawn as given. Since, the point P lies on the perpendicular bisector of SR.
PS = PR
Now, QS = PQ-PS
= PQ - PR
Thus , our construction is justified.

Topper's Solved these Questions
- CONSTRUCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Short Answer Type Questions
8 Videos
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.4
14 Videos
- COORDINATE GEOMETRYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 3.4 Long Answer Type Questions
5 Videos
Similar Questions
Construct a triangle PQR, in which QR=4.5cm, ∠Q=44∘ and PQ−PR=2cm.
View Solution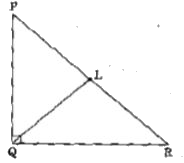
In the figure given above, ∠PQR=90∘ and QL is a median, PQ=5cmandQR=12cm, Then QL is equal to:
View SolutionIn ΔPQR,∠R=∠PandQR=4cmandPR=5cm . Then find the value of length of PQ×QR×PR.
View SolutionIn ΔPQR , right - angled at Q , PR +QR = 25 cm and PQ = 5cm . Determine the values of sin P , cos P and tan P.
View SolutionIn ΔPQR , right - angled at Q , PR +QR = 25 cm and PQ = 5cm . Determine the values of sin P , cos P and tan P.
View SolutionIn ΔPQR , with ∠Q at right angle, given that PR+QR=25 cm and PQ=5 cm . Find the value of :
(i) sinP,cosP and tanP .
(ii) secR−cotP .

View SolutionIn ΔPQR right angled at Q , PQ = 3 cm and PR = 6 cm .
Determine side QR.
View SolutionConstruct a parallelogram PQRS, when PQ=3.7cm,QR=2.3cm,andPR=4.8cm.

View SolutionPQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

area of ΔPQRarea of ΔSPR
View SolutionPQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR=∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.

Prove ΔPQR~ΔSPR.
View Solution
