The zeroes of the quadratic polynomial $x^{2} + k x + k$ where $k \neq 0$ , are : (1)cannot both be positive (2)cannot both be negative (3)are always unequal (4)are always equal

A

cannot both be positive

B

cannot both be negative

C

are always unequal

D

are always equal

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Let $p (x) = x^{2} + k x + k, k \neq 0$
On comparing $p (x)$ with $a x^{2} + b x + c$ , we get
$a = 1, b = k$ and $c = k$
Now, $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ [by quadratic formula]
$= \frac{- k \pm \sqrt{k^{2} - 4 k}}{2 \times 1}$
$= \frac{- k \pm \sqrt{k (k - 4)}}{2}, k \neq 0$
Here, we see that
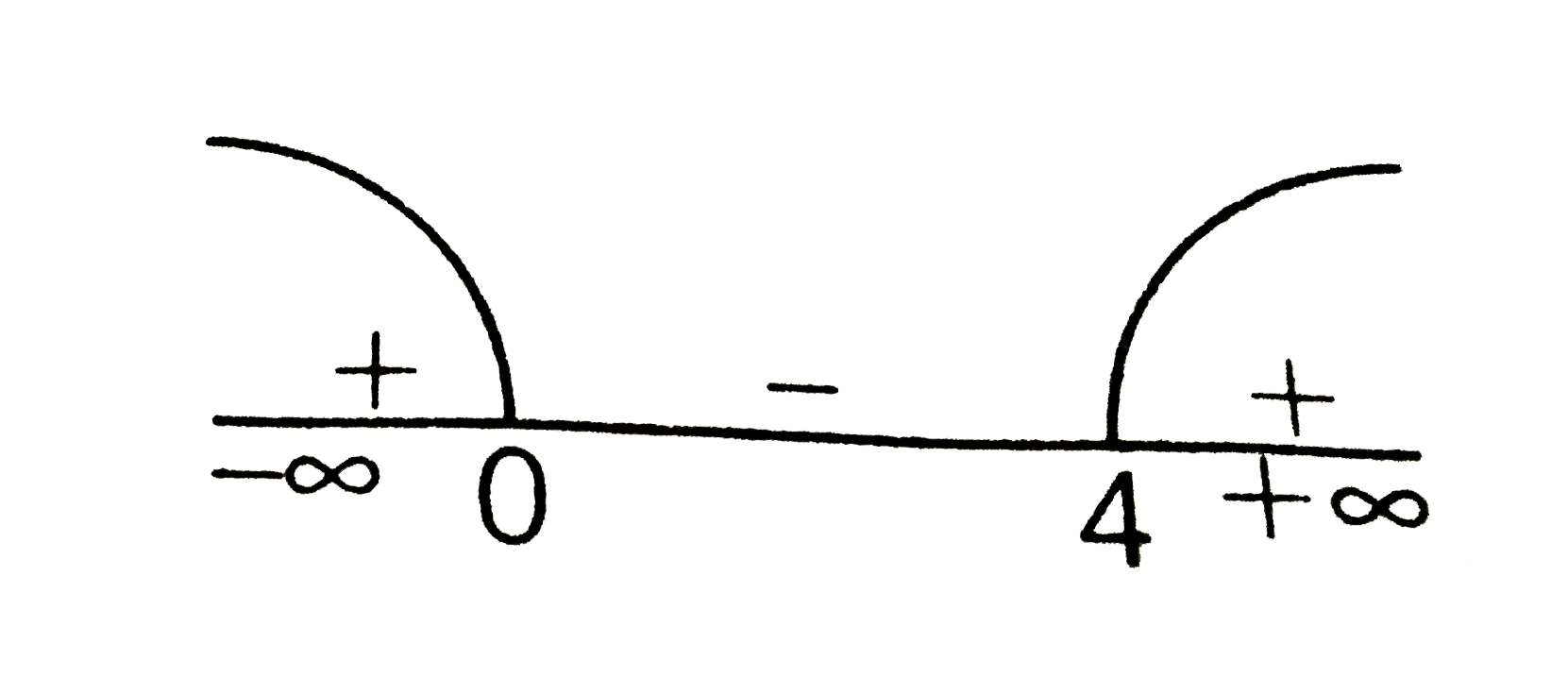
$k (k - 4) > 0$
$\Rightarrow k \in (- \infty, 0) \cup (4, \infty)$
Now, we know that
In quadratic polynomial $a x^{2} + b x + c$
If $a > 0, b > 0, c > 0$ or $a < 0, b < 0, c < 0$ ,
then the polynomial has always all negative zeroes. and is $a > 0, c < 0$ or $a < 0, c > 0$ , then the polynomial has always zeroes of opposite sign.
Case I if $k \in (- \infty, 0)$ i.e., $k < 0$
$\Rightarrow a = 1 > 0, b, c = k < 0$
So, the zeroes are of opposite sign.
Case II If $k \in (4, \infty) i . e ., k \geq 4$
$\Rightarrow a = 1 > 0, b \geq 4$
So, both zeroes are negative
Hence, in any case zeroes of the given quadratic polynomial cannot both be positive.

Updated on:21/07/2023

|

Class 10 MATHS POLYNOMIALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

If the roots of the quadratic equation $2 k x^{2} + (2 a + b) x - a b = 0$ are (-2, a), the value of k is:
A $- 1$
B $- 2$
C1
D2

NCERT EXEMPLAR ENGLISH-POLYNOMIALS -Long Answer Type Questions

Home
Ask Doubt
Profile