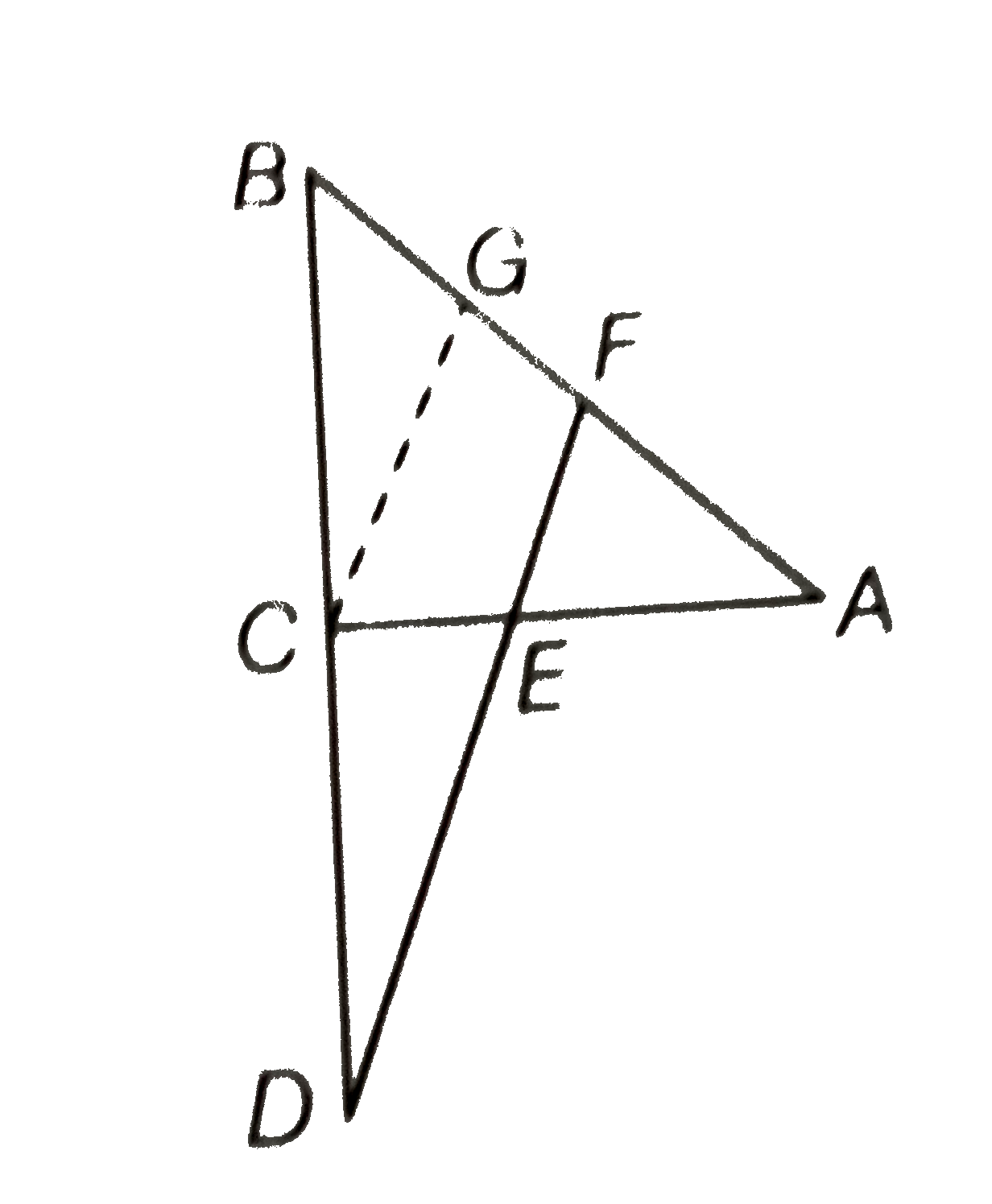
In figure, line segment DF intersects the side AC of a ΔABC at the point E such that E is the mid-point of CA and ∠AEF=∠AFE. Prove that BDCD=BFCE

Given ΔABC, E is the mid-point of CA and ∠AEF=∠AFE
To prove BDCD=BFCE
Construction Take a point G on AB such that CG||EF.
Proof Since, E is the mid point of CA.
∴CE=AE…(i)
In ΔACG,CG||EfandE is the mid point of CA....(ii)
So, CE=GF...(ii)
[by mid point theorem]
Now in ΔBCGandΔBDF,CG||EF
∴BCCD=BGGF [ by basic proportionality theorem]
⇒BCCD=BF−GFGF⇒BCCD−1
⇒BCCD+1=BFCE [from Eq. (ii)]
⇒BC+CDCD=BFCE⇒BDCD=BFCE Hence proved.
Topper's Solved these Questions
Similar Questions
In the given figure, D is a point on side BC of a ΔABC and E is a point such that CD = DE.
Prove that AB+AC>BE.
View SolutionIn Figure O is the mid-point of AB and CD. Prove that AOC≅ BOD (b) AC=BD (iii) AC∣∣BD
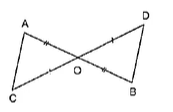
View SolutionIn Figure O is the mid-point of aB and CD. Prove tat AC=BD and AC||BD.

View SolutionIn figure l||m and M is the mid-point of the line segment AB. Prove that M is also the mid-point of line segment CD.

View SolutionIn the given figure, D and E are the points on the base BC of ΔABC such that BD=CE,AD=AE and ∠ADE=∠AED, prove that ΔADB≅ΔAEC.
View SolutionIn the given figure, D and E are the points on the base BC of ΔABC such that BD=CE,AD=AE and ∠ADE=∠AED, prove that ΔADB≅ΔAEC.

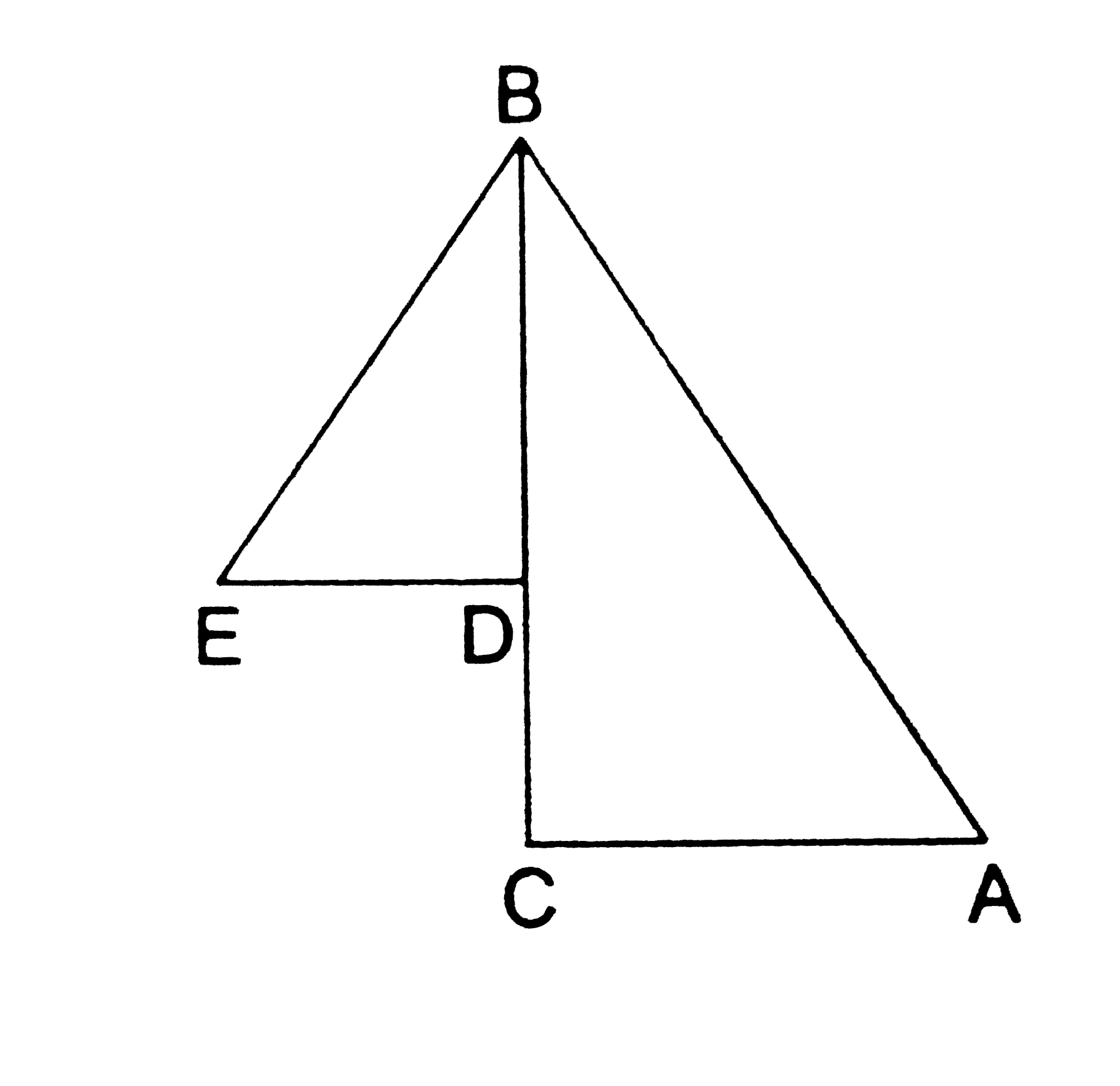
View SolutionIn the given figure D is mid-point of AB. DE//BC and DF //AC . Prove that : DE = BF

View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

View SolutionThe diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the side BC . Prove that DFxEF=FBxFA.
View Solution
