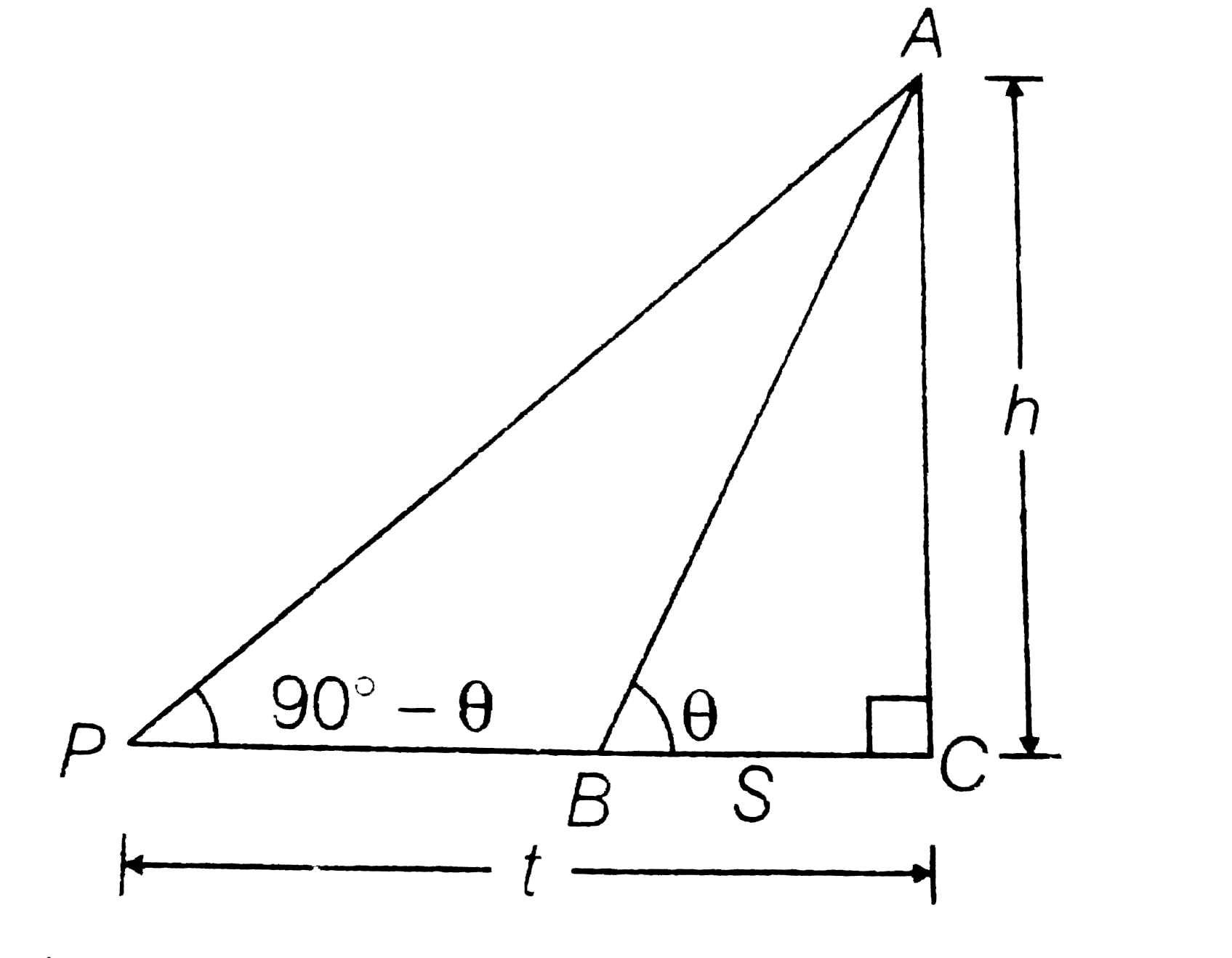
The angle of elevation of the top of a tower from two distinct points s and t from foot are complementary. Prove that the height of the tower is √st.
Let the height of the tower is h.
and ∠ABC=θ
Given that, BC=s, PC=t
and angle of elevation on both positions are complementary.
i.e., ∠APC=90∘−θ
[If two angles are complementary to each other, then the sum of both angles is equal to 90∘]
Now in ΔABC, tanθ=ACAB=hs ...................(i)
and in ΔAPC
tan(90∘−θ)=ACPC [∴tan(90∘−θ)=cotθ]
⇒cotθ=ht
⇒1tanθ=ht [∴cotθ=1tanθ]...............(ii)
On multyplying Eqs. (i) and (ii), we get
tanθ.1tanθ=hsht
⇒h2st=1
⇒h2=st
⇒h=√st
So, the required height of the tower is √st Hence Proved.
Topper's Solved these Questions
- INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONSEXERCISE - SHORT ANSWER TYPE QUESTIONS
15 Videos
- COORDINATE GEOMETRYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - COORDINATE GEOMETRYEXERCISE - Exercise 7.4 Long Answer Type Questions
6 Videos
- PAIR OF LINEAR EQUATIONS IN TWO VARIABLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PAIR OF LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Exercise 3.4 Long Answer Type Questions
13 Videos
Similar Questions
The angle of elevation of the top of a tower at a point on the ground 50m away from the foot of the tower is 450. Then the height of the tower (in metres) is 50√3 (b) 50 (c) 50√2 (d) 50√3
View SolutionThe angles of elevation of the top of a tower from two points at a distances a meter and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is √ab metres.
View SolutionThe angle of elevation of the top of a tower from a point 40 m away from its foot is 60∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30m away from the foot of the tower is 30∘ . Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30m away from the foot of the tower, is 30∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground is 60∘. which is 25 m away from the foot of the tower. Find the height of the tower
View SolutionThe angles of elevation of the top of a tower at the top and the foot of a pole of height 10 m are 30∘and60∘ respectively. The height of the tower is
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6m.
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
View Solution
