The tangent to the circumcircle of an isosceles ΔABC at A, in which AB= AC, is parallel to BC.
To solve the problem, we need to show that the tangent to the circumcircle of isosceles triangle ABC at point A is parallel to side BC. Here’s a step-by-step solution:
Step 1: Understand the Given Information
We have an isosceles triangle ABC where AB = AC. The tangent at point A on the circumcircle of triangle ABC is denoted as line XY. We need to prove that line XY is parallel to line BC.
Hint: Identify the properties of isosceles triangles and the concept of tangents to circles.
Step 2: Draw the Diagram
Draw triangle ABC such that AB = AC. Mark the circumcircle of triangle ABC, and draw the tangent line XY at point A. Label the points as follows:
- A (the vertex where the two equal sides meet)
- B (one endpoint of the base)
- C (the other endpoint of the base)
- X and Y (points on the tangent line)
Hint: Visualizing the problem can help you understand the relationships between the angles and lines.
Step 3: Identify Equal Angles
Since triangle ABC is isosceles, the angles opposite the equal sides are equal:
- Let angle ABC = angle ACB. We can denote these angles as θ.
Hint: Use the properties of isosceles triangles to establish relationships between the angles.
Step 4: Apply the Alternate Segment Theorem
According to the Alternate Segment Theorem, the angle formed by the tangent and a chord through the point of contact is equal to the angle in the alternate segment. Here, we have:
- Angle XAB (the angle between the tangent XY and chord AB) is equal to angle ACB (the angle in the alternate segment).
Hint: Remember the Alternate Segment Theorem is crucial for relating the angles formed by tangents and chords.
Step 5: Establish Relationships Between Angles
From the previous steps, we have:
- Angle XAB = angle ACB = θ.
Now, since angle ABC = θ (from Step 3), we can conclude:
- Angle XAB = angle ABC.
Hint: This equality of angles is key to proving the lines are parallel.
Step 6: Use the Transversal Property
Since line AB acts as a transversal between lines XY and BC, and we have established that:
- Angle XAB = angle ABC,
we can conclude that lines XY and BC are parallel by the Alternate Interior Angles Theorem.
Hint: Recall that if a transversal intersects two lines and the alternate interior angles are equal, then the lines are parallel.
Conclusion
Thus, we have shown that the tangent XY at point A is parallel to side BC of triangle ABC.
---
We have an isosceles triangle ABC where AB = AC. The tangent at point A on the circumcircle of triangle ABC is denoted as line XY. We need to prove that line XY is parallel to line BC.
Draw triangle ABC such that AB = AC. Mark the circumcircle of triangle ABC, and draw the tangent line XY at point A. Label the points as follows:
- A (the vertex where the two equal sides meet)
- B (one endpoint of the base)
- C (the other endpoint of the base)
- X and Y (points on the tangent line)
Since triangle ABC is isosceles, the angles opposite the equal sides are equal:
- Let angle ABC = angle ACB. We can denote these angles as θ.
According to the Alternate Segment Theorem, the angle formed by the tangent and a chord through the point of contact is equal to the angle in the alternate segment. Here, we have:
- Angle XAB (the angle between the tangent XY and chord AB) is equal to angle ACB (the angle in the alternate segment).
From the previous steps, we have:
- Angle XAB = angle ACB = θ.
- Angle XAB = angle ABC.
Since line AB acts as a transversal between lines XY and BC, and we have established that:
- Angle XAB = angle ABC,
we can conclude that lines XY and BC are parallel by the Alternate Interior Angles Theorem.
Thus, we have shown that the tangent XY at point A is parallel to side BC of triangle ABC.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.3 SHORT ANSWER TYPE QUESTIONS10videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.4 LONG ANSWER TYPE QUESTIONS14videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.4 LONG ANSWER TYPE QUESTIONS14videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Long Answer Type Questions10videos
ARITHMETIC PROGRESSIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions7videos
CONSTRUCTIONS
Similar Questions
If the radius of the circumcircle of the isosceles triangle ABC is equal to AB(=AC), then the angle A is equal to-
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC. Side CP is parallel to AB and AP is the bisector of exterior angle CAD of Δ ABC. Prove that ∠PAC=∠BCAand□ABCP is a parallelogram.
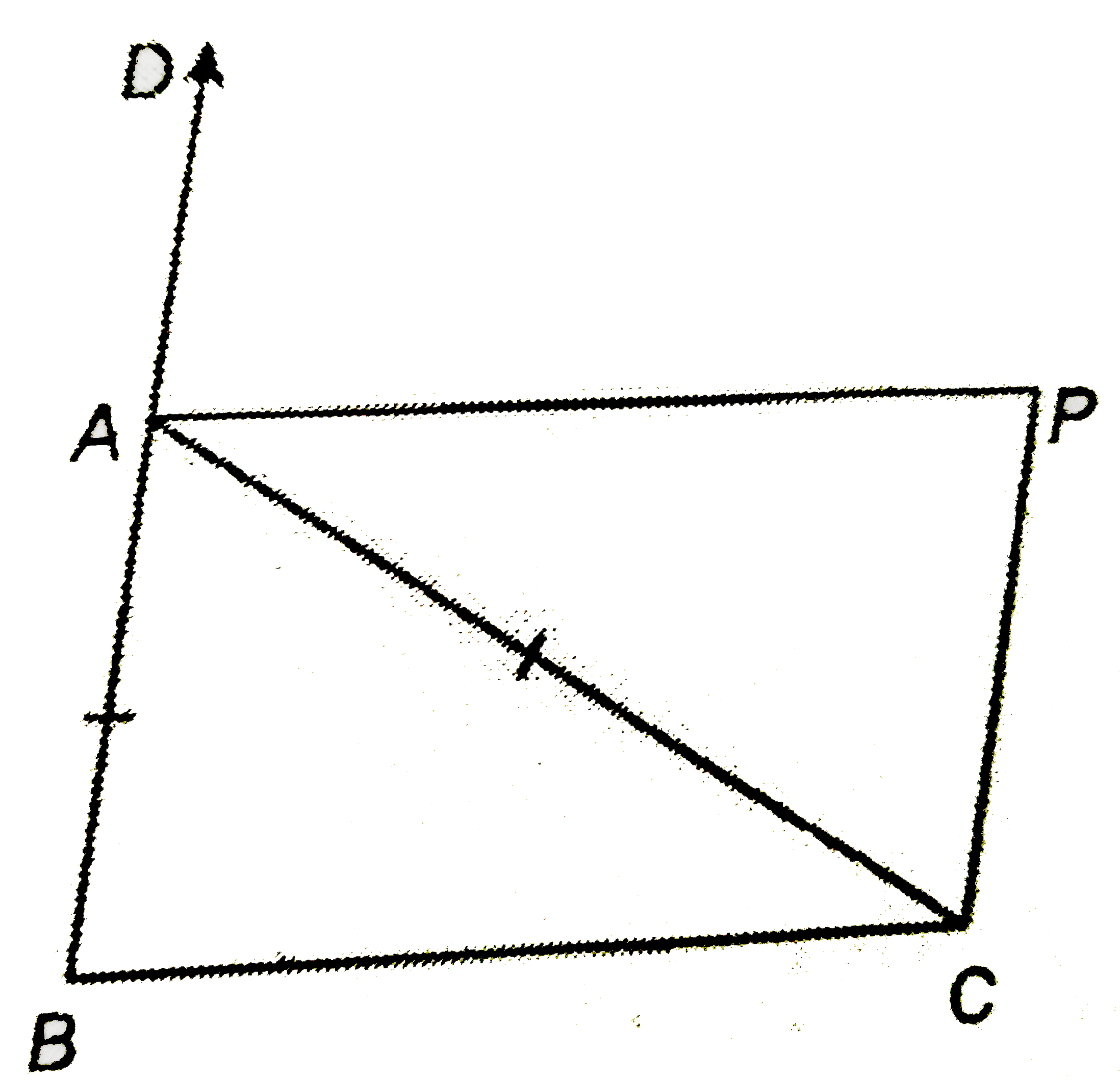 View Solution
View SolutionConstruct an isosceles ΔABC in which base BC = 5 cm and ∠B=60∘.
View SolutionExtremities of a diagonal of a rectangle are (0, 0) and (4, 3). The equations of the tangents to the circumcircle of the rectangle which are parallel to the diagonal, are
View SolutionThe extremities of a diagonal of a rectangle are (0,0) and (4,3). The equation of tangents to the circumcircle of the rectangle which are parallel to the diagonal are
View SolutionTangent at P to the circumcircle of triangle PQR is drawn. If this tangent is parallel to side QR show that ΔPQR is isosceles.
View SolutionConstruct an isosceles ΔABC in which base BC = 5 cm and side AB = 4 cm.
View SolutionAD is an altitude of an isosceles ΔABC in which AB = AC.
Show that (i) AD bisects BC,
(ii) AD bisects ∠A.
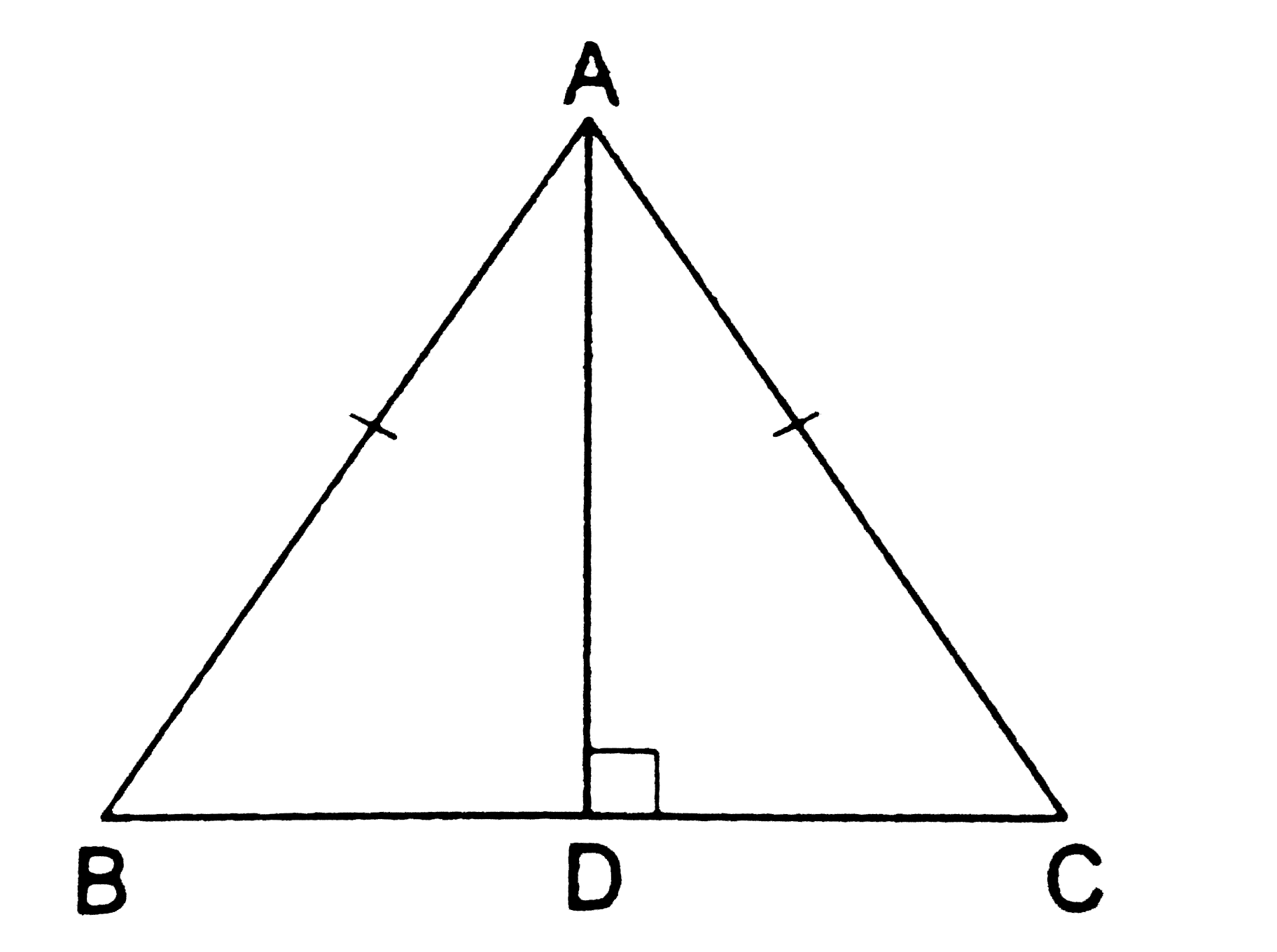 View Solution
View SolutionD, E and F are the mid-points of the sides AB, BC and CA of an isosceles triangle ABC in which AB = BC. Prove that ΔDEF is also isosceles.
View SolutionLet G be the centroid of triangle ABC and the circumcircle of triangle AGC touches the side AB at A
If BC=6,AC=8, then the length of side AB is equal toView Solution

