If a hexagon ABCDEF circumscribe a circle, prove that
To prove that for a hexagon ABCDEF that circumscribes a circle, the equation AB+CD+EF=BC+DE+FA holds, we can follow these steps:
1. Understanding the Hexagon and Circle:
- We have a hexagon ABCDEF that circumscribes a circle. This means that the circle touches each side of the hexagon at exactly one point.
2. Label the Points of Tangency:
- Let the points where the circle touches the sides of the hexagon be labeled as follows:
- The circle touches side AB at point R,
- Side BC at point S,
- Side CD at point T,
- Side DE at point U,
- Side EF at point V,
- Side FA at point W.
3. Using the Tangent Property:
- Recall that the lengths of tangents drawn from an external point to a circle are equal. Therefore, we can write the following equalities based on the points of tangency:
- From point A: AR=AW (Equation 1)
- From point B: BR=BS (Equation 2)
- From point C: CT=CS (Equation 3)
- From point D: DT=DU (Equation 4)
- From point E: EU=EV (Equation 5)
- From point F: FW=FV (Equation 6)
4. Adding the Tangent Lengths:
- Now, we add all the equations:
AR+BR+CT+DT+EU+FW=AW+BS+CS+DU+EV+FV
5. Rearranging the Sums:
- We can rearrange the left side to group the segments that correspond to the sides of the hexagon:
- (AR+BR)+(CT+DT)+(EU+FW)=AB+CD+EF
- And for the right side:
- (BS+CS)+(DU+EU)+(AW+FW)=BC+DE+FA
6. Final Equation:
- Thus, we have:
AB+CD+EF=BC+DE+FA
- This completes the proof.
- We have a hexagon ABCDEF that circumscribes a circle. This means that the circle touches each side of the hexagon at exactly one point.
- Let the points where the circle touches the sides of the hexagon be labeled as follows:
- The circle touches side AB at point R,
- Side BC at point S,
- Side CD at point T,
- Side DE at point U,
- Side EF at point V,
- Side FA at point W.
- Recall that the lengths of tangents drawn from an external point to a circle are equal. Therefore, we can write the following equalities based on the points of tangency:
- From point A: AR=AW (Equation 1)
- From point B: BR=BS (Equation 2)
- From point C: CT=CS (Equation 3)
- From point D: DT=DU (Equation 4)
- From point E: EU=EV (Equation 5)
- From point F: FW=FV (Equation 6)
- Now, we add all the equations:
AR+BR+CT+DT+EU+FW=AW+BS+CS+DU+EV+FV
- We can rearrange the left side to group the segments that correspond to the sides of the hexagon:
- (AR+BR)+(CT+DT)+(EU+FW)=AB+CD+EF
- And for the right side:
- (BS+CS)+(DU+EU)+(AW+FW)=BC+DE+FA
- Thus, we have:
AB+CD+EF=BC+DE+FA
- This completes the proof.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.3 SHORT ANSWER TYPE QUESTIONS10videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Long Answer Type Questions10videos
ARITHMETIC PROGRESSIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions7videos
CONSTRUCTIONS
Similar Questions
In a hexagon ABCDEF circumscribe a circle, prove that AB+CD+EF=BC+DE+FA.
View SolutionIn Figure, a quadrilateral ABCD is drawn to circumscribe a circle .
Prove that
AB+CD=BC+AD
 View Solution
View SolutionIn Figure, a quadrilateral ABCD is drawn to circumscribe a circle .
Prove that
AB+CD=BC+AD
 View Solution
View SolutionA quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB+CD=AD+BC.
or
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB+CD=BC+DA.View SolutionIf ABCDEF is a regular hexagon, prove that AD+EB+FC=4AB.
View SolutionIf the sides of a quadrilateral ABCD touch a circle prove that
AB+CD=BC+AD.View SolutionIf a parallelogram circumscribes a circle then prove that it must be a rhombus.
 View Solution
View SolutionIn figure ΔABC is circumscribing a circle. Find the length of BC
View Solution△ABC is an isosceles triangle in which AB=AC, circumscribed about a circle. Prove that the base is bisccted by the point of contact.
View SolutionThe given figure shows an isosceles triangle ABC inscribed in a circle such that AB=AC. If DAE is a tangent to the circle at point A, prove that DE is parallel to BC.
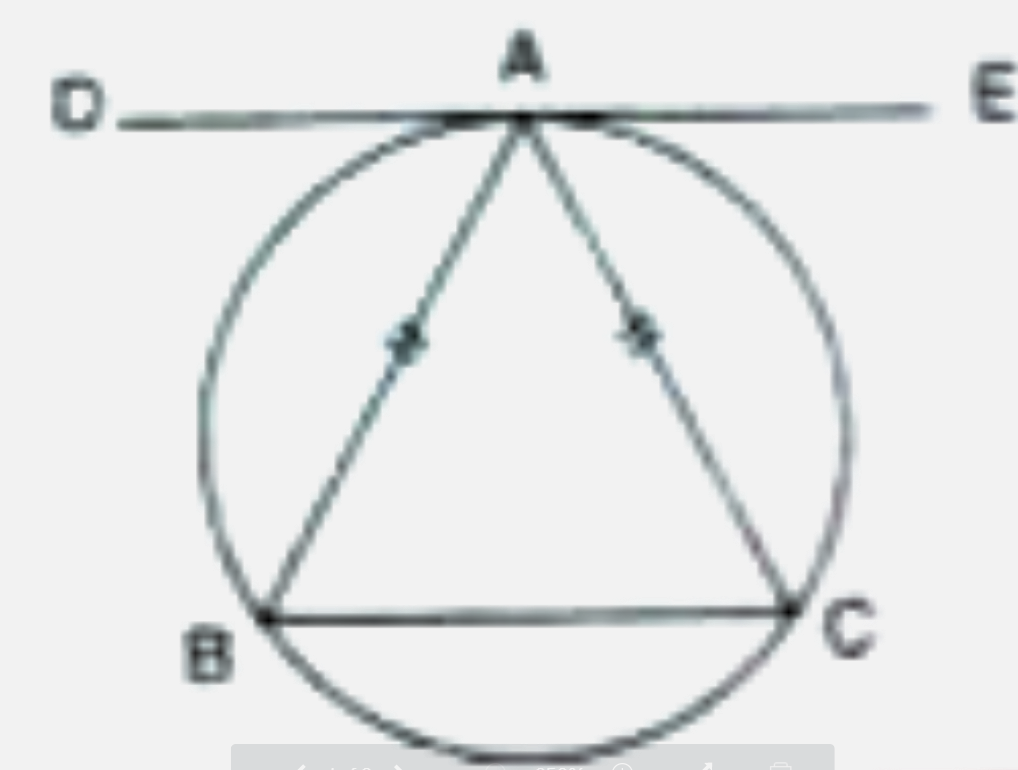 View Solution
View Solution

