Draw an isosceles triangle ABC in which AB=AC= 6 cm and BC=5 cm. Construction a triangle POR similar to $Δ A B C$ in which PQ=8 cm. Also justify the construction.

Text Solution

Verified by Experts

Let $Δ P Q R$ and $Δ A B C$ are similar triangles, the its scale factor between the corresponding sides is $\frac{P Q}{A B} = \frac{8}{6} = \frac{4}{3}$ .
Steps of construction
1. Draw a line segment BC=5cm.
2. Construct OQ the perpendicular bisector of line segment BC meeting BC at P'.
3. Taking B and C as centre draw two arcs of equal radius 6 cm intersecting each other at A
Join BA and CA. So., $Δ A B C$ is the required isosceles triangle

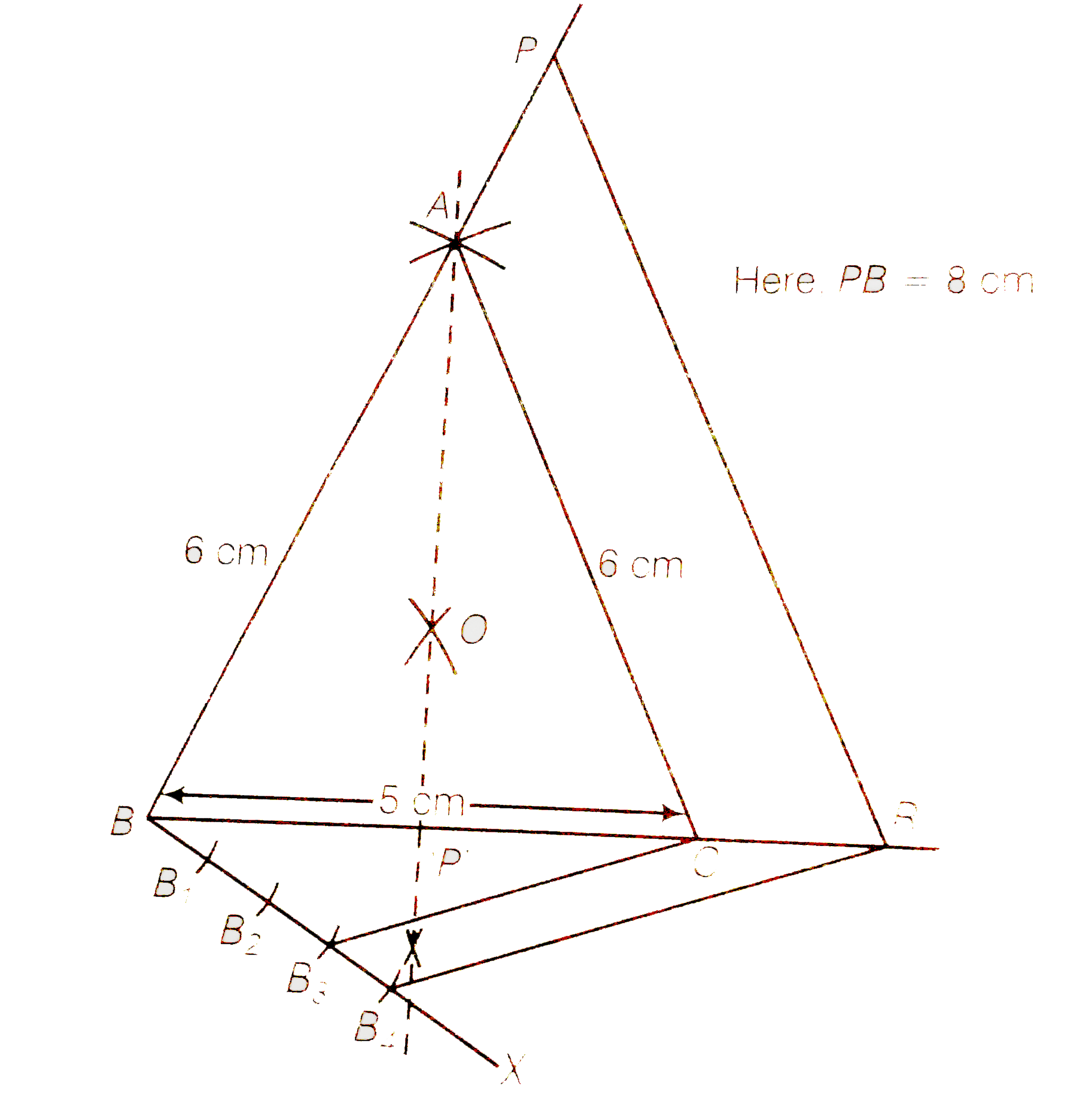
5 From, draw any ray BX making an acute $∠ C B X$ .
6. Locate four points $B_{1}, B_{2}, B_{3} and B_{4}$ on BX such that $B B_{1} = B_{1} B_{2} = B_{2} B_{3} = B_{3} B_{4}$ .
Join $B_{3} C$ and from $B_{4}$ draw a line $B_{4} R ∣ ∣ B_{3} C$ intersecting the extended line segment BC at R.
8. From point R, draw $R P ∣ ∣ C A$ meeting BA produced at P.
Then $Δ P B R$ is the required triangle.
Justification
$∴ B_{4} R ∣ ∣ B_{3} C$ ( by construction )
$∴ \frac{B C}{C R} = \frac{3}{1}$
$N o w, \frac{B R}{B C} = \frac{B C + C R}{B C}$
$= 1 + \frac{C R}{B C} = 1 + \frac{1}{3} = \frac{4}{3}$
Also, RP||CA
$∴ Δ A B C ~ Δ P B R$
and $\frac{P B}{A B} = \frac{R P}{C A} = \frac{B R}{B C} = \frac{4}{3}$
Hence, the new triangle is similar to the given triangle whose sides are $\frac{4}{3}$ times of the corresponding sides of the isosceles $Δ A B C$ .

|

Updated on:21/07/2023

Class 10 MATHS CONSTRUCTIONS

Topper's Solved these Questions

Similar Questions

NCERT EXEMPLAR ENGLISH-CONSTRUCTIONS-Exercise 10.4 Long Answer type Questions

Home
Ask Doubt
Profile