Find the equations the sides of an isosceles right angled triangle the equation of whose hypotenuse is 3x+4y=4 and the opposite vertex is the point (2, 2).
The correct Answer is:N/a
Let slope of line AC be m and slope of line BC is −34 and let angle between line AC and BC be θ
∴tanθ=∣∣
∣∣m+341−3m4∣∣
∣∣⇒tan45∘=±⎡⎣m+341−3m4⎤⎦
Taking positive sign, 1=m+341−3m4
⇒m+34=1−3m4
⇒m+3m4=1−34
⇒7m4=14⇒m=17
Taking negative sign, 1=m+341−3m4
⇒m+34=1−3m4
⇒m+3m4=1−34
⇒7m4=14⇒m=17
Taking negative sign,
1=⎛⎝m+341−3m4⎞⎠⇒1−3m4=−m−34
⇒m−3m4=−1−34
⇒3m4=−74⇒m=−7
∴ Equation of side AC having slope (17) is
y−2=17(x−2)
⇒7y−14=x−2
⇒x−7y+12=0
and equation of side AB having slope (−7) is
y−2=−7(x−2)
⇒y−2=−7x+14
⇒7x+y−16=0
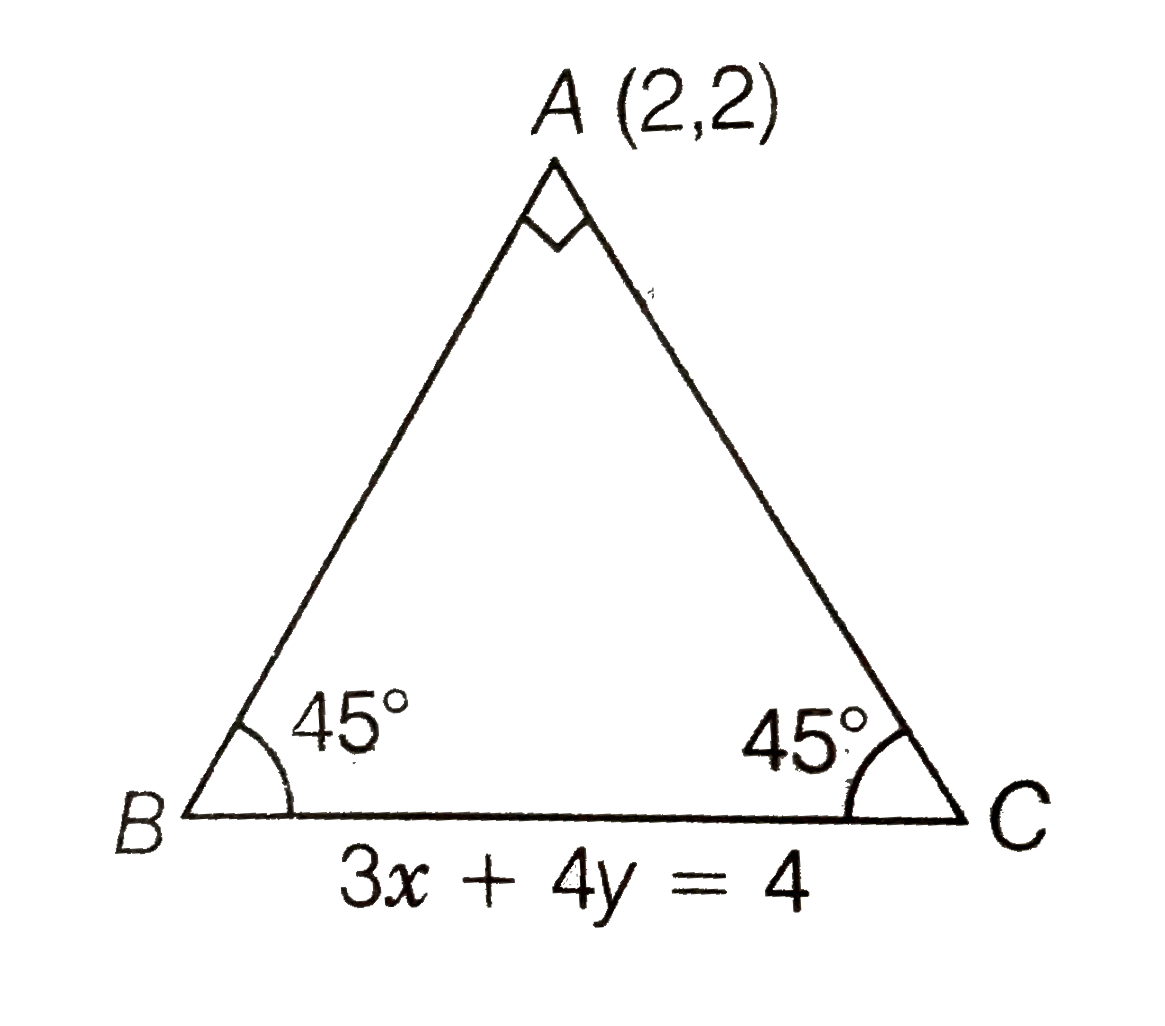
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Long Answer type9videos
STRAIGHT LINES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Objective type questions20videos
STRAIGHT LINES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICSEXERCISE - FILLERS7videos
STATISTICS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - TRUE/FALSE9videos
TRIGONOMETRIC FUNCTIONS
Similar Questions
Find the equations of the sides of an isosceles right angled triangle the equation of whose hypotenuse is 3x+4y=4 and the opposite vertex is the point (2, 2).
View SolutionFind the equation of one of the side of an isosecles right angled triangle whose hypotenuse is given by 3x + 4y = 4 and the opposite vertex of the hypotenuse is (2,2).
View SolutionFind the equation of the legs of a right isosceles triangle if the equation of its hypotenuse is x−2y−3=0 and the vertex of the right angle is at the point (1,6),
View SolutionFind the locus of the third vertex of a right angled triangle , the ends of whose hypotenuse are (4,0) and (0,4)
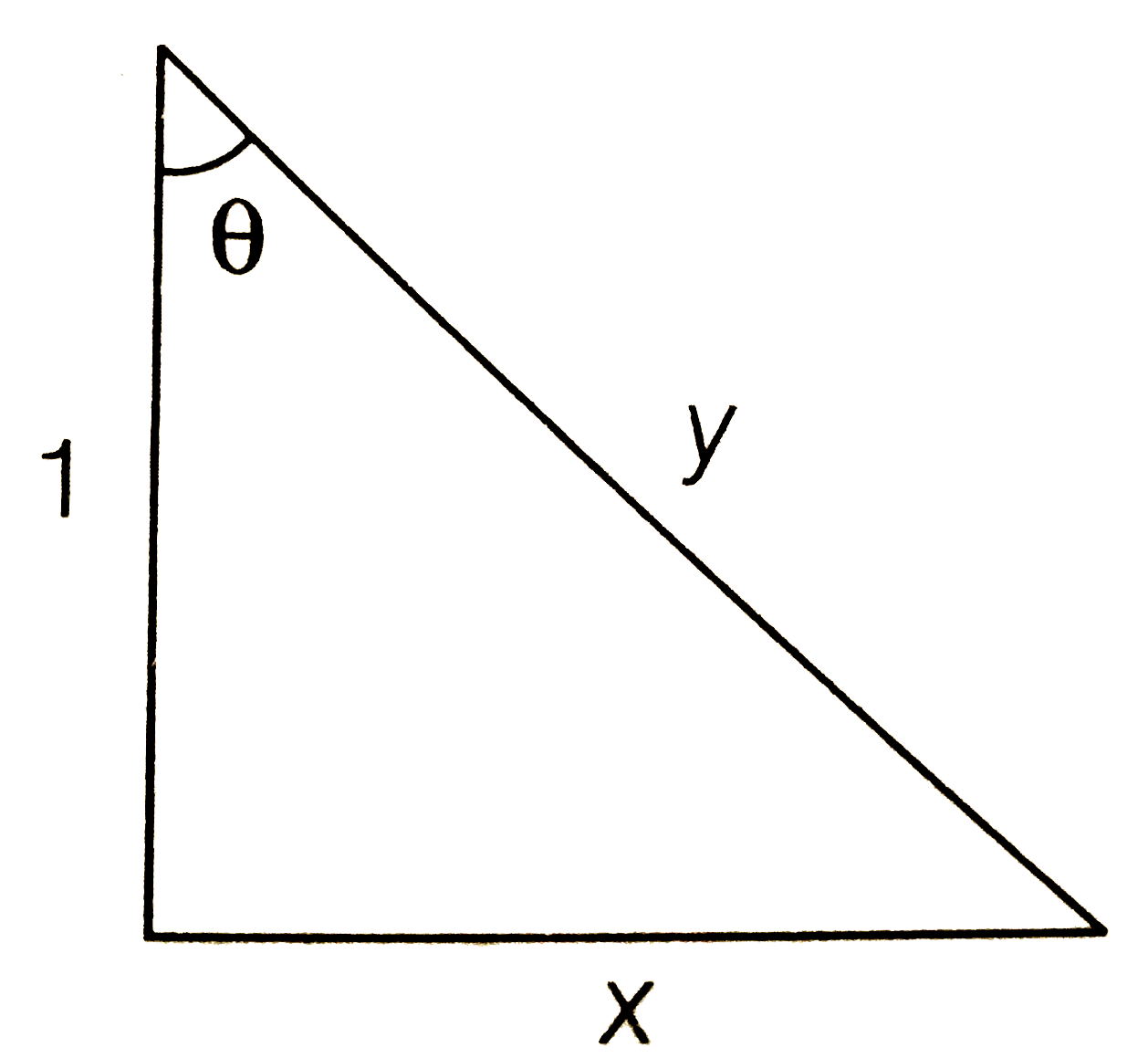
View SolutionA right angled triangle has legs 1 and x. The hypotenuse is y and angle opposite to the side x is θ. Shown as
 View Solution
View SolutionFind the equations of the medians of a triangle, the equations of whose sides are : 3x+2y+6=0, 2x−5y+4=0 and x−3y−6=0.
View SolutionFind the equations of the medians of a triangle, the equations of whose sides are: 3x+2y+6=0, 2x−5y+4=0 and x−3y−6=0
View SolutionThe ends of the base of an isosceles triangle are at (2a,0)and(0,a). The equation of one side is x=2a.The equation of the other side, is
View SolutionDraw a right angled isosceles triangle whose hypotenuse is 5.2 cm long.
View SolutionFind the centre of the inscribed circle of the triangle the equations, of whose sides are y−15=0,12y+5x=0and4y−3x=0.
View Solution

