If →a+→b+→c=0, then show that →a×→b=→b×→c=→c×→a. Interpret the result geometrically.
Text Solution
Since, →a+→b+→c=0
⇒→b=−→c−→a
Now, →a×→b×=→a×(−→c−→a)
=→a×(−→c)+→a×(−→a)=−→a×→c
⇒→a×→b=→c×→a.....(i)
Also, →b×→c=(−→c−→a)×→c
=(−→c×→c)+(−→a×→c)=−→a×→c
⇒→b×→c=→c×→a......(ii)
From Eqs. (i) and (ii), →a×→b=→b×→c=→c×→a
Geometrical interpretation of the result
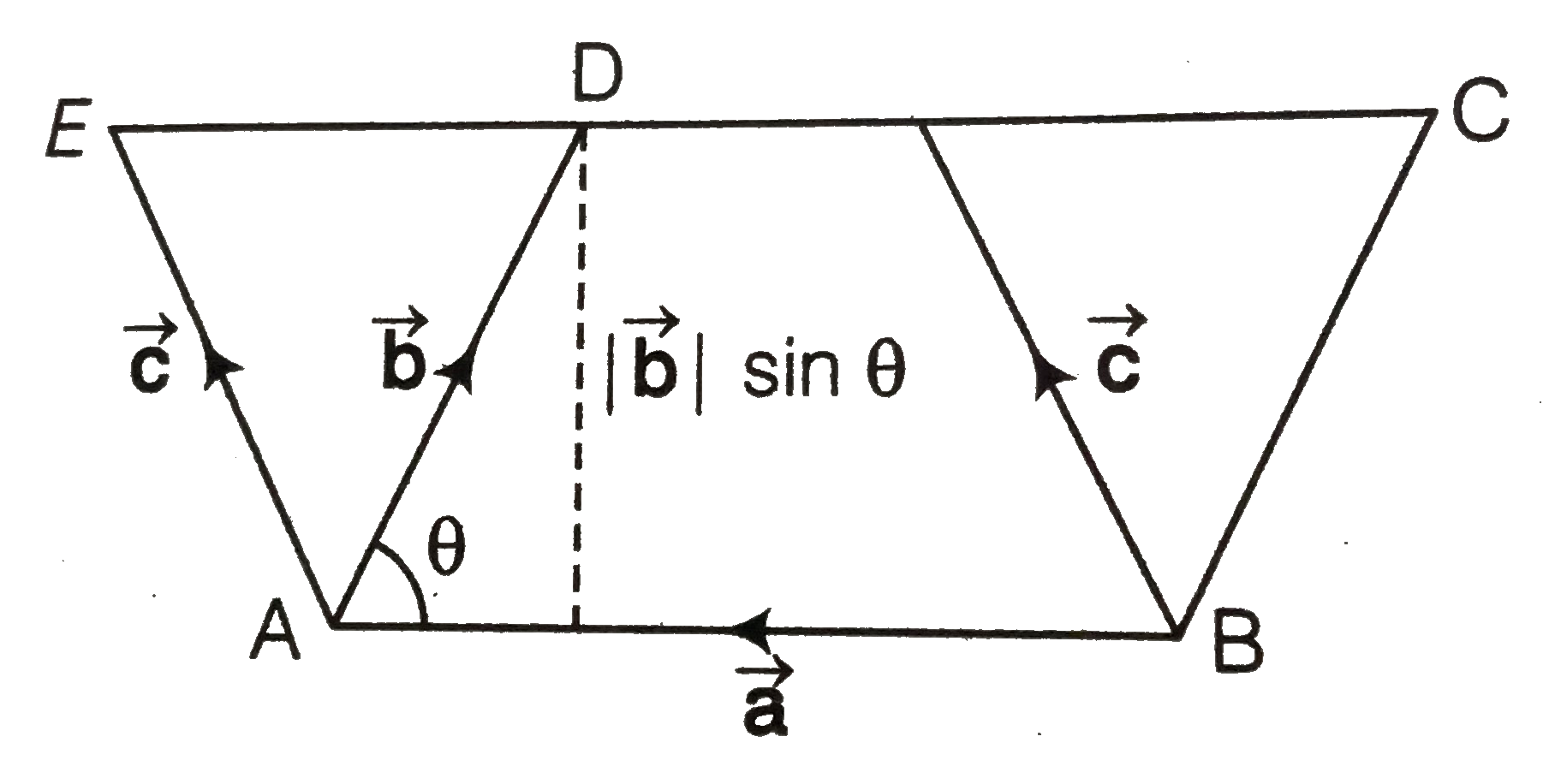
If ABCD is a parallelogram such that −−→AB=→aand−−→AD=→b and these adjacent sides are making angle θ between each other then we say that
Area of parallelogram ABCD=|→a|∣∣→b∣∣|sinθ|=∣∣→a×→b∣∣ Since, parallelogram on the same base and between the same parallels are equal in area.
We can say that, ∣∣→a×→b∣∣=|→a×→c|=∣∣→b×→c∣∣
This also implies that, →a×→b=→a×→c=→b×→c
So, area of the parallelograms formed by taking any two sides represented by →a,→band→c as adjacent are equal.
|
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - NCERT EXEMPLAR ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - LONG ANSWER TYPE QUESTIONS
4 Videos
- VECTOR ALGEBRABOOK - NCERT EXEMPLAR ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - OBJECTIVE TPYE QUESTIONS
27 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - LONG ANSWER TYPE QUESTIONS
16 Videos
Similar Questions
Knowledge Check
If →a,→b,→c are three vectors, then
[→a×→b→b×→c→c×→a]=A[→a→b→c]B2[→a→b→c]C3[→a→b→c]D[→a→b→c]2If 4→a+5→b+9→c=→0 then (→a×→b).{(→b×→c)×(→c×→a)} is equal to
A→0B→aC→bD→cIf 4→a+5→b+9→c=0 then (→a×→b)×[(→b×→c)×(→c×→a)] is equal to
Aa vector perpendicular to the plane of →a,→band→cBa scalar quantityC→0Dnone of these
If →a+2→b+3→c=0, then →a×→b+→b×→c+→c×→a=
View SolutionIf →a,→b,→c are three vectors, then
[→a×→b→b×→c→c×→a]=
View SolutionIf →a,→b,→c are coplanar then show that →a×→b,→b×→cand→c×→a are also coplanar.
View SolutionIf →a,→b,→c are coplanar then show that →a×→b,→b×→cand→c×→a are also coplanar.
View SolutionIf 4→a+5→b+9→c=0 then (→a×→b)×[(→b×→c)×(→c×→a)] is equal to
View Solution
