If $\vec{a} + \vec{b} + \vec{c} = 0$ , then show that $\vec{a} \times \vec{b} \times \vec{c} = \vec{c} \times \vec{a}$ . Interpret the result geometrically.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:Since, $\vec{a} + \vec{b} + \vec{c} = 0$
$\Rightarrow \vec{b} = - \vec{c} - \vec{a}$
Now, $\vec{a} \times \vec{b} \times = \vec{a} \times (- \vec{c} - \vec{a})$
$= \vec{a} \times (- \vec{c}) + \vec{a} \times (- \vec{a}) = - \vec{a} \times \vec{c}$
$\Rightarrow \vec{a} \times \vec{b} = \vec{c} \times \vec{a} ... . . (i)$
Also, $\vec{b} \times \vec{c} = (- \vec{c} - \vec{a}) \times \vec{c}$
$= (- \vec{c} \times \vec{c}) + (- \vec{a} \times \vec{c}) = - \vec{a} \times \vec{c}$
$\Rightarrow \vec{b} \times \vec{c} = \vec{c} \times \vec{a} ... ... (i i)$
From Eqs. (i) and (ii), $\vec{a} \times \vec{b} = \vec{b} \times \vec{c} = \vec{c} \times \vec{a}$
Geometrical interpretation of the result

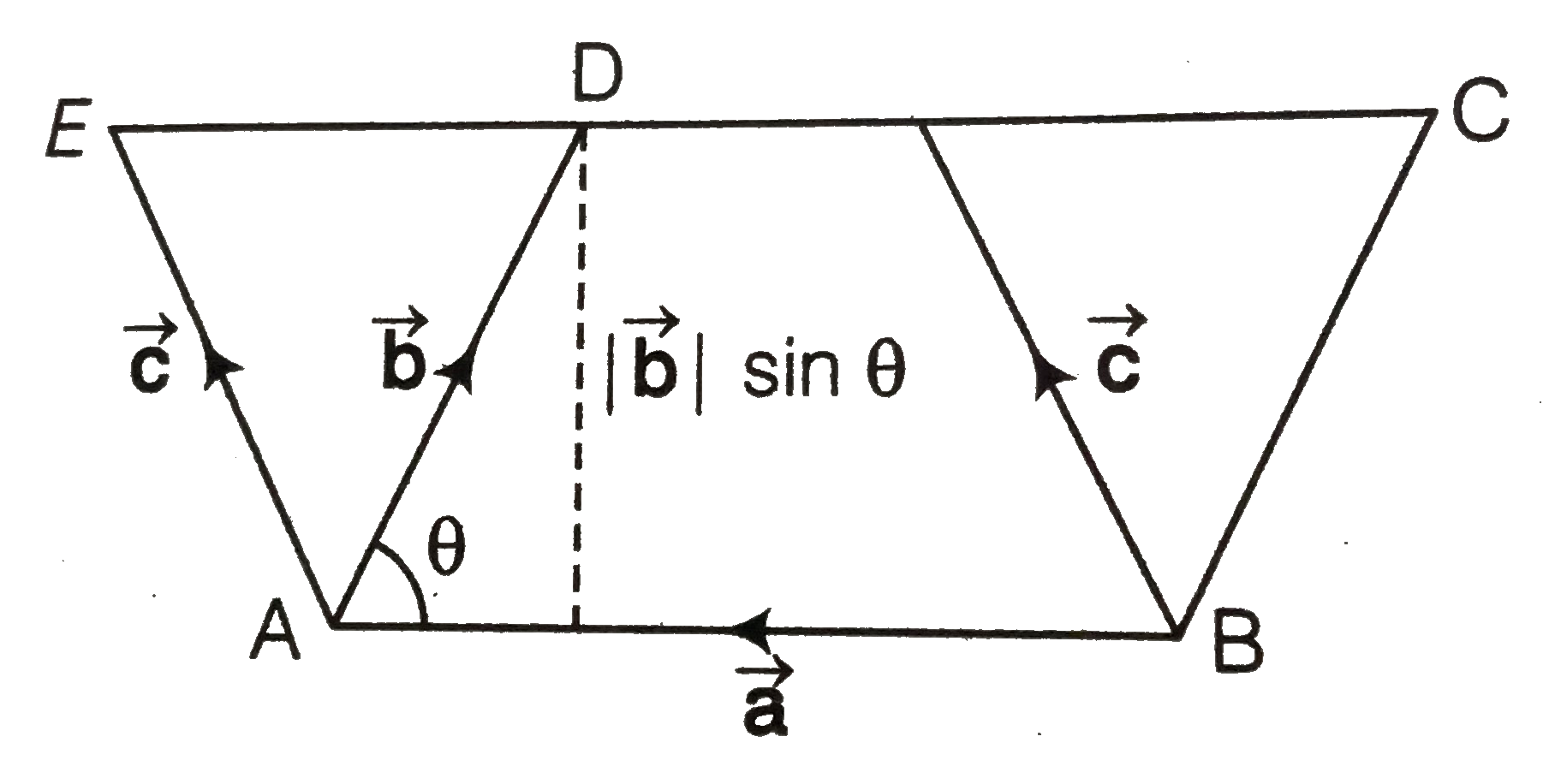
If ABCD is a parallelogram such that $\vec{A B} = \vec{a} and \vec{A D} = \vec{b}$ and these adjacent sides are making angle $θ$ between each other then we say that
Area of parallelogram $A B C D = | \vec{a} | | \vec{b} | | \sin θ | = | \vec{a} \times \vec{b} |$ Since, parallelogram on the same base and between the same parallels are equal in area.
We can say that, $| \vec{a} \times \vec{b} | = | \vec{a} \times \vec{c} | = | \vec{b} \times \vec{c} |$
This also implies that, $\vec{a} \times \vec{b} = \vec{a} \times \vec{c} = \vec{b} \times \vec{c}$
So, area of the parallelograms formed by taking any two sides represented by $\vec{a}, \vec{b} and \vec{c}$ as adjacent are equal.

Since, $\vec{a} + \vec{b} + \vec{c} = 0$
$\Rightarrow \vec{b} = - \vec{c} - \vec{a}$
Now, $\vec{a} \times \vec{b} \times = \vec{a} \times (- \vec{c} - \vec{a})$
$= \vec{a} \times (- \vec{c}) + \vec{a} \times (- \vec{a}) = - \vec{a} \times \vec{c}$
$\Rightarrow \vec{a} \times \vec{b} = \vec{c} \times \vec{a} ... . . (i)$
Also, $\vec{b} \times \vec{c} = (- \vec{c} - \vec{a}) \times \vec{c}$
$= (- \vec{c} \times \vec{c}) + (- \vec{a} \times \vec{c}) = - \vec{a} \times \vec{c}$
$\Rightarrow \vec{b} \times \vec{c} = \vec{c} \times \vec{a} ... ... (i i)$
From Eqs. (i) and (ii), $\vec{a} \times \vec{b} = \vec{b} \times \vec{c} = \vec{c} \times \vec{a}$
Geometrical interpretation of the result

If ABCD is a parallelogram such that $\vec{A B} = \vec{a} and \vec{A D} = \vec{b}$ and these adjacent sides are making angle $θ$ between each other then we say that
Area of parallelogram $A B C D = | \vec{a} | | \vec{b} | | \sin θ | = | \vec{a} \times \vec{b} |$ Since, parallelogram on the same base and between the same parallels are equal in area.
We can say that, $| \vec{a} \times \vec{b} | = | \vec{a} \times \vec{c} | = | \vec{b} \times \vec{c} |$
This also implies that, $\vec{a} \times \vec{b} = \vec{a} \times \vec{c} = \vec{b} \times \vec{c}$
So, area of the parallelograms formed by taking any two sides represented by $\vec{a}, \vec{b} and \vec{c}$ as adjacent are equal.

|

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

BOOK - NCERT EXEMPLARCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Three Dimensional Geometry
46videos
THREE DIMENSIONAL GEOMETRY

Similar Questions

Knowledge Check

Question 1 - Select One
If $\to a, \to b, \to c$ are three vectors, then
$[\begin{matrix} \to a \times \to b & \to b \times \to c & \to c \times \to a \end{matrix}] =$
A $[\begin{matrix} \to a & \to b & \to c \end{matrix}]$
B $2 [\begin{matrix} \to a & \to b & \to c \end{matrix}]$
C $3 [\begin{matrix} \to a & \to b & \to c \end{matrix}]$
D ${[\begin{matrix} \to a & \to b & \to c \end{matrix}]}^{2}$
Question 2 - Select One
If $\to A + \to B + \to C = 0$ , then $\to A \times \to B$ is
A $\to B \times \to C$
B $\to C \times \to B$
C $\to A \times \to C$
DNone of these
Question 3 - Select One
If $4 \to a + 5 \to b + 9 \to c = \to 0$ then $(\to a \times \to b) . {(\to b \times \to c) \times (\to c \times \to a)}$ is equal to
A $\to 0$
B $\to a$
C $\to b$
D $\to c$

NCERT EXEMPLAR-VECTOR ALGEBRA-Vector Algebra

Home
Ask Doubt
Profile