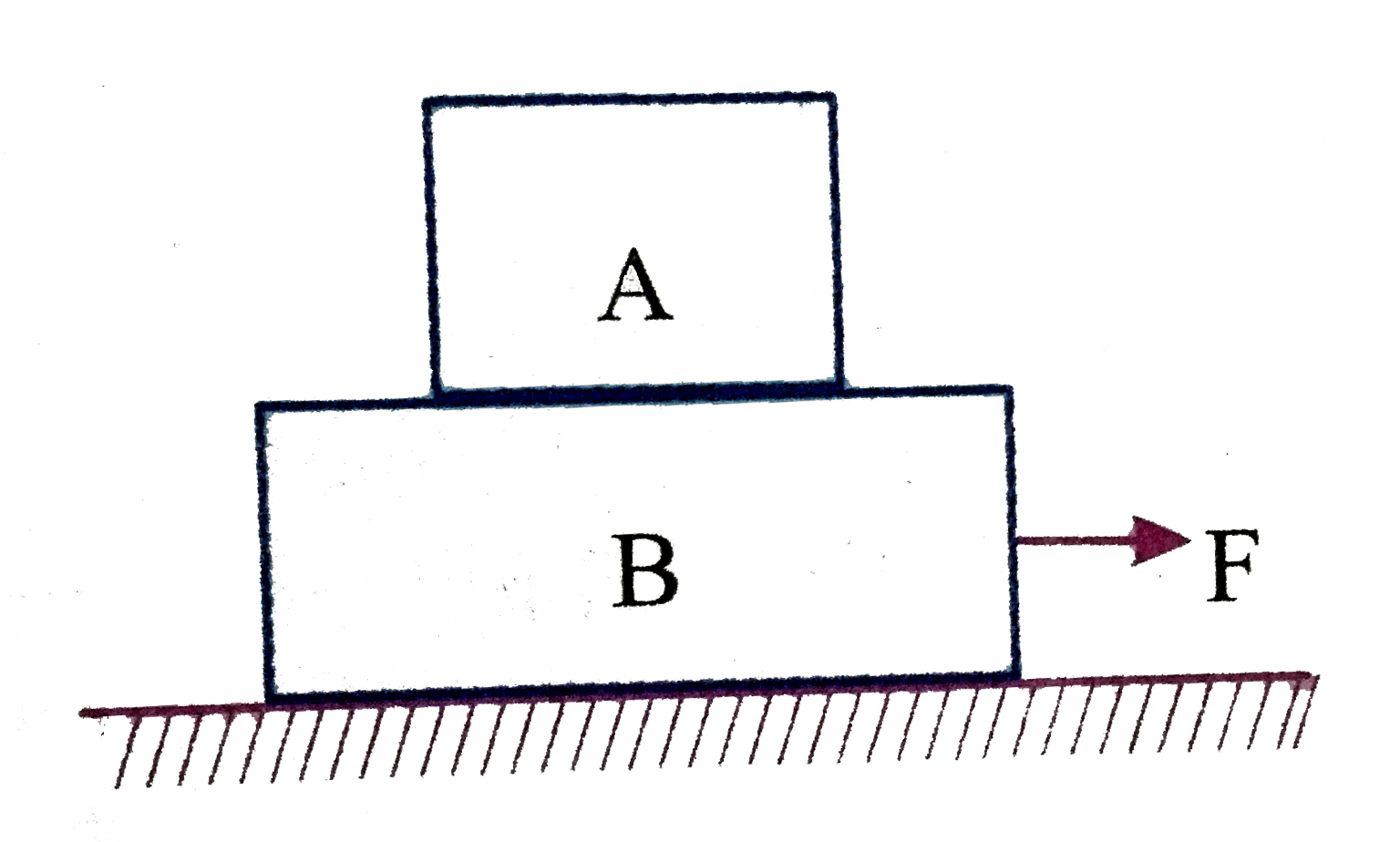
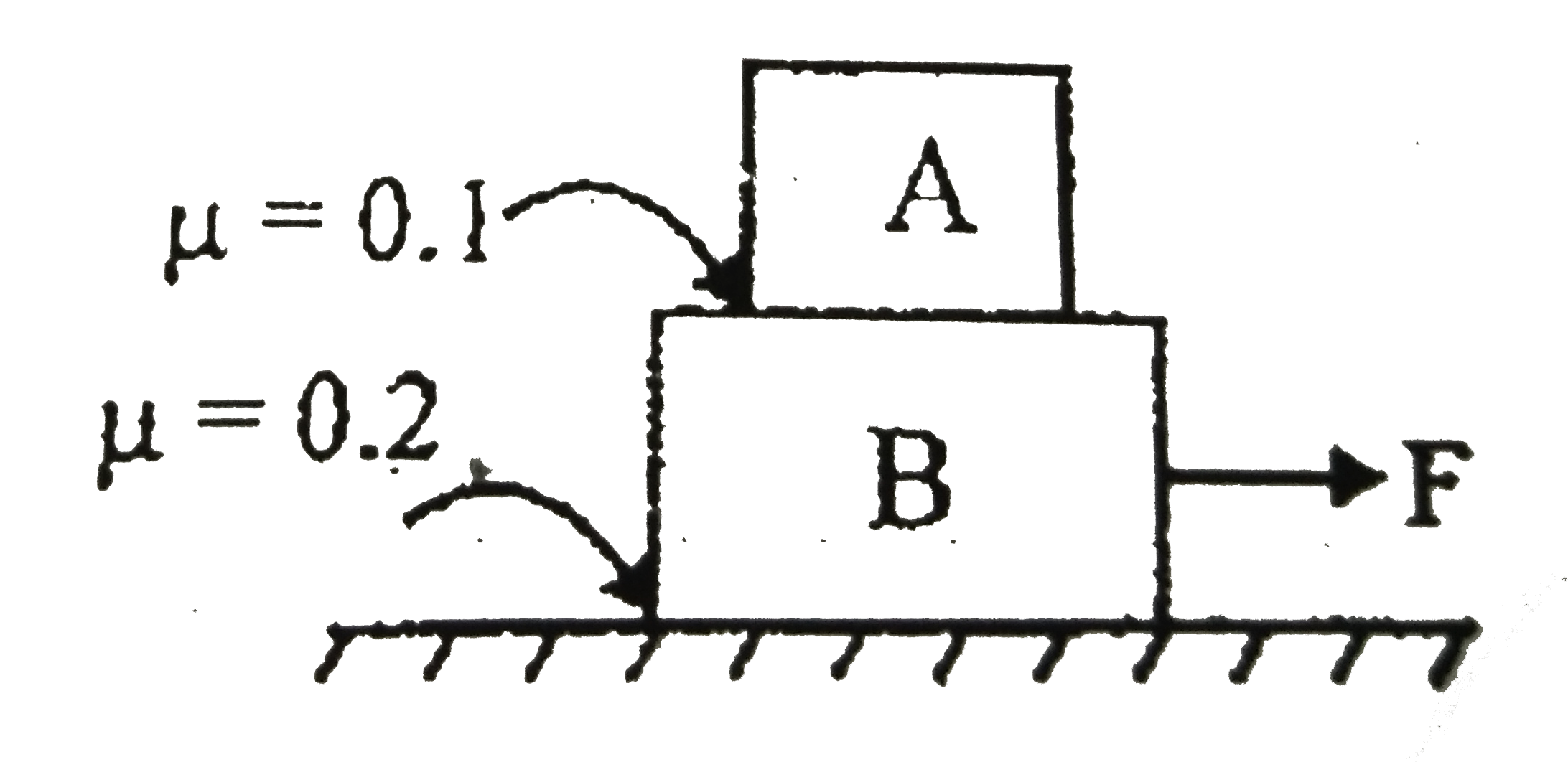
In the co-efficinet of friction between the floor and the body B is 0.1. The co-efficient of friction beteen the bodies B and A is 0.2 A fore F is applied as shown B The mass of A is m/2 and of B is m Which of the following statements are ture ?
 .
.
The bodies will move together if F = 0.25 mg
The body A will slip with respect to B if F = 0.5 mg
The bodies will be rest if F = 0.1 mg
The maximum value of F for which the two bodies will move together is 0.45 mg
The correct Answer is:A, B, D
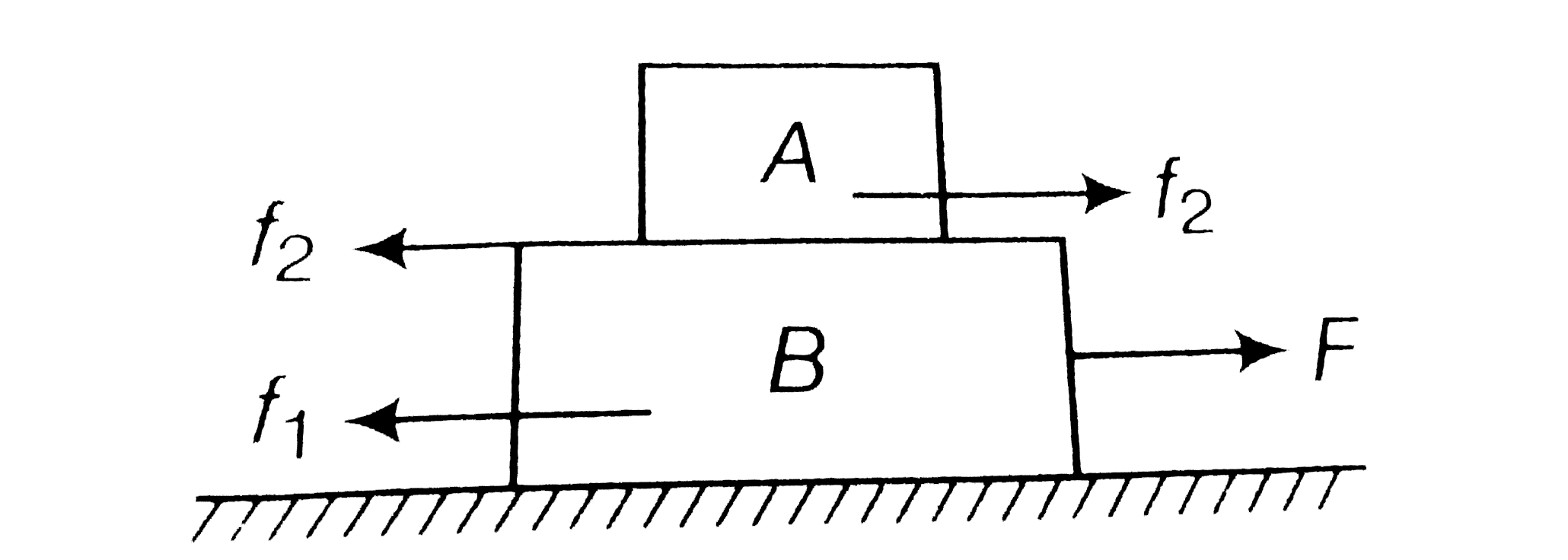
Consider the adjacent diagram . Frictional force on B(f1) and frictional force on A (f2) will be as shown.
Let A and B are moving together acommon=F−f1mA+mB=F−f1(m/2)+m=2(F−f1)3m
Pseudo force on A = (mA)×acommon
=mA×2(F−f1)3m=m2×2(F−f1)3m=(F−f1)3
The force (F) will be maximum when
Pseudo force on A = Frictional force on A
⇒ Fmax−f13=μmAg
= 0.2×m2×g=0.1 mg
⇒ Fmax=0.3mg+f1
=0.3 mg + (0.1)32mg=0.45 mg
⇒ Hence , maximum force upto which bodies will move together is Fmax=0.45 mg
(a) Hence for F = 0.25 mg <Fmax bodies will move together .
(b) For F = 0.5mg>Fmax , body A will slip with respect to B .
(c) For F = 0.5 mg >Fmax , bodies slip
(f1)max=μMBg=(0.1)×32m×g=0.15 mg
(f2)max=μmAg=(0.2)(m2)(g)=0.1 mg
Hence , minimum force required for movement of the system (A + B)
Fmin=(f1)max+(f2)max
= 0.15 mg + 0.1 mg = 0.25 mg
(d) Given , force F = 0.1 mg <Fmin
Hence , the bodies will be at rest .
(e) Maximum force for combined movement Fmax=0.45 mg .
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Very short answer type Questions12videos
LAWS OF MOTION
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Short answer type questions6videos
LAWS OF MOTION
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Long answer Type Questions9videos
LAWS OF MOTION
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Multiple Choice Questions (MCQs)31videos
KINETIC THEORY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Long Answer Type Questions3videos
MECHANICAL PROPERTIES OF FLUIDS
Similar Questions
The block each of mass 1kg are placed as shown .They are connected by a string which passes over a smooth (massless) pulley.

There is no friction between m1 and the ground.The coefficient of friction between m1 andm2 is 0.2A force F is applied to m2. Which of the fpllowing statement is/are correct?View SolutionIn the figure shown co-efficient of friction between the block B and C is 0.4. There is no friction between the block C and hte surface on which it is placed. The system of blocks is released from rest in the shown situation. Find the distance moved by the block C when block A descends through a distance 2m. Given masses of the blocks are mA=3kg,mB=5kgandmC=10kg.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the co-efficinet of friction between the floor and the body B is 0.1. The co-efficient of friction beteen the bodies B and A is 0.2 A fore F is applied as shown B The mass of A is m/2 and of B is m Which of the following statements are ture ?
 .AThe bodies will move together if F=0.25mgBThe body A will slip with respect to B if F=0.5mgCThe bodies will be at rest if F=0.5mgDThe maximum value of F for which the two bodies will move together is 0.45mg
.AThe bodies will move together if F=0.25mgBThe body A will slip with respect to B if F=0.5mgCThe bodies will be at rest if F=0.5mgDThe maximum value of F for which the two bodies will move together is 0.45mg - Question 2 - Select One or More
The block each of mass 1kg are placed as shown .They are connected by a string which passes over a smooth (massless) pulley.

There is no friction between m1 and the ground.The coefficient of friction between m1 andm2 is 0.2A force F is applied to m2. Which of the fpllowing statement is/are correct?AThe system will be in equilibrium if F≤4NBF≥4N tension in the string will be 4NCF≥4N the frictional force between the blocks will be 2NDF=6N tension in the string will be 3N - Question 3 - Select One
The coefficient of friction between the block A of mass m & block B of mass 2m is μ. There is no friction between A&B is released from rest & there is no slipping between A&B then:
 A2θ≤sin−1(2μ)Bθ≤tan−1(μ)C2θ≤cos−1(2μ)D2θ≤tan−1(μ/2)
A2θ≤sin−1(2μ)Bθ≤tan−1(μ)C2θ≤cos−1(2μ)D2θ≤tan−1(μ/2)
In the figure shown co-efficient of friction between the block B and C is 0.4. There is no friction between the block C and hte surface on which it is placed. The system of blocks is released from rest in the shown situation. Find the distance moved by the block C when block A descends through a distance 2m. Given masses of the blocks are mA=3kg,mB=5kgandmC=10kg.
 View Solution
View SolutionIn the figure shown, the coefficient of friction between the two blocks is 0.1 and coefficient of friction between the block B and ground is 0.2, masses of A and B are 20kg and 40kg respectively. where aA= acceleration of A and aB= acceleration of B.
Column IColumn II(A)F=50N(P)aA=0m/s2(B)F=150N(Q)aA=0.5m/s2(C)F=200N(R)aB=0.5m/s2(S)aB=1.5m/s2View SolutionIn the figure masses m1,m2andM are 20 kg, 5 kg and 50 kg, respectively. The co-efficient of friction between M and ground is zero. The co-efficient of friction between m1andM and that between m2 and ground is 0.3. The pulleys and the string are massless.
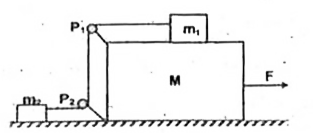
The string is perfectly horizontal between P1 and m1 and also between P2andm2. The string is perfectly vertical between P1andP2. An external horizontal force F is applied to the mass M. Take g=10m/s2.
(a) Draw a free body diagram for mass M, clearly showing all the forces.
(b) Let the magnitude of the force of friction between m1andM be f1 and that between m2 and ground be f2. For a particular F, it is found that f1=2f2. Find f1andf2. Write down equations of motion of all the masses. Find F, tension in the string and accelerations of the masses.View SolutionThe coefficient of friction between the block A of mass m and the triangular wedge B of mass M is μ. There in no friction between the wedge and the plane if the system (block A+ wedge B) is released so that there is no stiding between A and B find the inclination θ
 View Solution
View SolutionThe coefficient of friction between the block A of mass m and the triangular wedge B of mass M is μ. There in no friction between the wedge and the plane if the system (block A+ wedge B) is released so that there is no stiding between A and B find the inclination θ
 View Solution
View Solution

