What is electrical resistivity ? In a series electrical circuit comprising a resistor made up of a matallic wire, the ammeter reads 5A. The reading of the ammeter decreases to half when the length of the wire is doubled. Why ?
Step-by-Step Solution:
1. Understanding Electrical Resistivity:
- Electrical resistivity (ρ) is a property of a material that quantifies how strongly it resists the flow of electric current. It is defined as the resistance (R) of a material per unit length (L) and per unit cross-sectional area (A).
- The formula for resistance in terms of resistivity is given by:
R=ρLA
- Here, ρ is the resistivity, L is the length of the conductor, and A is the cross-sectional area.
2. Initial Conditions:
- In the given problem, we have a series electrical circuit with a metallic wire that has an ammeter reading of 5 A. This indicates the current flowing through the circuit.
3. Effect of Doubling the Length of the Wire:
- When the length of the wire is doubled (let's denote the new length as L′=2L), we need to analyze how this affects the resistance and the current.
- From the resistance formula, if the length is doubled, the new resistance R′ can be expressed as:
R′=ρ(2L)A=2⋅ρLA=2R
- This shows that the resistance doubles when the length of the wire is doubled.
4. Applying Ohm's Law:
- According to Ohm's Law, the relationship between voltage (V), current (I), and resistance (R) is given by:
V=IR
- If the voltage in the circuit remains constant, and the resistance has doubled, we can express the new current I′ as:
V=I′R′=I′(2R)
- Rearranging this gives:
I′=V2R=I2
- Since the initial current I was 5 A, the new current I′ when the length is doubled will be:
I′=5A2=2.5A
5. Conclusion:
- Therefore, when the length of the wire is doubled, the current reading on the ammeter decreases to half, resulting in a new reading of 2.5 A.
- Electrical resistivity (ρ) is a property of a material that quantifies how strongly it resists the flow of electric current. It is defined as the resistance (R) of a material per unit length (L) and per unit cross-sectional area (A).
- The formula for resistance in terms of resistivity is given by:
R=ρLA
- Here, ρ is the resistivity, L is the length of the conductor, and A is the cross-sectional area.
- In the given problem, we have a series electrical circuit with a metallic wire that has an ammeter reading of 5 A. This indicates the current flowing through the circuit.
- When the length of the wire is doubled (let's denote the new length as L′=2L), we need to analyze how this affects the resistance and the current.
- From the resistance formula, if the length is doubled, the new resistance R′ can be expressed as:
R′=ρ(2L)A=2⋅ρLA=2R
- This shows that the resistance doubles when the length of the wire is doubled.
- According to Ohm's Law, the relationship between voltage (V), current (I), and resistance (R) is given by:
V=IR
- If the voltage in the circuit remains constant, and the resistance has doubled, we can express the new current I′ as:
V=I′R′=I′(2R)
- Rearranging this gives:
I′=V2R=I2
- Since the initial current I was 5 A, the new current I′ when the length is doubled will be:
I′=5A2=2.5A
- Therefore, when the length of the wire is doubled, the current reading on the ammeter decreases to half, resulting in a new reading of 2.5 A.
Topper's Solved these Questions
Similar Questions
What is electrical resistivity ? Derive its SI unit, In a series electrical comprising a resistor made up of metallic wire, the ammeter reads , 100 mA. If the length of the wire is doubled, how will the current in the circuit change ? Justify your answer.
View SolutionIn the given figure when the key is open the ammeter reading is 5 amp. What will be the ammeter reading when the key is closed
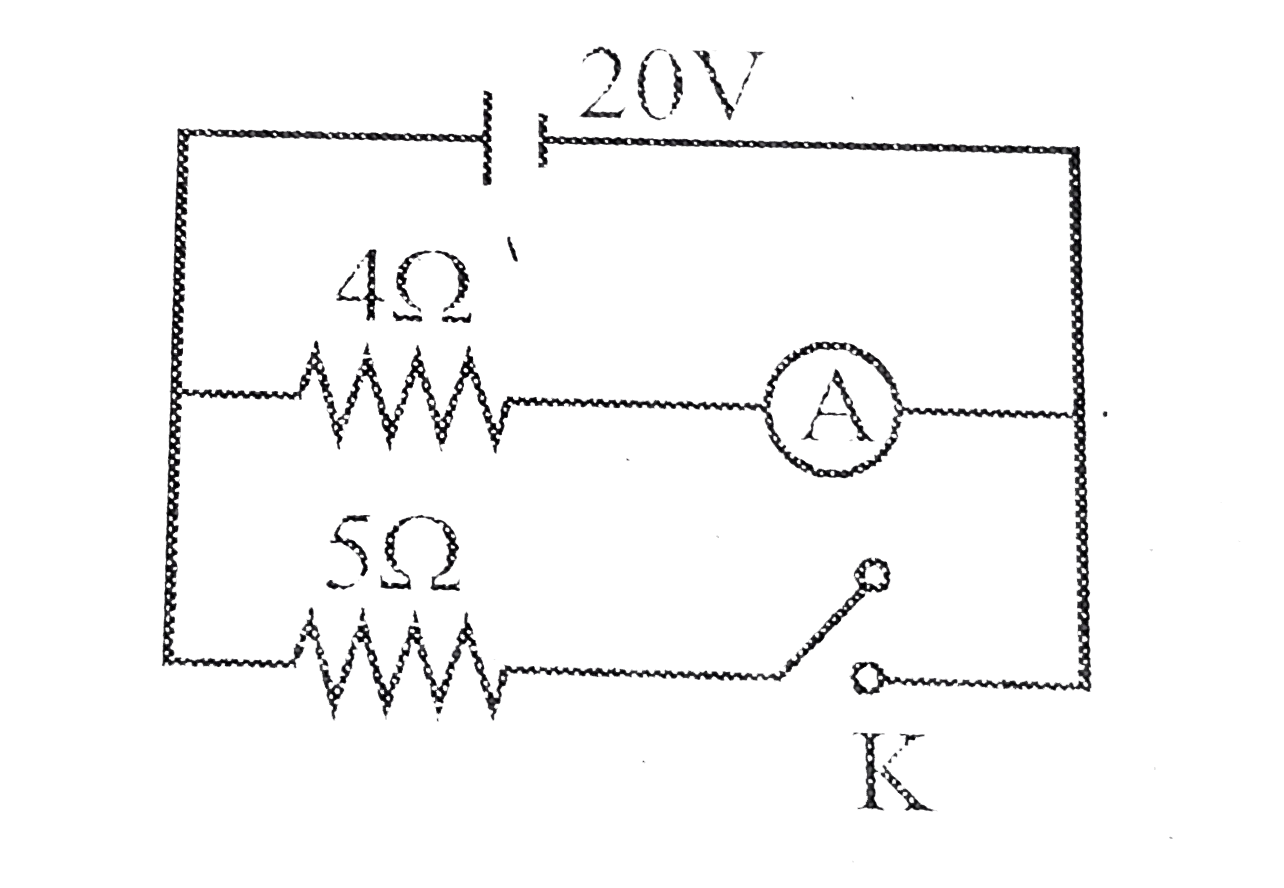
View SolutionIn the given circuit current flowing through the resistance 20Ω is 0.3A, while the ammeter reads 0.8 A. What is the value of R1

View SolutionIn the given circuit current flowing through the resistance 20Ω is 0.3A, while the ammeter reads 0.8 A. What is the value of R1

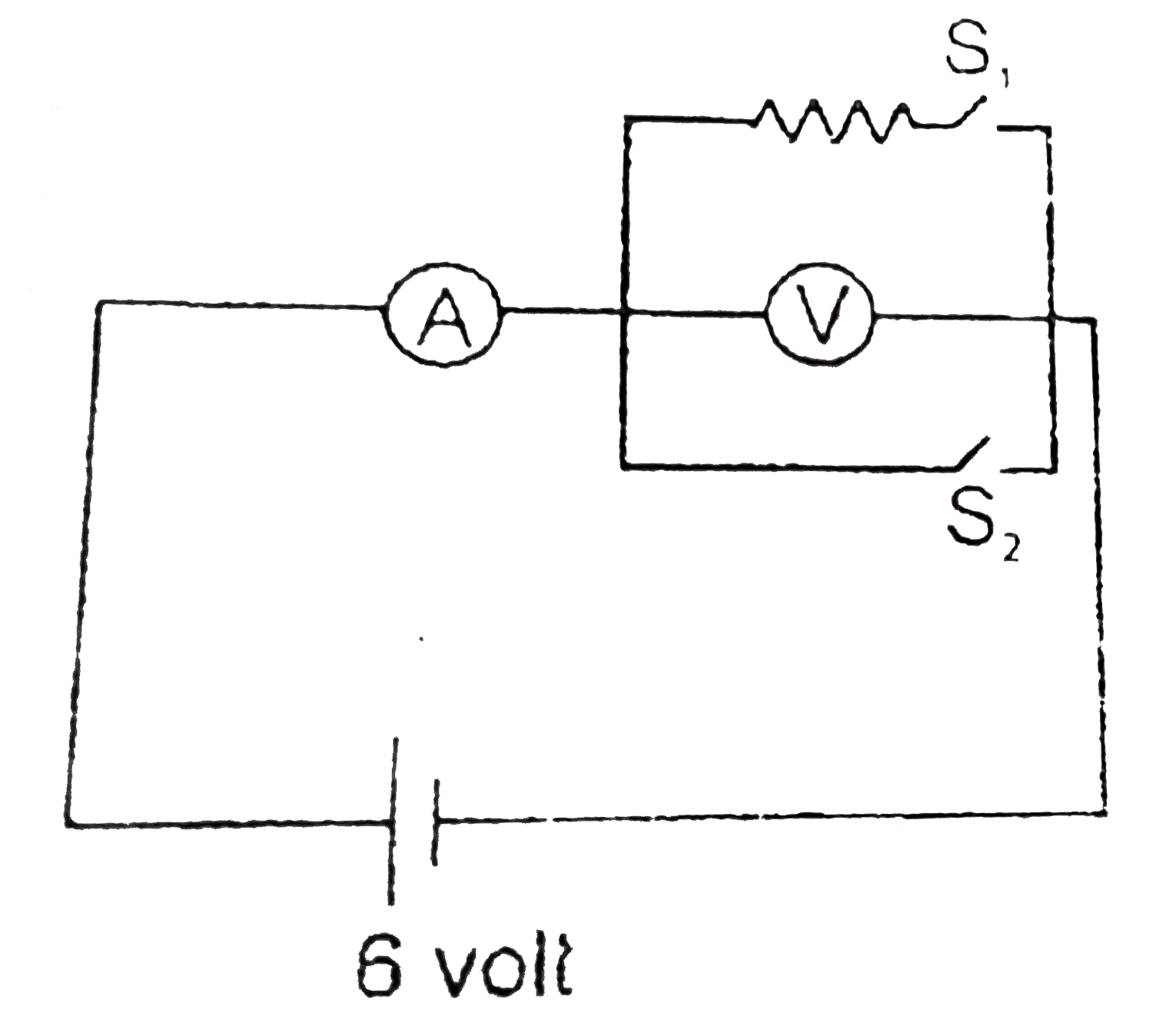
View SolutionAn ammeter and a voltmeter are initially connected in series to a battery of zero internal resistance. When switch S1 is closed the reading of the voltmeter becomes half of the initial, whereas the reading of the ammeter becomes double. If now switch S2 is also closed, then reading of ammeter becomes :
View SolutionThe figure shows a circuit.
When the circuit is switched on, the ammeter reads 0.5A.
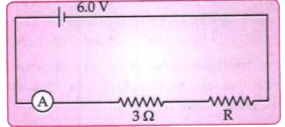
Calculate the value of the unknown resistor R.
View SolutionAn ammeter and a voltmeter are connected in series to a battery with an emf ξ=6.0V. When a certain resistance is connected in parallel with the voltmeter, the readings of the latter decreases η=2.0 times, whereas the readings of the ammeter increase the same number of times, Find the voltmeter readings after the connection of the resistance.
View SolutionThe figure shows a circuit.
When the circuit is switched on, the ammeter reads 0.5A.
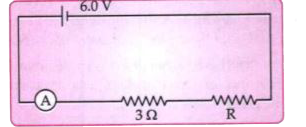
Calculate the charge passing through the 3Ω resistor in 120 s.
View SolutionIn the given LCR series circuit find the reading (in A) of the hot wire ammeter. (there all hot wire meters are ideal)
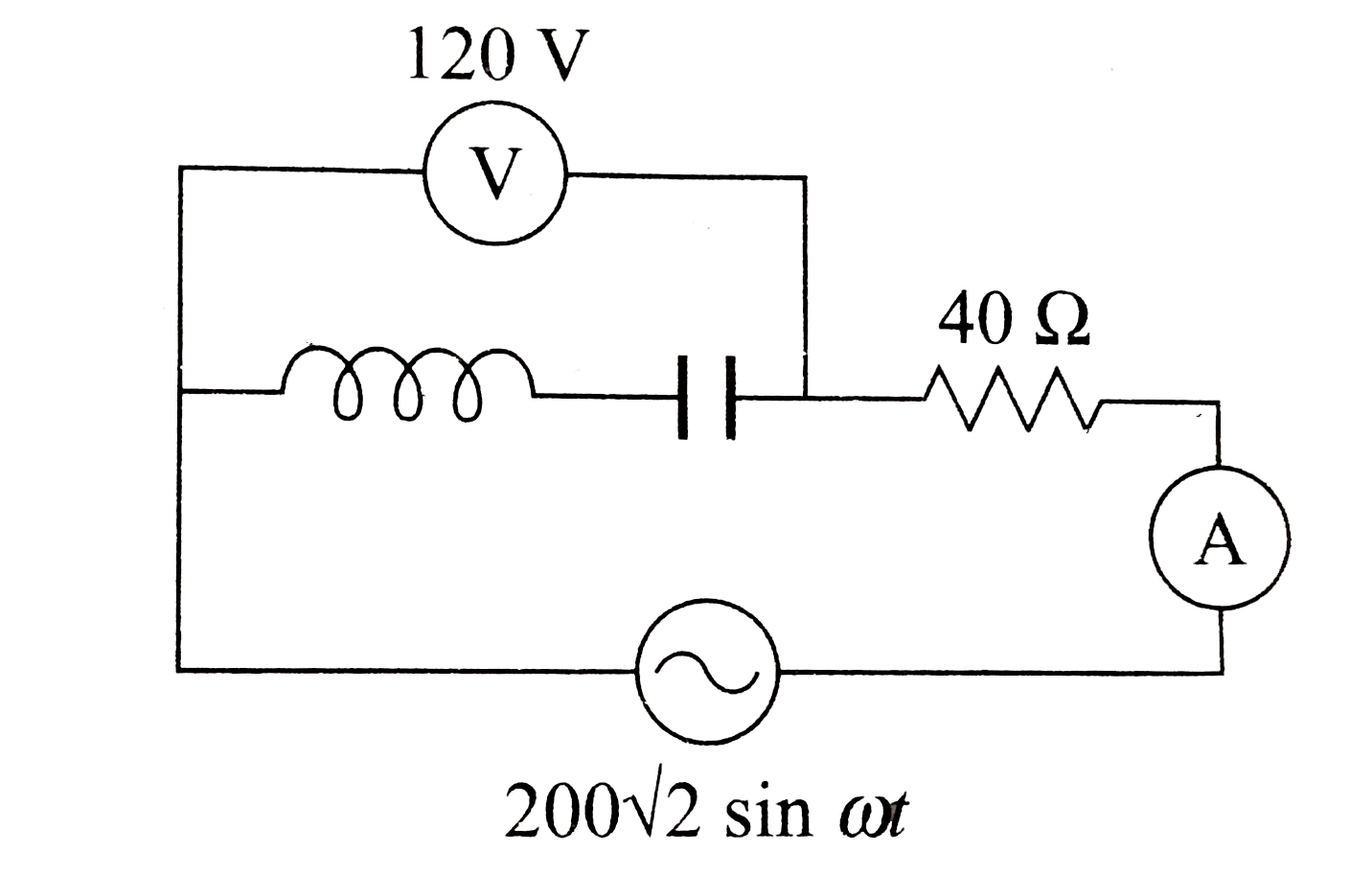
View SolutionThe figure shows a circuit.
When the circuit is switched on, the ammeter reads 0.5A.
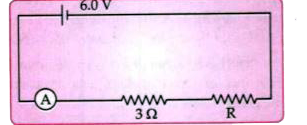
Calculate the power dissipated in the 3Ω resistor.
View Solution
