A shuttle cock used for playing badminton has the shape of the combination of
a cylinder and a sphere
a cylinder and a hemisphere
a sphere and cone
frustum of a cone and a hemisphere
The correct Answer is:D
To solve the question regarding the shape of a shuttlecock used for playing badminton, we can follow these steps:
1. Understanding the Shape of a Shuttlecock:
- A shuttlecock consists of two main parts: the upper part which holds the feathers and the lower part which is typically rounded.
2. Identifying the Geometric Shapes:
- The upper part of the shuttlecock resembles a frustum of a cone because it has a wider top and a narrower bottom.
- The lower part of the shuttlecock is shaped like a hemisphere, which is a half of a sphere.
3. Combining the Shapes:
- Therefore, we can conclude that the shuttlecock is a combination of a frustum of a cone (for the feather part) and a hemisphere (for the rounded bottom part).
4. Evaluating the Options:
- Now, let's evaluate the given options:
- Option 1: Combination of a cylinder and a sphere - Incorrect
- Option 2: Combination of a cylinder and a hemisphere - Incorrect
- Option 3: Combination of a sphere and a cone - Incorrect
- Option 4: Combination of a frustum of a cone and a hemisphere - Correct
5. Final Conclusion:
- The correct answer is that a shuttlecock is a combination of a frustum of a cone and a hemisphere.
- A shuttlecock consists of two main parts: the upper part which holds the feathers and the lower part which is typically rounded.
- The upper part of the shuttlecock resembles a frustum of a cone because it has a wider top and a narrower bottom.
- The lower part of the shuttlecock is shaped like a hemisphere, which is a half of a sphere.
- Therefore, we can conclude that the shuttlecock is a combination of a frustum of a cone (for the feather part) and a hemisphere (for the rounded bottom part).
- Now, let's evaluate the given options:
- Option 1: Combination of a cylinder and a sphere - Incorrect
- Option 2: Combination of a cylinder and a hemisphere - Incorrect
- Option 3: Combination of a sphere and a cone - Incorrect
- Option 4: Combination of a frustum of a cone and a hemisphere - Correct
- The correct answer is that a shuttlecock is a combination of a frustum of a cone and a hemisphere.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS8videos
SURFACE AREAS AND VOLUMES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - SHORT ANSWER TYOE QUESTIONS14videos
SURFACE AREAS AND VOLUMES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ASWERS QUESTIONS14videos
STATISTICS AND PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Long Answer Type Questions18videos
TRIANGLES
Similar Questions
A shuttle cock used for playing badminton has the shape of a frustum of a cone mounted on a hemisphere. The diameters of the ends of the frustum are 5 cm and 2 cm; the height of the entire shuttle cock is 7 cm. Find the external surface area.
View SolutionA child playing with building blocks, which are of the shape of the cubes, has build a structure. If the edge of each cube is 3cm, find the volume of the structure built by the child.
View Solution
Knowledge Check
- Question 1 - Select One
What is the MA of the system of pulleys used in the below combination?
 A2 times the number of pulleysB2 number of movable pulleysC2/number of pulleysD2 + number of pulleys
A2 times the number of pulleysB2 number of movable pulleysC2/number of pulleysD2 + number of pulleys
Which of the following d-orbitals has donut shape ?
View SolutionWhich of the following compound has linear shape?
View Solution(A) : Repeaters are used to extend the range of communication
(R) : Repeater is combination of a receiver and a transmitter.View SolutionDiscuss the shape of the IF5 using VSEPR model .
View SolutionWhich of the following d-orbitals has dough-nut shape ?
View SolutionThe shape of a gilli in the gilli-danda game (see figure) is a combination of
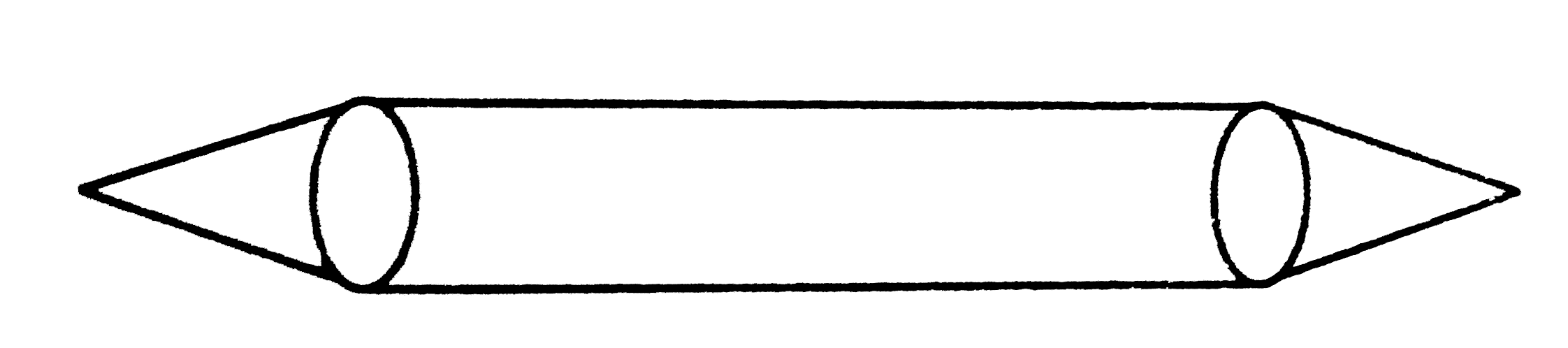 View Solution
View SolutionA child playing with building blocks, which are of the shape of cubes, has built a structure as shown in Fig. 13.25. If the edge of each cube is 3 cm, find the volume of the structure built by the child.
View Solution

