The standard deviation of some temperature data in .∘C is 5 .If the data were converted into .∘F then variance would be
81
57
36
25
The correct Answer is:A
To solve the problem, we need to find the variance of temperature data in Fahrenheit given that the standard deviation in Celsius is 5.
1. Understand the relationship between Celsius and Fahrenheit:
The formula to convert Celsius (C) to Fahrenheit (F) is:
F=95C+32
This formula consists of a multiplication factor (95) and a constant addition (32).
2. Identify the effect of constants on standard deviation:
When converting data using a linear transformation of the form kX+b, where k is a constant and b is a constant added to the data:
- The standard deviation is affected only by the multiplication factor k.
- The addition of a constant b does not affect the standard deviation.
3. Calculate the standard deviation in Fahrenheit:
Given that the standard deviation in Celsius is 5, we can find the standard deviation in Fahrenheit using the multiplication factor:
Standard deviation in Fahrenheit=95×Standard deviation in Celsius
Substituting the known value:
Standard deviation in Fahrenheit=95×5
Simplifying this gives:
Standard deviation in Fahrenheit=9
4. Calculate the variance in Fahrenheit:
Variance is the square of the standard deviation. Therefore, we can find the variance in Fahrenheit as follows:
Variance in Fahrenheit=(Standard deviation in Fahrenheit)2
Substituting the value we found:
Variance in Fahrenheit=92=81
Final Answer:
The variance of the temperature data in Fahrenheit is 81.
The formula to convert Celsius (C) to Fahrenheit (F) is:
F=95C+32
This formula consists of a multiplication factor (95) and a constant addition (32).
When converting data using a linear transformation of the form kX+b, where k is a constant and b is a constant added to the data:
- The standard deviation is affected only by the multiplication factor k.
- The addition of a constant b does not affect the standard deviation.
Given that the standard deviation in Celsius is 5, we can find the standard deviation in Fahrenheit using the multiplication factor:
Standard deviation in Fahrenheit=95×Standard deviation in Celsius
Substituting the known value:
Standard deviation in Fahrenheit=95×5
Simplifying this gives:
Standard deviation in Fahrenheit=9
Variance is the square of the standard deviation. Therefore, we can find the variance in Fahrenheit as follows:
Variance in Fahrenheit=(Standard deviation in Fahrenheit)2
Substituting the value we found:
Variance in Fahrenheit=92=81
The variance of the temperature data in Fahrenheit is 81.
Topper's Solved these Questions
- STATISTICSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICSEXERCISE - FILLERS
7 Videos
- STATISTICSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICSEXERCISE - LONG ANSWER TYPE QUESTIONS
8 Videos
- SETSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SETSEXERCISE - TRUE AND FALSE
6 Videos
- STRAIGHT LINESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - MATCHING THE COLUMN
3 Videos
Similar Questions
Mean deviation from mean of the data is

View SolutionFind the standard deviation for the following data

View SolutionFind the standard deviation for the following data

View SolutionFind the standard deviation from the following data:

View SolutionFind the standard deviation from the following datas:
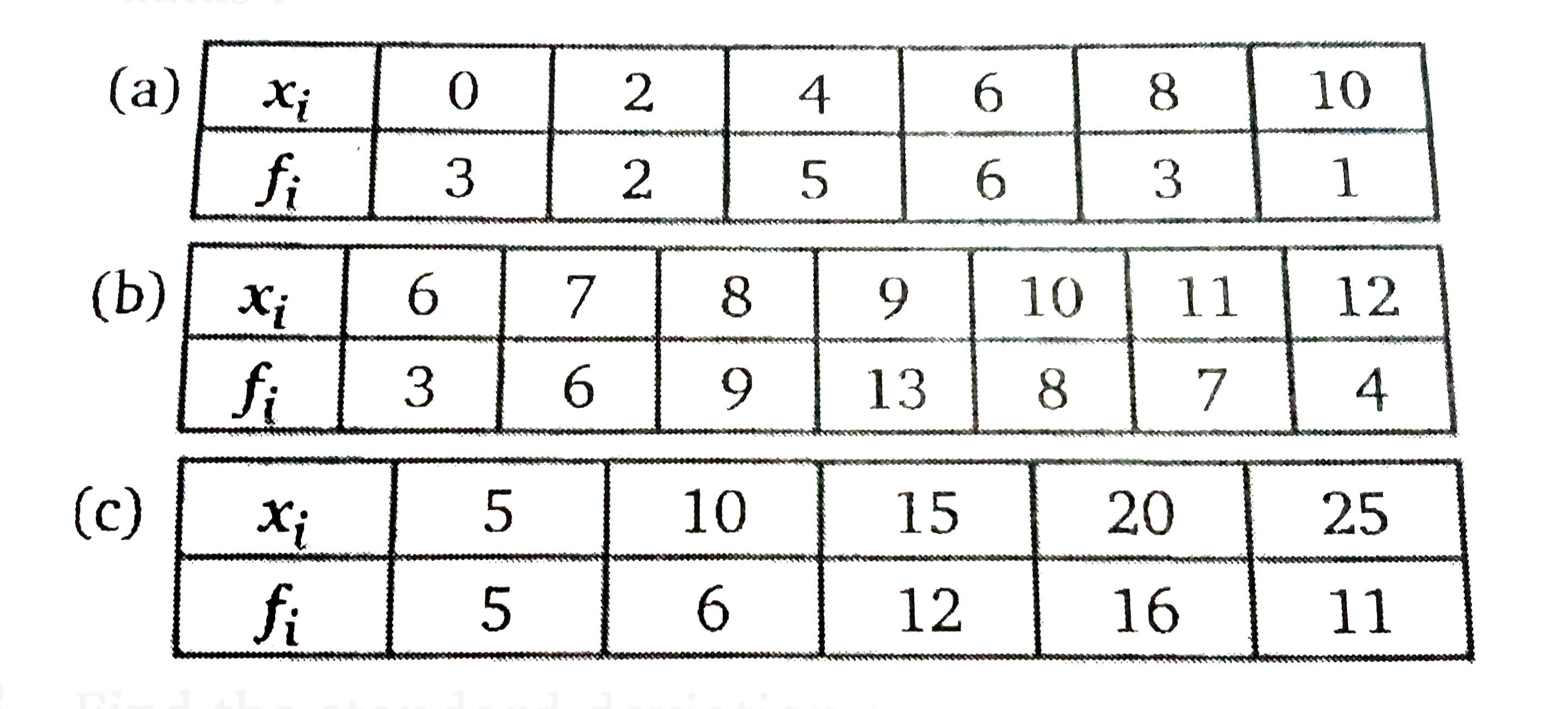
View SolutionThe standard deviation of data 6,5,9,13,12,8 and 10 is
View SolutionThe standard deviation of data 6,5,9,13,12,8 and 10 is
View SolutionThe standard deviation of data 6,5,9,13,12,8 and 10 is
View SolutionThe mean deviation from mean of the data 90,100,125,115,110 is
View SolutionFind the standard deviation from the following datas, using assumed mean:
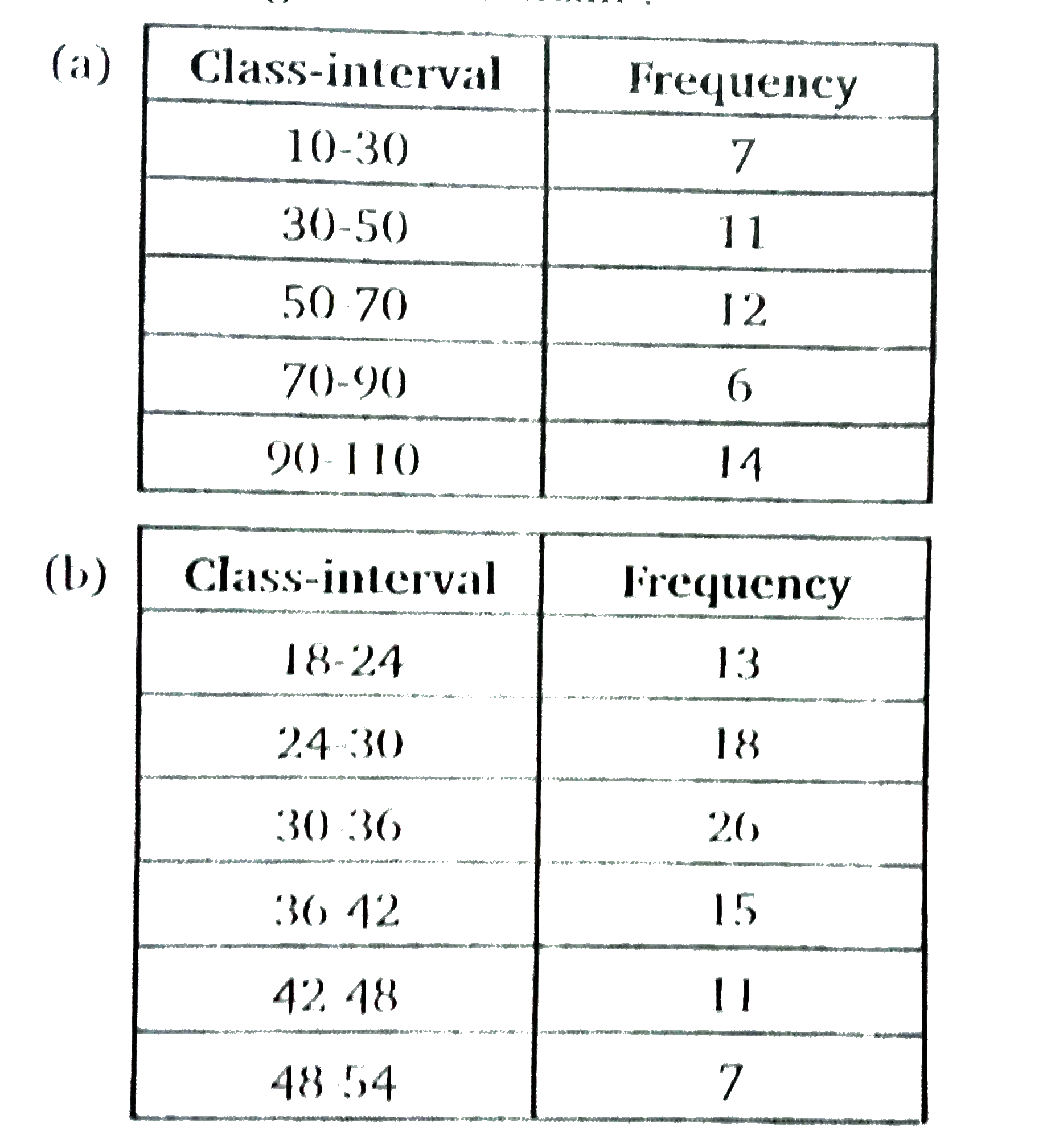
View Solution