Following are the marks obtained by 9 student in a mathematics test
50,69,20,33,53,39,40,65,59,
The mean deviation from the median is
9
10.5
12.67
14.76
The correct Answer is:C
To solve the problem of finding the mean deviation from the median for the given marks, we will follow these steps:
Step 1: Arrange the Data in Ascending Order
The marks obtained by the students are:
50, 69, 20, 33, 53, 39, 40, 65, 59.
Arranging these in ascending order:
20, 33, 39, 40, 50, 53, 59, 65, 69.
Step 2: Calculate the Median
To find the median, we need to identify the middle value in the ordered list. Since there are 9 observations (an odd number), the median is the value at the position (n+1)/2, where n is the number of observations.
Median position=9+12=5
The 5th value in the ordered list is 50. Therefore, the median is:
Median=50
Step 3: Calculate the Deviations from the Median
Next, we calculate the absolute deviations from the median (50) for each mark:
- For 20: |20−50|=30
- For 33: |33−50|=17
- For 39: |39−50|=11
- For 40: |40−50|=10
- For 50: |50−50|=0
- For 53: |53−50|=3
- For 59: |59−50|=9
- For 65: |65−50|=15
- For 69: |69−50|=19
The deviations are:
30, 17, 11, 10, 0, 3, 9, 15, 19.
Step 4: Calculate the Mean Deviation
Now, we sum up all the absolute deviations and divide by the number of observations (9):
Sum of deviations=30+17+11+10+0+3+9+15+19=114
Now, we calculate the mean deviation:
Mean Deviation=Sum of deviationsn=1149≈12.67
Final Answer
The mean deviation from the median is approximately:
Mean Deviation≈12.67
---
The marks obtained by the students are:
50, 69, 20, 33, 53, 39, 40, 65, 59.
20, 33, 39, 40, 50, 53, 59, 65, 69.
To find the median, we need to identify the middle value in the ordered list. Since there are 9 observations (an odd number), the median is the value at the position (n+1)/2, where n is the number of observations.
Median=50
Next, we calculate the absolute deviations from the median (50) for each mark:
- For 33: |33−50|=17
- For 39: |39−50|=11
- For 40: |40−50|=10
- For 50: |50−50|=0
- For 53: |53−50|=3
- For 59: |59−50|=9
- For 65: |65−50|=15
- For 69: |69−50|=19
30, 17, 11, 10, 0, 3, 9, 15, 19.
Now, we sum up all the absolute deviations and divide by the number of observations (9):
Mean Deviation=Sum of deviationsn=1149≈12.67
The mean deviation from the median is approximately:
Mean Deviation≈12.67
Topper's Solved these Questions
- STATISTICSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICSEXERCISE - FILLERS
7 Videos
- STATISTICSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICSEXERCISE - LONG ANSWER TYPE QUESTIONS
8 Videos
- SETSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SETSEXERCISE - TRUE AND FALSE
6 Videos
- STRAIGHT LINESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - MATCHING THE COLUMN
3 Videos
Similar Questions
Following are the marks obtained by 30 students in a examination

Taking class intervals 0−10,10−20,…..40−50 construct a frequency table.
View SolutionFollowing table shows the marks obtained by 8 students in English and Mathematics.

A candidate scored 85 marks in Y but was absent from the X test. Estimate his probable score for other test.
View SolutionFind the mean, median and mode of the following marks obtained by 16 students in a class test marked out of 10 marks:
0,0,2,2,3,3,3,4,5,5,5,5,6,6,7 and 8
View SolutionThe marks of 9 students in a test were 13,17,20,3,5,3,20,15 and 18. Find quartile deviation.
View SolutionFollowing is the distribution fo marks obtained by 50 students in a test.
Marks more than01020304050No. of Students50464020103
If 60% of the students pass the test, find the minimum marks obtained by a pass students.
View SolutionFollowing table shows the marks scored by a group of 90 students in a mathematics test of 100 marks. Marks 0-20 20-30 30-40 40-50 50-60 60-70 70-100 No. of Students: 7 10 10 20 20 15 8 Find the probability that marks scored by a student in the class is: at most 60 marks (ii) at least 60 marks (iii)not more than 50 marks
View SolutionThe marks (out of 100) obtained by a group of students in a science test are 85, 76,90, 85, 39, 48, 56, 95, 81 and 75. Find the:(i) Highest and the lowest marks obtained by the students.(ii) Range of the marks obtained.(iii) Mean marks obtained by the group.
View SolutionThe marks (out of 100) obtained by a group of students in a science test are 85, 76, 90, 85, 39, 48, 56, 95, 81 and 75. Find the: (i) Highest and the lowest marks obtained by the students. (ii) Range of the marks obtained. (iii) Mean marks obtain
View SolutionThe marks obtained by 100 students in a Mathematics test are given below :

Draw an ogive for the given distribution on a graph sheet.
(Use a scale of 2 cm = 10 units on both axis).
Use the ogive to estimate the :
(i) median.
View SolutionThe marks obtained by 120 students in a Mathematics test are given below:
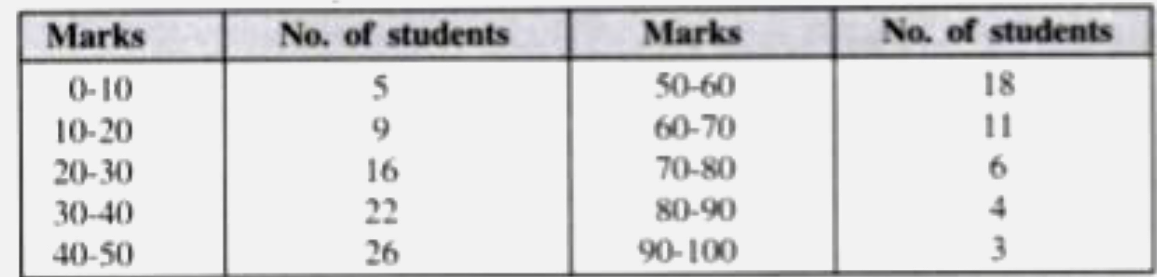
Using the informations, given above, draw an ogive on a graph sheet. Take a suitable scale for your ogive. Use the ogive drawn to estimate :
(i) the median.
(ii) the number of students who obtained more than 75% marks in the test.
(iii) the number of students who did not pass in the test if the pass percentage was 40.
View Solution
