If the sum of the areas of two circles with radii R1 and R2 is equal to the area of a circle of radius R, then
R1+R2=R
R21+R22=R2
R1+R2<R
R21+R22<R2
The correct Answer is:B
To solve the problem, we need to establish the relationship between the areas of the circles based on the given information.
1. Understand the Area of a Circle:
The area A of a circle is given by the formula:
A=πr2
where r is the radius of the circle.
2. Write the Areas of the Given Circles:
For the two circles with radii R1 and R2, the areas can be expressed as:
Area of Circle 1=πR21
Area of Circle 2=πR22
3. Sum the Areas of the Two Circles:
The sum of the areas of the two circles is:
Total Area=πR21+πR22
4. Area of the Circle with Radius R:
The area of the circle with radius R is:
Area of Circle with radius R=πR2
5. Set Up the Equation:
According to the problem, the sum of the areas of the two circles is equal to the area of the circle with radius R:
πR21+πR22=πR2
6. Factor Out π:
We can factor π from the left-hand side:
π(R21+R22)=πR2
7. Cancel π:
Since π is common on both sides, we can cancel it out (assuming π≠0):
R21+R22=R2
8. Conclusion:
Thus, we have established that:
R2=R21+R22
Final Result:
The relationship between the radii is given by:
R2=R21+R22
The area A of a circle is given by the formula:
A=πr2
where r is the radius of the circle.
For the two circles with radii R1 and R2, the areas can be expressed as:
Area of Circle 1=πR21
Area of Circle 2=πR22
The sum of the areas of the two circles is:
Total Area=πR21+πR22
The area of the circle with radius R is:
Area of Circle with radius R=πR2
According to the problem, the sum of the areas of the two circles is equal to the area of the circle with radius R:
πR21+πR22=πR2
We can factor π from the left-hand side:
π(R21+R22)=πR2
Since π is common on both sides, we can cancel it out (assuming π≠0):
R21+R22=R2
Thus, we have established that:
R2=R21+R22
The relationship between the radii is given by:
R2=R21+R22
Topper's Solved these Questions
- AREAS RELATED TO CIRCLEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - AREAS RELATED TO CIRCLEEXERCISE - Very Short Answer Questions
14 Videos
- AREAS RELATED TO CIRCLEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - AREAS RELATED TO CIRCLEEXERCISE - Short Answer Type Questions
16 Videos
- ARITHMETIC PROGRESSIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Long Answer Type Questions
10 Videos
Similar Questions
If the sum of the circumferences of two circles with radii R1 and R2 is equal to the circumference of a circle of radius R, then
View SolutionIf the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding of the other circle. Is this statement false ? Why ?
View Solution
Knowledge Check
What is the area of the circle whose radius is the average of the radii of two circles with areas of 16πand100π?
A25πB36πC49πD64π
The diameters of two given circles are in the ratio 3:4 and the sum of the areas of the circles is equal to the area of a circle whose diameter measures 30m. Find the diameter of the given circles.
View SolutionIf O is the centre of a circle with radius r and AB is a chord of the circle at a distance r2 from O, then ∠BAO=
View SolutionThe diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm is
View SolutionThe radii of two circles are in the ratio 2:5. What is the ratio of their areas ?
View SolutionAs show in the figure , the five circles are tangent to one another consecutively and to the lines L1andL2. If the radius of the largest circle is 18 and that of the smaller one is 8, if radius of the middle circle is r, then find the value of r/2.
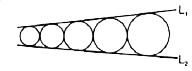
View SolutionLet ABC be an isosceles triangle with base BC. If r is the radius of the circle inscribsed in ΔABCandr1 is the radius of the circle ecribed opposite to the angle A, then the product r1r can be equal to (where R is the radius of the circumcircle of ΔABC)
View SolutionIf the ratio of the radii of two circles is 2:3, find the ratio of their areas.
View Solution