If O is the centre of a circle with radius r and AB is a chord of the circle at a distance r2 from O, then ∠BAO=
To solve the problem, we need to find the angle ∠BAO given that O is the center of a circle with radius r, and the chord AB is at a distance r2 from the center O.
1. Draw the Circle and Identify Points:
- Draw a circle with center O and radius r.
- Mark a chord AB such that the perpendicular distance from O to AB is r2. Let the foot of the perpendicular from O to AB be point D.
2. Label the Distances:
- Since O is the center of the circle, OA=OB=r (the radius).
- The distance OD=r2 (given).
3. Identify the Right Triangle:
- In triangle OAD, we have:
- OA=r (hypotenuse),
- OD=r2 (one leg),
- AD is the other leg which we need to find.
4. Use Pythagoras' Theorem:
- According to the Pythagorean theorem:
OA2=OD2+AD2
- Substituting the known values:
r2=(r2)2+AD2
- This simplifies to:
r2=r24+AD2
- Rearranging gives:
AD2=r2−r24=3r24
- Taking the square root:
AD=r√32
5. Consider Triangle AOD:
- Now we have triangle AOD where:
- OA=r,
- OD=r2,
- AD=r√32.
- We can find ∠AOD using the sine function:
sin(∠AOD)=ADOA=r√32r=√32
- Therefore, ∠AOD=60∘.
6. Find Angle ∠BAO:
- Since AD is the perpendicular bisector of chord AB, it bisects ∠AOB.
- Thus, ∠AOB=2×∠BAO.
- Therefore, ∠BAO=12×60∘=30∘.
Final Answer:
∠BAO=30∘
- Draw a circle with center O and radius r.
- Mark a chord AB such that the perpendicular distance from O to AB is r2. Let the foot of the perpendicular from O to AB be point D.
- Since O is the center of the circle, OA=OB=r (the radius).
- The distance OD=r2 (given).
- In triangle OAD, we have:
- OA=r (hypotenuse),
- OD=r2 (one leg),
- AD is the other leg which we need to find.
- According to the Pythagorean theorem:
OA2=OD2+AD2
- Substituting the known values:
r2=(r2)2+AD2
- This simplifies to:
r2=r24+AD2
- Rearranging gives:
AD2=r2−r24=3r24
- Taking the square root:
AD=r√32
- Now we have triangle AOD where:
- OA=r,
- OD=r2,
- AD=r√32.
- We can find ∠AOD using the sine function:
sin(∠AOD)=ADOA=r√32r=√32
- Therefore, ∠AOD=60∘.
- Since AD is the perpendicular bisector of chord AB, it bisects ∠AOB.
- Thus, ∠AOB=2×∠BAO.
- Therefore, ∠BAO=12×60∘=30∘.
∠BAO=30∘
Topper's Solved these Questions
Similar Questions
Construct a circle with centre O and radius 4 cm.
View SolutionIn the adjoining figure, O is the centre of the circle. If the chord AB is equal to the radius of the circle, then find the value of ∠ADB.

View Solution(i) Find the length of a chord which is at a distance of 12 cm from the centre of a circle of radius 13cm.
(ii) The length of a chord is 16 cm of a circle of diameter 2 cm. find the perpendicular distance of this chord from the centre of the circle.
View SolutionPQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR=120o , then ∠OPQ is 60o (b) 45o (c) 30o (d) 90o
View SolutionO is the centre of a circle of diameter AB. If chord AC= chord BC, then find the value of ∠ABC.
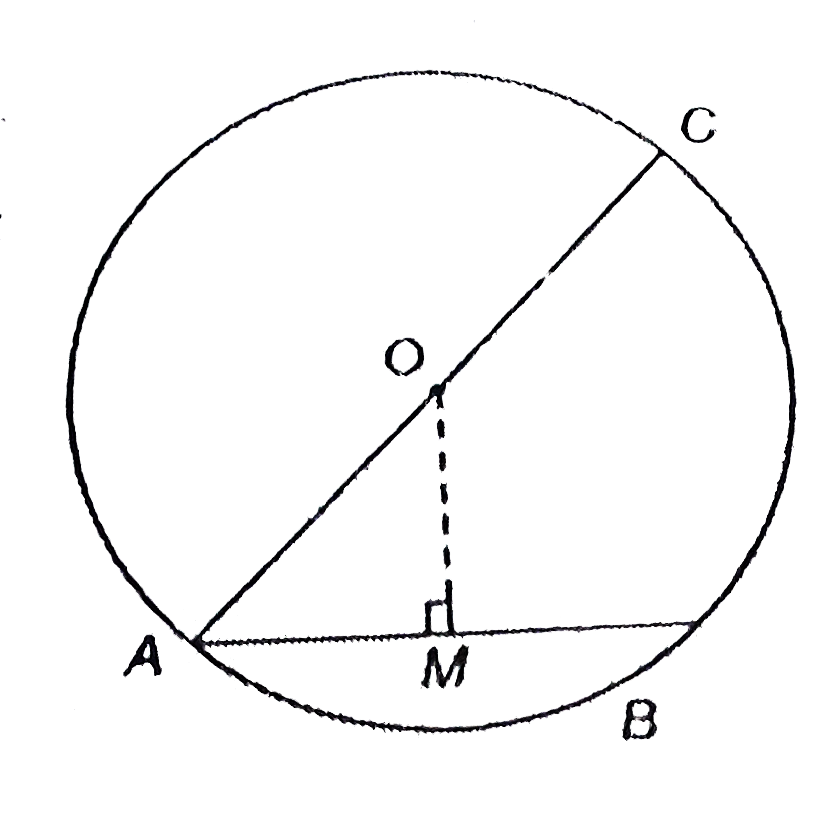
View SolutionIn the adjoining figure, O is the centre of the centre of the circle. If diameter AC=26cm and chord AB=10cm, then find the distances of the chord AB from the centre of the circle.
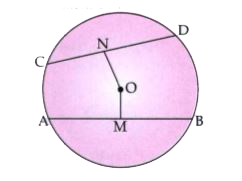
View SolutionIn the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the :
(i) radius of the circle
(ii) length of chord CD
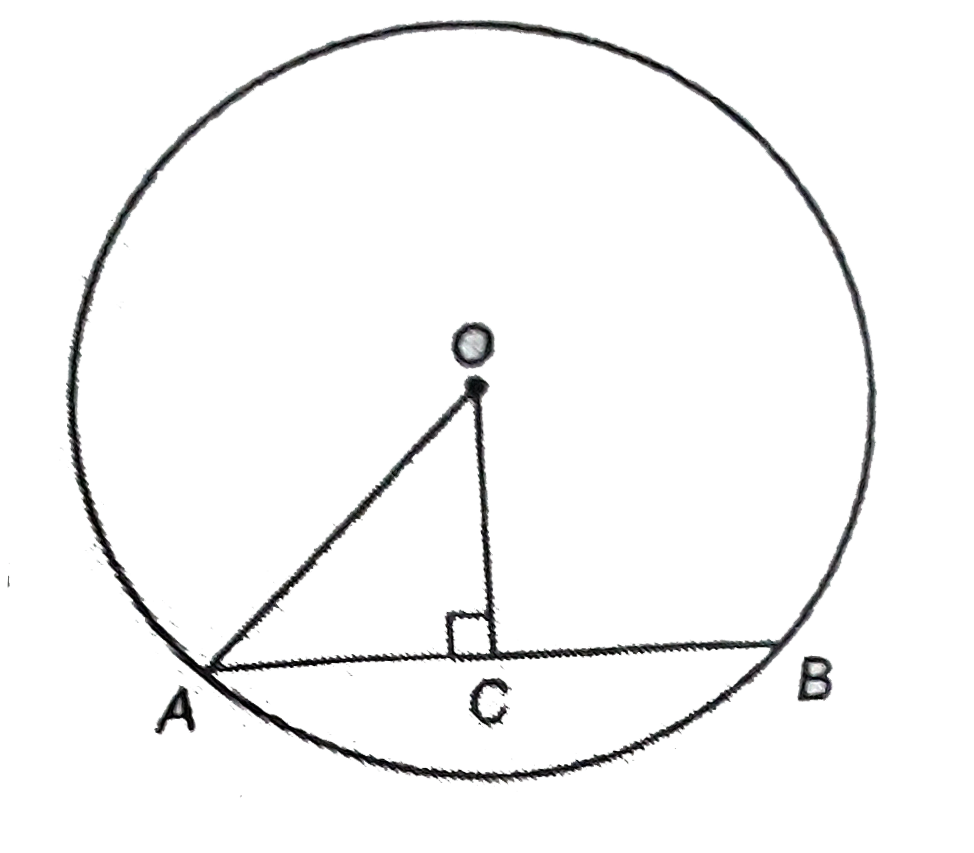
View SolutionIn the adjoining figure O is the centre of circle and c is the mid point. the radius of circle is 17 cm . if OC=8cm, then find the length of chord AB.
View SolutionTwo chords AB and CD of a circle are each at distances 4 cm from the centre. Then,
View SolutionIf a chord AB subtends and angle of 60∘ at the centre of a circle, then the angle between the tangents to the circle drawn from A and B is
View Solution