The probability distribution of a random variable X is given below
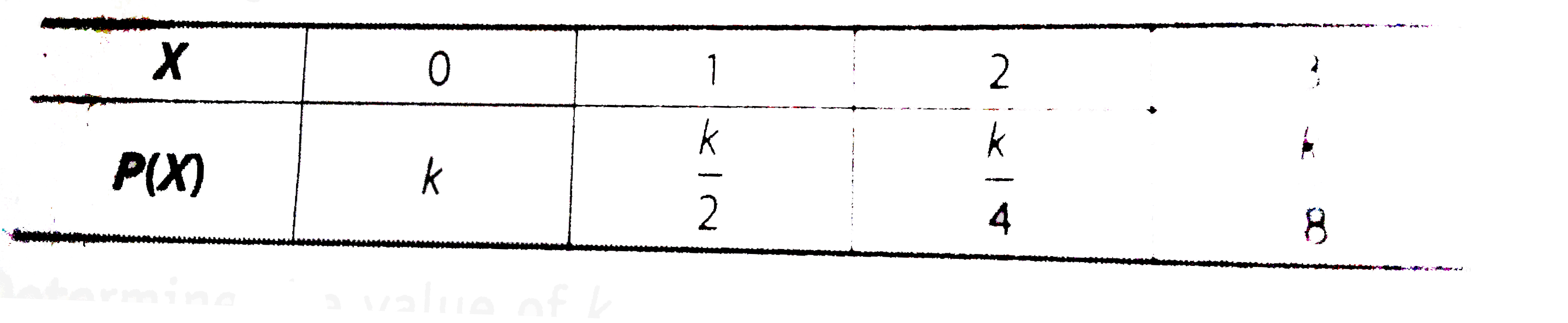
(i) Determine the value of K .
(ii) Determine P(X≤2)andP(X>2).
(iii) Find P(X≤2)+P(X>2).
We have,
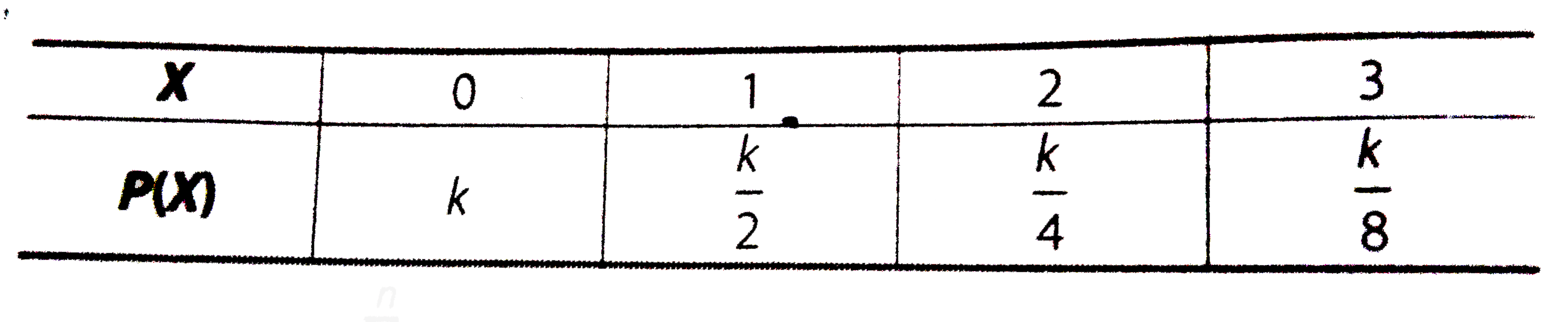
(i) Since, n∑i=1Pi=1,i=1,2,…..,nandPi≥0
∴k+k2+k4+k8=1
⇒8k+4k+2k+k=8
∴k=815
(ii) P(X≤2)=P(0)+P(1)+P(2)=k+k2+k4
=(4k+2k+k)4=7k4=74⋅815=1415
and P(X>2)=P(3)=k8=18⋅815=115
(iii) P(X≤2)+P(X≥2)=1415+115=1
Topper's Solved these Questions
- PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - Long Answer Type Questions
15 Videos
- PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - Objective Type Questions
38 Videos
- MATRICESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MATRICESEXERCISE - Solved example
101 Videos
- RELATIONS AND FUNCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Fillers
15 Videos
Similar Questions
The probability of a random variable X is given below
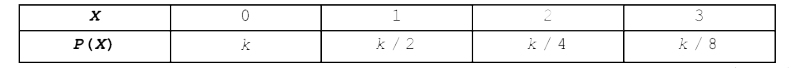
Determine the value of k
View SolutionThe probability distribution of a discreate random variable X is given below :

The value of k is
View SolutionThe probability distribution of a random variable X is given below.

Find k, mean and variance of X
View SolutionThe probability distribution of a discrete random variable X is given below

The value of k is
View SolutionThe probability of a random variable X is given below

Determine P(X≤2) and P(X>2)
View SolutionThe probability distribution of a random variable X is given as under:

Find k , and P (X<6) .
View SolutionThe probability of a random variable X is given below
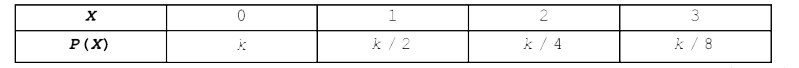
Find P(X≤2)+P(X>2)
View SolutionFind the value of k for probability distribution of a random variable X is give by:

View SolutionThe probability distribution of a random variable X is given below: X: 0 1 2 3 P(X):k k2 k4 k8 (i) Determine the value of k (ii) Determine P(X≤2)and P(X>2) (iii) Find P(X≤2)+P(X>2)
View SolutionConsider the probability distribution of a random variable X

Calculate
(i) V(X2) (ii) Variance of X.
View Solution
