The probability distribution of a random variable X is given below: X: 0 1 2 3 P(X):k k2 k4 k8 (i) Determine the value of k (ii) Determine P(X≤2)and P(X>2) (iii) Find P(X≤2)+P(X>2)
Let's solve the problem step by step.
Given:
The probability distribution of a random variable X is as follows:
- X:0,1,2,3
- P(X):k,k2,k4,k8
(i) Determine the value of k
To find the value of k, we use the fact that the sum of all probabilities must equal 1.
P(X=0)+P(X=1)+P(X=2)+P(X=3)=1
Substituting the probabilities:
k+k2+k4+k8=1
To combine these terms, we need a common denominator. The least common multiple of 1, 2, 4, and 8 is 8. Rewriting each term:
8k8+4k8+2k8+k8=1
Now, combine the fractions:
8k+4k+2k+k8=1
This simplifies to:
15k8=1
Now, solve for k:
15k=8⟹k=815
(ii) Determine P(X≤2) and P(X>2)
To find P(X≤2):
This includes the probabilities for X=0, X=1, and X=2:
P(X≤2)=P(X=0)+P(X=1)+P(X=2)
Substituting the values of k:
P(X=0)=k=815
P(X=1)=k2=8/152=415
P(X=2)=k4=8/154=215
Now, add these probabilities:
P(X≤2)=815+415+215=1415
To find P(X>2):
This includes the probability for X=3:
P(X>2)=P(X=3)=k8=8/158=115
(iii) Find P(X≤2)+P(X>2)
Now we can find the sum:
P(X≤2)+P(X>2)=1415+115=1515=1
Final Answers:
1. k=815
2. P(X≤2)=1415 and P(X>2)=115
3. P(X≤2)+P(X>2)=1
The probability distribution of a random variable X is as follows:
- X:0,1,2,3
- P(X):k,k2,k4,k8
P(X=1)=k2=8/152=415
P(X=2)=k4=8/154=215
1. k=815
2. P(X≤2)=1415 and P(X>2)=115
3. P(X≤2)+P(X>2)=1
Topper's Solved these Questions
Similar Questions
The probability distribution of a random variable X is given below: X: 0 1 2 3 P(X):k k2 k4 k8 (i) Determine the value of k (ii) Determine P(X≤2)and P(X>2) (iii) Find P(X≤2)+P(X>2)
View SolutionIf the probability distribution of a random variable X is given by X=xi: 1 2 3 4 P(X=xi): 2k 4k 3k k Write the value of k .
View SolutionThe probability distribution of a discrete random variable X is given below

The value of k is
View SolutionThe probability distribution of a discreate random variable X is given below :

The value of k is
View SolutionThe probability distribution of a random variable X is given below.

Find k, mean and variance of X
View SolutionThe probability distribution of a discrete random variable X is given below: X: 2 3 4 5 P(X):5k 7k 9k 11k The value of E(X) is
View SolutionThe probability distribution of a random variable X is given as under:

Find k , and P (X<6) .
View SolutionFind the value of k for probability distribution of a random variable X is give by:

View SolutionThe probability of a random variable X is given below
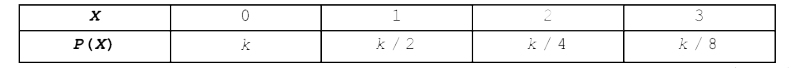
Determine the value of k
View SolutionIf the probability distribution of a random variable X is as given below: X=xi: 1 2 3 4 P(X=xi): c 2c 3c 4c Write the value of P(X≤2) .
View Solution
