Using integration, find the area bounded by the curve $x^{2} = 4 y$ and the line $x = 4 y - 2 .$

A

$\frac{3}{8} sq units$

B

$\frac{5}{8} sq unit$

C

$\frac{7}{8} sq unit$

D

$\frac{9}{8} sq units$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Given equation of curve is $x^{2} 4 y and the straight line x = 4 y - 2$

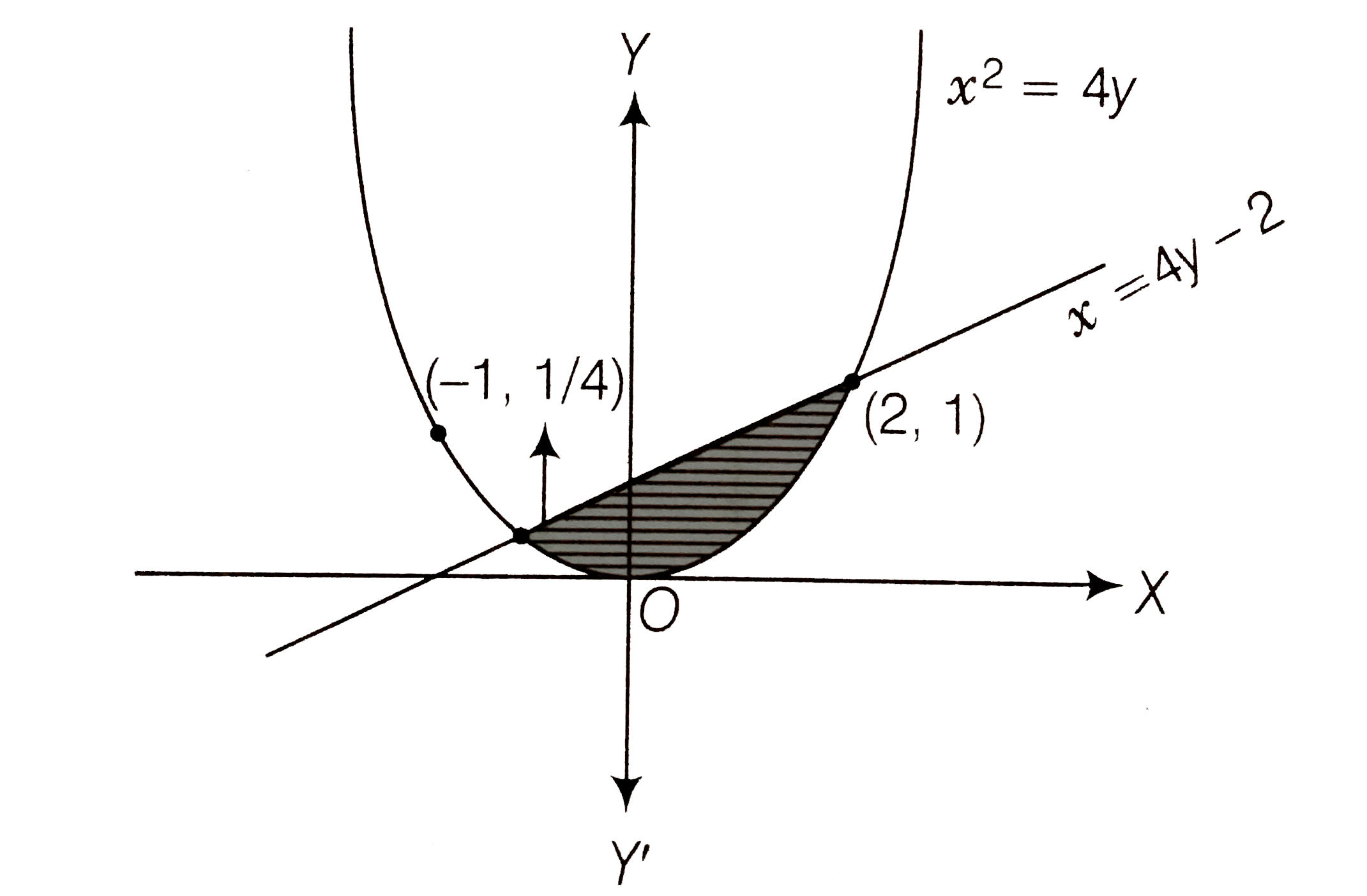
For intresection point, put $x = 4 y - 2$ in equation of curve, we get
${(4 y - 2)}^{2} = 4 y$
$\Rightarrow 16 y^{2} + 4 - 16 y = 4 y$
$\Rightarrow 16 y^{2} - 20 y + 4 = 0$
$\Rightarrow 4 y^{2} - 5 y + 1 = 0$
$\Rightarrow 4 y (y - 1) - 1 (y - 1) = 0$
$\Rightarrow (4 y - 1) (y - 1) = 0$
$∴ y = 1, \frac{1}{4}$
For $y = 1, x = \sqrt{4.1} = 2$ [since, negative value does not satisfy the equation of line]
For $y = \frac{1}{4}, x = \sqrt{4} . \frac{1}{4} = - 1$ [positive value does not satisfy the equation of line]
So, the intersection points are (2, 1) and $(- 1, \frac{1}{4})$
$∴ Area of shaded region = \int_{- 1}^{2} (\frac{x + 2}{4}) d x - \int_{- 1}^{2} \frac{x^{2}}{4} d x$
$= \frac{1}{4} {[\frac{x^{2}}{2} + 2 x]}_{- 1}^{2} - \frac{1}{4} {∣ ∣ ∣ \frac{x^{3}}{3} ∣ ∣ ∣}_{- 1}^{2}$
$= - \frac{1}{4} [\frac{4}{2} + 4 - - \frac{1}{2} + 2] - \frac{1}{4} [\frac{8}{3} + \frac{1}{3}]$
$= \frac{1}{4} . \frac{15}{2} - \frac{1}{4} . \frac{9}{3} = \frac{45 - 18}{24}$
$= \frac{27}{24} = \frac{9}{8} sq units$

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

NCERT EXEMPLAR ENGLISH-APPLICATION OF INTEGRALS-Objective Type Questions

Home
Ask Doubt
Profile