The area of the region bounded by parabola $y^{2} = x$ and the straight line $2 y = x$ is

A

$\frac{4}{3} sq units$

B

$1 sq unit$

C

$\frac{2}{3} sq unit$

D

$\frac{1}{3} sq units$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

We have to find the area enclosed by parabola $y^{2} = x$ and the straight line $2 y = x$ .

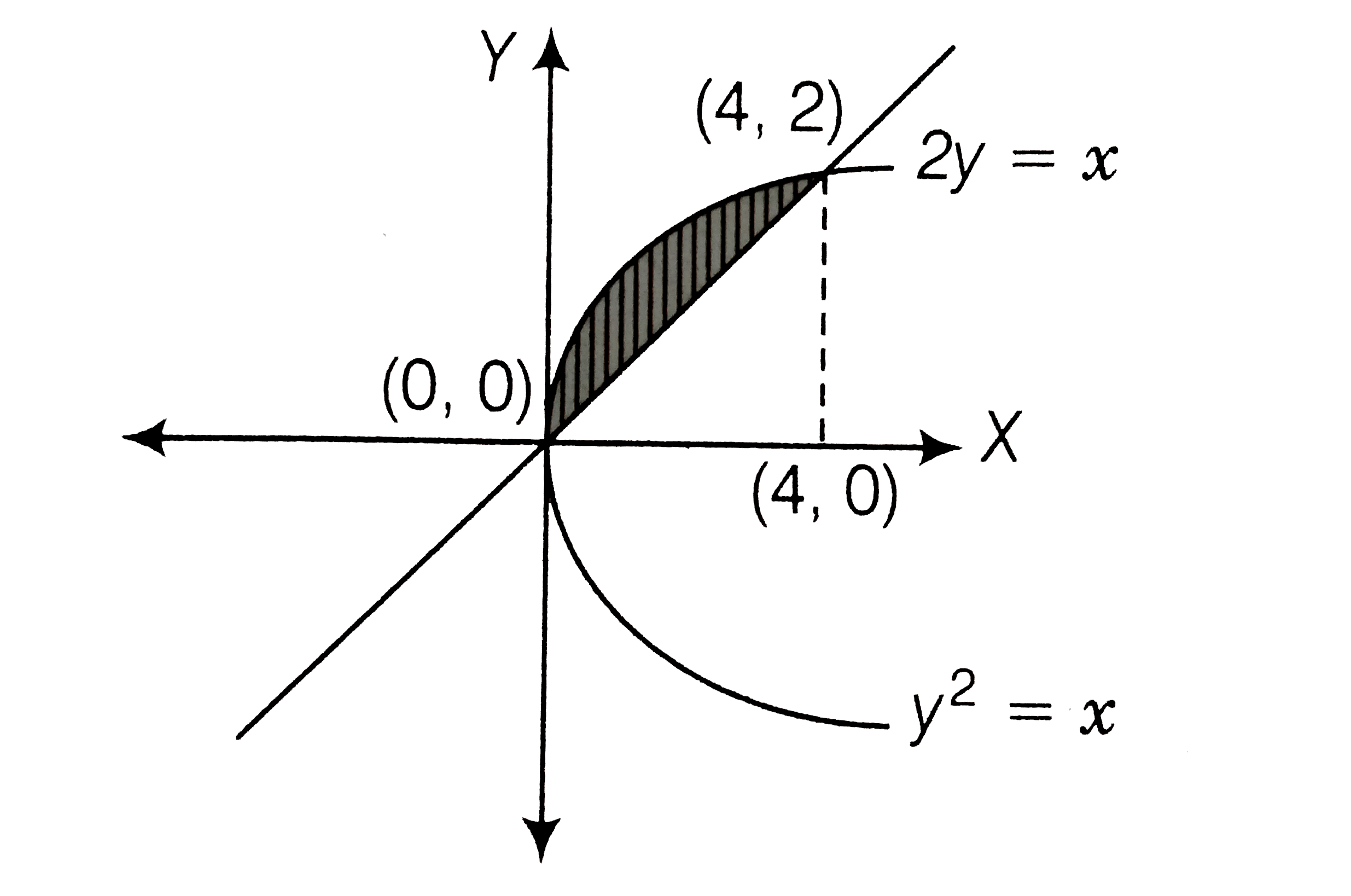
$∴ {(x - 2)}^{2} = x$
$\Rightarrow x^{2} = 4 x \Rightarrow x (x - 4) = 0$
$\Rightarrow x = 4 \Rightarrow y = 2 and x = 0 \Rightarrow y = 0$
So, the intersection points are (0,0) and (4,2).
Area enclosed by shaded region,
$A = \int_{0}^{4} [\sqrt{x} - \frac{x}{2}] d x$
$= {⎡ ⎣ \frac{c^{\frac{1}{2} + 1}}{\frac{1}{2} + 1} - \frac{1}{2} . \frac{x^{2}}{2} ⎤ ⎦}_{0}^{4} = {[2 . \frac{x^{3 / 2}}{3} - \frac{x^{2}}{4}]}_{0}^{4}$
$= \frac{2}{3} 4^{3 / 2} - \frac{16}{4} - \frac{2}{3} .0 + \frac{1}{4} .0$
$= \frac{16}{3} - \frac{16}{4} = \frac{64 - 48}{12} = \frac{16}{12} = \frac{4}{3} sq units$

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

NCERT EXEMPLAR ENGLISH-APPLICATION OF INTEGRALS-Objective Type Questions

Home
Ask Doubt
Profile