Can the potential function have a maximum or minimum is free space ?
To determine whether the potential function can have a maximum or minimum in free space, we can analyze the properties of electric potential and the conditions in free space.
1. Understanding Electric Potential:
The electric potential (V) at a point in space is defined as the work done per unit charge in bringing a positive test charge from infinity to that point.
2. Free Space Definition:
Free space, often referred to as a vacuum, is a region devoid of matter and atmospheric influences. This means there are no charges or fields from surrounding materials that could affect the potential.
3. Behavior of Electric Fields:
In free space, electric fields (E) can be described by the relationship E=−∇V, where ∇V is the gradient of the potential. If the potential function had a maximum or minimum, it would imply that the electric field is zero at that point (as the gradient would be zero).
4. Implication of Zero Electric Field:
If the electric field is zero, it indicates that there are no forces acting on a charge placed at that point. In free space, charges would not remain stationary at a point of maximum or minimum potential because there are no other charges to create a stable equilibrium.
5. Conclusion:
Since in free space there are no surrounding charges to create a stable point of maximum or minimum potential, the potential function cannot have a maximum or minimum value. The potential can vary continuously but does not settle at a maximum or minimum.
Final Answer:
No, the potential function cannot have a maximum or minimum value in free space.
---
The electric potential (V) at a point in space is defined as the work done per unit charge in bringing a positive test charge from infinity to that point.
Free space, often referred to as a vacuum, is a region devoid of matter and atmospheric influences. This means there are no charges or fields from surrounding materials that could affect the potential.
In free space, electric fields (E) can be described by the relationship E=−∇V, where ∇V is the gradient of the potential. If the potential function had a maximum or minimum, it would imply that the electric field is zero at that point (as the gradient would be zero).
If the electric field is zero, it indicates that there are no forces acting on a charge placed at that point. In free space, charges would not remain stationary at a point of maximum or minimum potential because there are no other charges to create a stable equilibrium.
Since in free space there are no surrounding charges to create a stable point of maximum or minimum potential, the potential function cannot have a maximum or minimum value. The potential can vary continuously but does not settle at a maximum or minimum.
No, the potential function cannot have a maximum or minimum value in free space.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Short Answer Type Question
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Long Answer Type Question
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - MCQ s (More than one Options)
7 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - LONG ANSWER
5 Videos
- MAGNETISM AND MATTER BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - All Questions
24 Videos
Similar Questions
Knowledge Check
The potential energy of a spring is the minimum when it is
AcompressedBextendedCat its natural lengthDat its natural length but is kept at a height above the ground
The material having minimum work function is
View SolutionIn the following graph, state the absolute and local maximum and minimum values of the function.
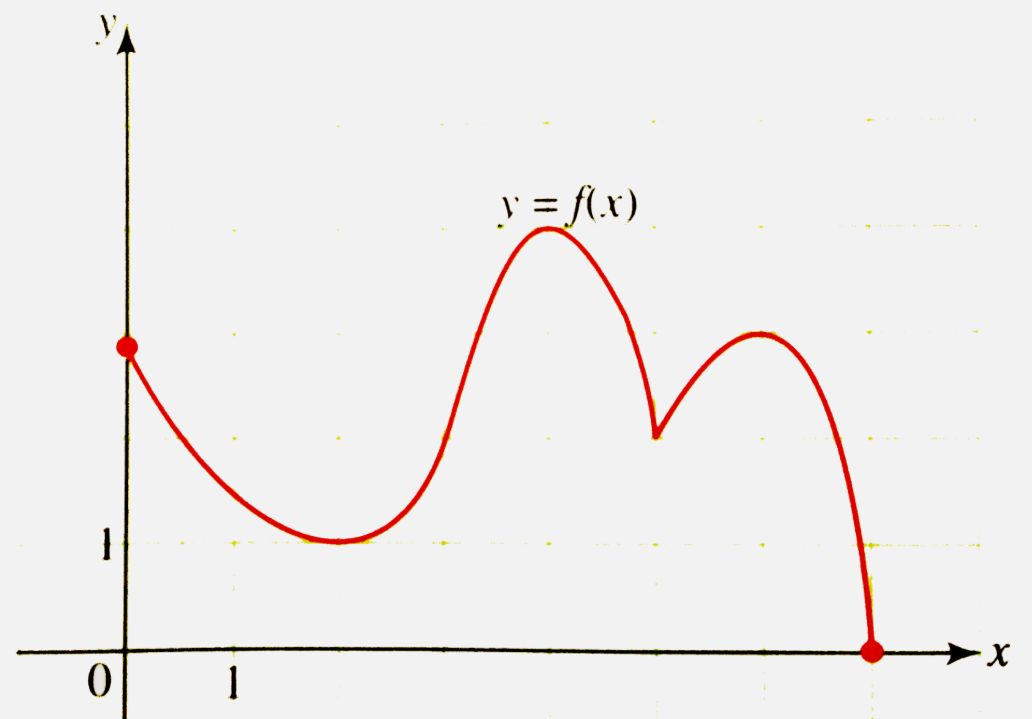
View SolutionIf x lies in first quadrant, find the maximum and minimum values of the function 4sinx+3cosx.
View SolutionThe absolute maximum and minimum values of functions can be found by their monotonic and asymptotic behaviour provided they exist. We may agree that finite limits values may be reagarded as absolute maximum or minimum. For instance the absolute maximum value of 11+x2 is unity. It is attained at x=0 while absolute maximum value of the same functions is zero which is a limiting value of (x→∞orx→−∞)
The function x4−4x+1 will have.
View SolutionFind the points of maximum ( local maximum ) and minimum ( local minimum ) of the function f(x)=x3−3x2−9x ?
View SolutionThe absolute maximum and minimum values of functions can be found by their monotonic and asymptotic behaviour provided they exist. We may agree that finite limits values may be reagarded as absolute maximum or minimum. For instance the absolute maximum value of 11+x2 is unity. It is attained at x=0 while absolute maximum value of the same functions is zero which is a limiting value of (x→∞orx→−∞)
The absolute minimum value of the function x−2√x2+1 is
View SolutionFor what values of x, the function f(x)=x5−5x4+5x3−1 is maximum or minimum? Prove that at x = 0, the function is neither maximum nor minimum.
View Solution
