A factory owner purchases two types of machines, A and B for his factory. The requirements and the limitations for the machines are as follows: \begin{vmatrix} Machine& Area\ occupied & Labour force & Daily \ output(in \ units)\\ A& 1000 \ m^{2} & 12 \ men & 60\\ B& 1200 \ m^{2} & 8\ men & 40 \end{vmatrix} He has maximum area of 9000 m2 available, and 72 skilled labourers who can operate both the machines. How many machines of each type should he buy to maximise the daily output?
Step by step video & image solution for A factory owner purchases two types of machines, A and B for his factory. The requirements and the limitations for the machines are as follows: \begin{vmatrix} Machine& Area\ occupied & Labour force & Daily \ output(in \ units)\\ A& 1000 \ m^{2} & 12 \ men & 60\\ B& 1200 \ m^{2} & 8\ men & 40 \end{vmatrix} He has maximum area of 9000\ m^2 available, and 72 skilled labourers who can operate both the machines. How many machines of each type should he buy to maximise the daily output? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A factory owner purchases two types of machines, A and B, for his factory. The requirements and limitations for the machines are as follows:

He has an area of 7600 sq. m available and 72 skilled men who can operate the machines. To find how many machines of each type should he buy to maximize the daily output, formulate this as a L.P.P.
View SolutionA mill owner buys two types of machines A and B for his mill, Machines A occupies 1,000 sq.m of area and requires 12 men to operate it, while machine B occupies 1,200 sq.m of area and requires 8 men to operate it. The owner has 7,600 sq.m of area available and 72 men to operate the machines. If machine A produces 50 units and machine B produces 40 units daily, how many machines of each type should he buy to maximize the daily output? Use Linear Programming to find the solution.
View Solution
Knowledge Check
The power output of machine that lifts a 600 kg crate through a height of 20 m in 1 minute, is
A0.98 kWB1.96 kWC3.92 kWD12 kW
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the tune (in minutes) required for each toy on the machines is given below:
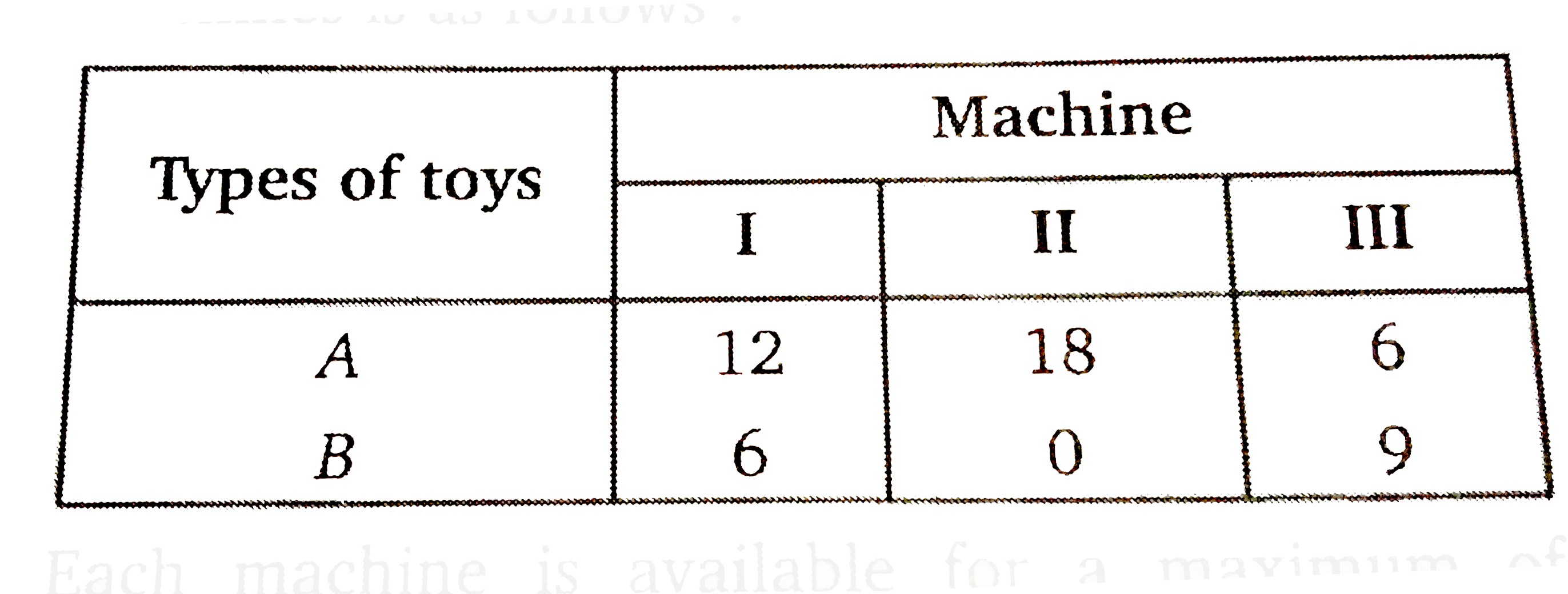 Each machine is available for a
maximum of 6 hours per day. If the profit
Each machine is available for a
maximum of 6 hours per day. If the profit
View SolutionIf 80 men can assemble 5 machines in a day, how many men are needed to assemble 7 machines in a day ?
View SolutionA manufacturer produces two types of steel trunks. He has tow machines A and B. For completing, the first types of the trunk requires 3 hours on machine A and 3 hours on machine B, whereas the second type of the trunk requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs. 30 and Rs. 25 per trunk of the first type and the second respectively. How many trunks of each type must he make each day to makes maximum profit?
View SolutionA factory requires 42 machines to produce a given number of articles in 63 days. How many machines would be required to produce the same number of articles in 54 days?
View SolutionRaghu has enough money to buy 75 machines worth Rs.200 each. How many machines can he buy if he gets a discount of Rs.50 on each machine ?
View SolutionManufacturer produces two types of steel trunks. He has two machines, A and B. The first type of trunk requires 3 hours on machine A and 3 hours on machine B. The second type requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs. 30 per trunk on the first type of trunk and Rs. 25 per trunk on the second type. Formulate a linear programming problem to find out how many trunks of each type he must make each day to maximize his profit.
View SolutionA machine in a soft drink factory fills 840 bottles in six hours. How many bottles will it fill in five hours?
View Solution
