A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at Rs. 7 profit and that of B at a profit of Rs. 4. Find the production level per day for maximum profit graphically.
To solve the problem step by step, we will follow the process of formulating the objective function, defining the constraints, graphing the feasible region, and finding the optimal solution.
Step 1: Define Variables
Let:
- x = number of units of product A produced per day
- y = number of units of product B produced per day
Step 2: Formulate the Objective Function
The profit from each unit of product A is Rs. 7 and from each unit of product B is Rs. 4. Therefore, the total profit z can be expressed as:
z=7x+4y
We want to maximize z.
Step 3: Define the Constraints
From the problem statement, we know the following:
1. Each unit of product A requires 3 hours on machine 1 and 3 hours on machine 2.
2. Each unit of product B requires 2 hours on machine 1 and 1 hour on machine 2.
3. The available capacity of machine 1 is 12 hours and machine 2 is 9 hours.
Thus, we can formulate the constraints as follows:
1. For machine 1:
3x+2y≤12
2. For machine 2:
3x+y≤9
3. Non-negativity constraints:
x≥0,y≥0
Step 4: Graph the Constraints
To graph the constraints, we need to find the intercepts for each equation.
For the first constraint 3x+2y=12:
- When x=0:
2y=12⇒y=6(Point: (0, 6))
- When y=0:
3x=12⇒x=4(Point: (4, 0))
For the second constraint 3x+y=9:
- When x=0:
y=9(Point: (0, 9))
- When y=0:
3x=9⇒x=3(Point: (3, 0))
Step 5: Identify the Feasible Region
Plot the lines on a graph and shade the feasible region that satisfies all constraints. The feasible region is bounded by the lines and the axes.
Step 6: Find Corner Points
The corner points of the feasible region can be found at the intersections of the lines and the axes:
1. (0,0)
2. (4,0)
3. (0,6)
4. Intersection of 3x+2y=12 and 3x+y=9:
- Solve the equations:
3x+2y=12(1)
3x+y=9(2)
Subtract (2) from (1):
y=3
Substitute y=3 into (2):
3x+3=9⇒3x=6⇒x=2(Point: (2, 3))
Step 7: Evaluate the Objective Function at Each Corner Point
Now we calculate z at each corner point:
1. At (0,0):
z=7(0)+4(0)=0
2. At (4,0):
z=7(4)+4(0)=28
3. At (0,6):
z=7(0)+4(6)=24
4. At (2,3):
z=7(2)+4(3)=14+12=26
Step 8: Determine Maximum Profit
The maximum profit occurs at the point (2,3) with a profit of Rs. 26.
Conclusion
The production level per day for maximum profit is:
- 2 units of product A
- 3 units of product B
Let:
- x = number of units of product A produced per day
- y = number of units of product B produced per day
The profit from each unit of product A is Rs. 7 and from each unit of product B is Rs. 4. Therefore, the total profit z can be expressed as:
z=7x+4y
We want to maximize z.
From the problem statement, we know the following:
1. Each unit of product A requires 3 hours on machine 1 and 3 hours on machine 2.
2. Each unit of product B requires 2 hours on machine 1 and 1 hour on machine 2.
3. The available capacity of machine 1 is 12 hours and machine 2 is 9 hours.
1. For machine 1:
3x+2y≤12
2. For machine 2:
3x+y≤9
3. Non-negativity constraints:
x≥0,y≥0
To graph the constraints, we need to find the intercepts for each equation.
- When x=0:
2y=12⇒y=6(Point: (0, 6))
- When y=0:
3x=12⇒x=4(Point: (4, 0))
- When x=0:
y=9(Point: (0, 9))
- When y=0:
3x=9⇒x=3(Point: (3, 0))
Plot the lines on a graph and shade the feasible region that satisfies all constraints. The feasible region is bounded by the lines and the axes.
The corner points of the feasible region can be found at the intersections of the lines and the axes:
1. (0,0)
2. (4,0)
3. (0,6)
4. Intersection of 3x+2y=12 and 3x+y=9:
- Solve the equations:
3x+2y=12(1)
3x+y=9(2)
Subtract (2) from (1):
y=3
Substitute y=3 into (2):
3x+3=9⇒3x=6⇒x=2(Point: (2, 3))
Now we calculate z at each corner point:
1. At (0,0):
z=7(0)+4(0)=0
2. At (4,0):
z=7(4)+4(0)=28
3. At (0,6):
z=7(0)+4(6)=24
4. At (2,3):
z=7(2)+4(3)=14+12=26
The maximum profit occurs at the point (2,3) with a profit of Rs. 26.
The production level per day for maximum profit is:
- 2 units of product A
- 3 units of product B
Topper's Solved these Questions
Similar Questions
Simple machines
View Solution
Explain how each of these machines work.View SolutionIf machine is lubricated with oil
View SolutionA company sells two different products A and B. The two products are produced in a common production process and are sold in two different markets. The production process has a total capacity of 45000 man-hours. It takes 5 hours to produce a unit of A and 3 hours to produce a unit of B. The market has been surveyed and company officials feel that the maximum number of units of A that can be sold is 7000 ad that of B is 10,000. If the profit is Rs. 60 per unit for the product A and Rs. 40 per unit for the product B, how many units of each product should be sold to maximize profit? Formulate the problem as LPP.
View SolutionA manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the tune (in minutes) required for each toy on the machines is given below:
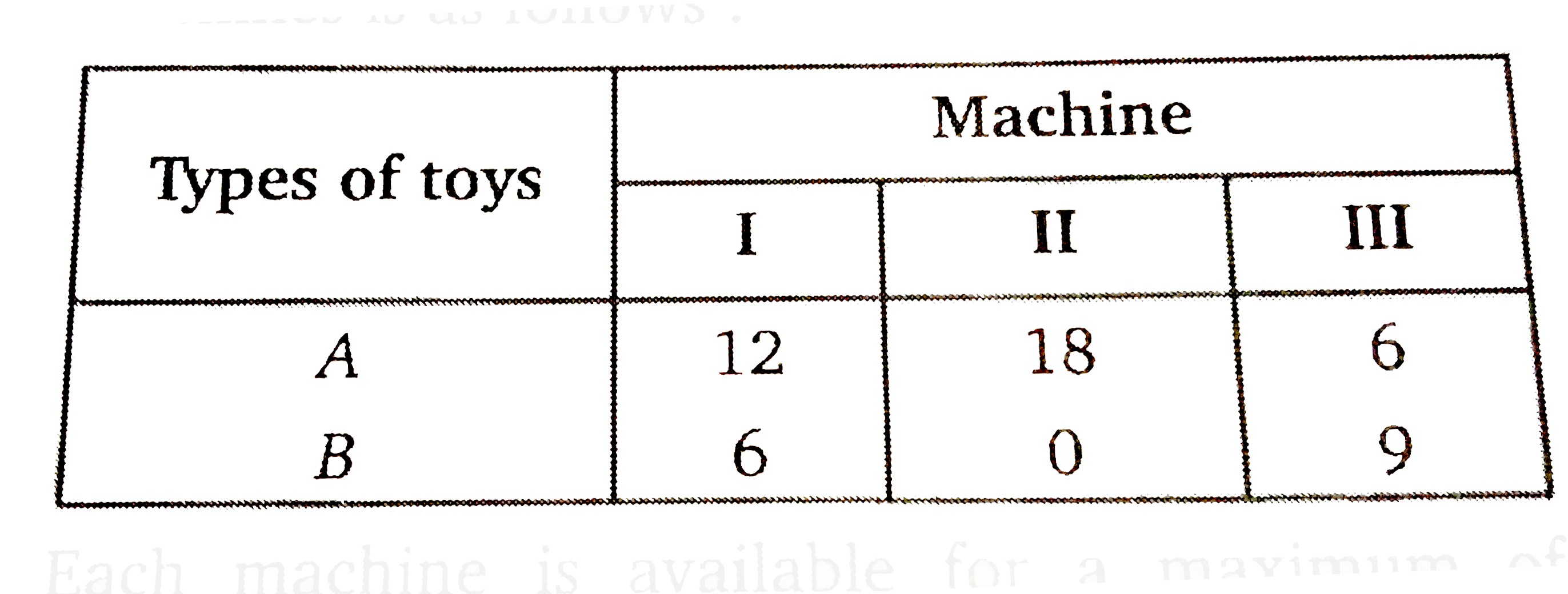 Each machine is available for a
maximum of 6 hours per day. If the profit View Solution
Each machine is available for a
maximum of 6 hours per day. If the profit View SolutionA machine does 392 J of work in 4 seconds. What is the power of the machine?
View SolutionA firm manufactures two products A and B. Each product is processed on two machines M1andM2 . Product A requires 4 minutes of processing time on M1 and 8 min. on M2 ; product B requires 4 minutes on M1 and 4 min. on M2 . The machine M1 is available for not more than 8 hrs 20 min. while machine M2 is available for 10 hrs. during any working day. The products A and B are sold at a profit of Rs. 3 and Rs. 4 respectively. Formulate the problem as a linear programming problem and find how many products of each type should be produced by the firm each day in order to get maximum profit.
View SolutionA company sells two different products, A and B. The two products are produced in a common production process, which has a total capacity of 500 man-hours. It takes 5 hours to produce a unit of A and 3 hours to produce a unit of B. The market has been surveyed and company officials feel that the maximum number of units of A that can be sold is 70 and that, for B is 125. If the profit is Rs. 20 per unit for the product A and Rs. 15 per unit for the product B, how many units of each product should be sold to maximize profit?
View SolutionA manufacturer produces two types of steel trunks. He has tow machines A and B. For completing, the first types of the trunk requires 3 hours on machine A and 3 hours on machine B, whereas the second type of the trunk requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs. 30 and Rs. 25 per trunk of the first type and the second respectively. How many trunks of each type must he make each day to makes maximum profit?
View SolutionIf , a machine gun fires n bullets per second each with kinetic energy K, then the power of the machine gun is
View Solution

