A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes 1 hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is Rs 100 and that on a bracelet is Rs 300, how many of each should be produced daily to maximize the profit?
To solve the problem of maximizing profit from the production of necklaces and bracelets, we will follow these steps:
Step 1: Define Variables
Let:
- x = number of necklaces produced
- y = number of bracelets produced
Step 2: Set Up Constraints
1. The total number of necklaces and bracelets that can be produced per day is at most 24:
x+y≤24(Constraint 1)
2. The time taken to produce necklaces and bracelets is limited by the available hours:
- It takes 0.5 hours to make a necklace and 1 hour to make a bracelet.
- The total available hours per day is 16 hours:
x2+y≤16(Constraint 2)
This can be rewritten as:
x+2y≤32(after multiplying by 2)
Step 3: Set Up the Objective Function
The profit from producing necklaces and bracelets is given by:
- Profit from necklaces = Rs 100 per necklace
- Profit from bracelets = Rs 300 per bracelet
Thus, the objective function to maximize profit Z is:
Z=100x+300y
Step 4: Identify Non-negativity Constraints
Since we cannot produce a negative number of items, we have:
x≥0,y≥0
Step 5: Graph the Constraints
To graph the constraints, we will find the intercepts for each equation.
1. For x+y=24:
- If x=0, then y=24 (Point: (0, 24))
- If y=0, then x=24 (Point: (24, 0))
2. For x+2y=32:
- If x=0, then y=16 (Point: (0, 16))
- If y=0, then x=32 (Point: (32, 0))
Step 6: Find the Feasible Region
Plot the lines on a graph and shade the feasible region that satisfies both constraints. The feasible region is bounded by the axes and the lines.
Step 7: Find Corner Points
The corner points of the feasible region can be found by solving the equations:
1. Intersection of x+y=24 and x+2y=32:
- From x+y=24, we can express y=24−x.
- Substitute into x+2(24−x)=32:
x+48−2x=32⟹−x+48=32⟹x=16
- Substitute x=16 back to find y:
y=24−16=8
- So, one corner point is (16,8).
2. Other corner points are:
- (0,24)
- (24,0)
- (0,16)
Step 8: Evaluate the Objective Function at Each Corner Point
1. For (0,24):
Z=100(0)+300(24)=7200
2. For (16,8):
Z=100(16)+300(8)=1600+2400=4000
3. For (24,0):
Z=100(24)+300(0)=2400
4. For (0,16):
Z=100(0)+300(16)=4800
Step 9: Determine Maximum Profit
The maximum profit occurs at the point (0,24) with a profit of Rs 7200. However, since the production of necklaces and bracelets must be considered, we need to check the feasible solutions.
Conclusion
The optimal solution is to produce:
- 16 necklaces
- 8 bracelets
This combination maximizes the profit while adhering to the constraints.
Let:
- x = number of necklaces produced
- y = number of bracelets produced
1. The total number of necklaces and bracelets that can be produced per day is at most 24:
x+y≤24(Constraint 1)
- It takes 0.5 hours to make a necklace and 1 hour to make a bracelet.
- The total available hours per day is 16 hours:
x2+y≤16(Constraint 2)
This can be rewritten as:
x+2y≤32(after multiplying by 2)
The profit from producing necklaces and bracelets is given by:
- Profit from necklaces = Rs 100 per necklace
- Profit from bracelets = Rs 300 per bracelet
Z=100x+300y
Since we cannot produce a negative number of items, we have:
x≥0,y≥0
To graph the constraints, we will find the intercepts for each equation.
- If x=0, then y=24 (Point: (0, 24))
- If y=0, then x=24 (Point: (24, 0))
- If x=0, then y=16 (Point: (0, 16))
- If y=0, then x=32 (Point: (32, 0))
Plot the lines on a graph and shade the feasible region that satisfies both constraints. The feasible region is bounded by the axes and the lines.
The corner points of the feasible region can be found by solving the equations:
1. Intersection of x+y=24 and x+2y=32:
- From x+y=24, we can express y=24−x.
- Substitute into x+2(24−x)=32:
x+48−2x=32⟹−x+48=32⟹x=16
- Substitute x=16 back to find y:
y=24−16=8
- So, one corner point is (16,8).
- (0,24)
- (24,0)
- (0,16)
1. For (0,24):
Z=100(0)+300(24)=7200
2. For (16,8):
Z=100(16)+300(8)=1600+2400=4000
3. For (24,0):
Z=100(24)+300(0)=2400
4. For (0,16):
Z=100(0)+300(16)=4800
The maximum profit occurs at the point (0,24) with a profit of Rs 7200. However, since the production of necklaces and bracelets must be considered, we need to check the feasible solutions.
The optimal solution is to produce:
- 16 necklaces
- 8 bracelets
Topper's Solved these Questions
Similar Questions
A small firm manufactures items A and B. The total number of items that it can manufacture in a day is at the most 24 Item A takes on hour to make while item B takes only half an hour. The maximum time available per day is 16 hours. If the profit on one unit of item A be 300 and that on one unit of item B be 160, how many of each type of item should be produced to maximize the profit? Solve the problem graphically
View SolutionWhat percent of a day is half an hour ?
View SolutionA manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs 17.50 per package on nuts and Rs 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machine for at most 12 hours a day?
View SolutionA manufacturer produces nuts and bolts. It takes 2 hours work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 2 hours on machine B to produce a package of bolts. He earns a profit of Rs. 24 per package on nuts and Rs. 18 per package on bolts. How many packages of each should be produced each day so as to maximize his profit, if he operates his machines for at the most 10 hours a day. Make an L.P.P. from above and solve it graphically ?
View SolutionThe number of ways in which 5 beads of different colours can be made into a necklace is
View SolutionA manufacturer manufactures two types of tea-cups, A and B. Three machines are needed for manufacturing the tea cups. The time in minutes required for manufacturing each cup on the machines is given below:
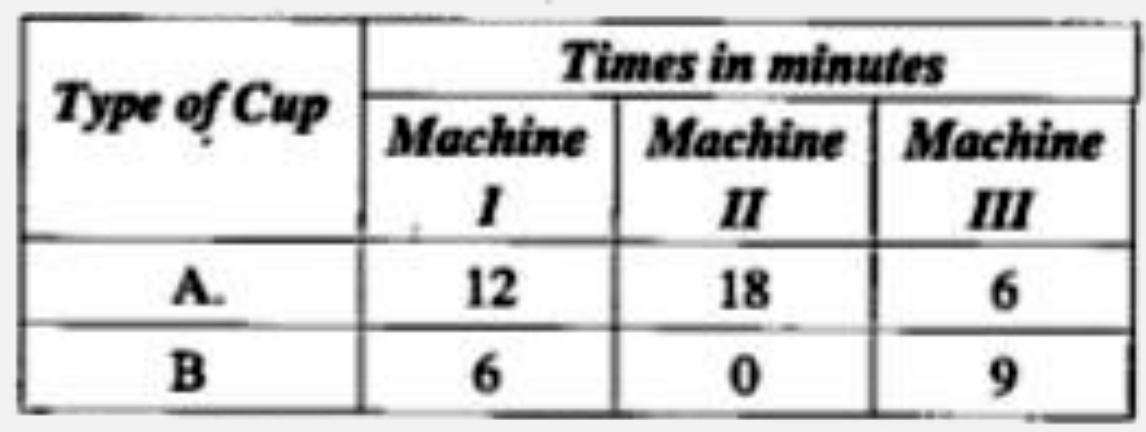
Each machine is available for a maximum of six hours per day. If the profit on each cup of type A is Rs 1.50and that'on each cup of type B is Rs 1.00, find the number of cups of each type that should be manufactured in a day to get maximumprofit.
View SolutionNumber of necklaces can be formed with 4 identical beads and two distinct jewels is 'k', then k divides
View SolutionA manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each purpose and the time (in minutes) required for each toy on the machines is given below:
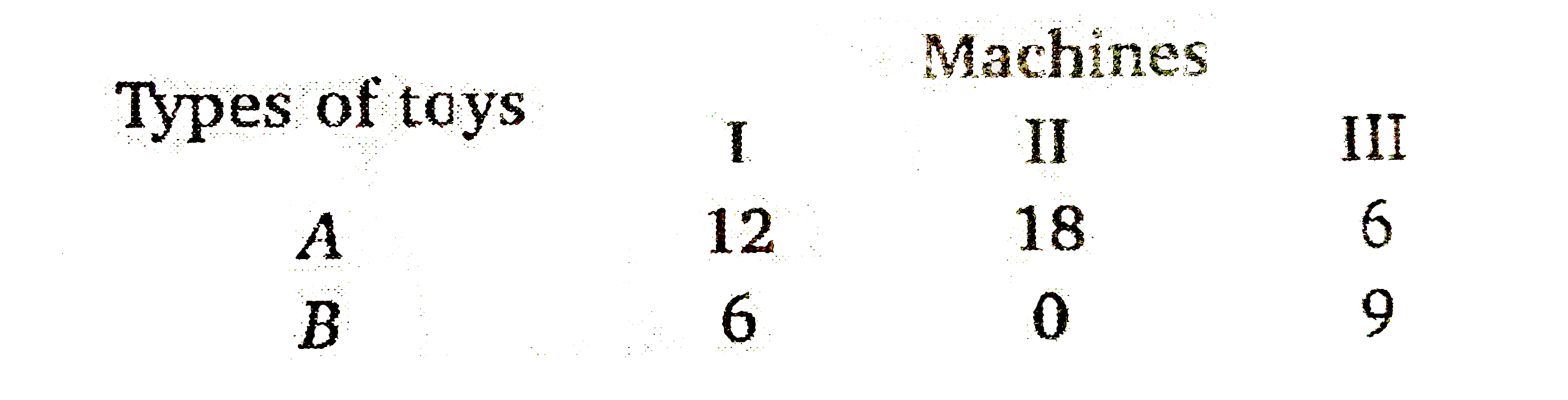
Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs. 7.50 and that on each toy of type B is Rs. 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
View SolutionFind the number of ways in which 10 different diamonds can be arranged to make a necklace.
View SolutionFind number of ways that 8 beads of different colors be strung as a necklace.
View Solution
