A company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours for assembling. The profit is Rs 5 each for type A and Rs 6 each for type B souvenirs. How many souvenirs of each type should the company manufacture m order to maximise the profit?
To solve the problem, we will follow these steps:
Step 1: Define the Variables
Let:
- x = number of type A souvenirs manufactured
- y = number of type B souvenirs manufactured
Step 2: Identify the Time Constraints
From the problem, we know:
- Type A requires 5 minutes for cutting and 10 minutes for assembling.
- Type B requires 8 minutes for cutting and 8 minutes for assembling.
The total time available for cutting is 3 hours 20 minutes, which is:
3×60+20=200 minutes
The total time available for assembling is 4 hours, which is:
4×60=240 minutes
Step 3: Formulate the Inequalities
Based on the time requirements and available time, we can set up the following inequalities:
1. For cutting:
5x+8y≤200
2. For assembling:
10x+8y≤240
Step 4: Find the Intercepts
To graph these inequalities, we need to find the intercepts.
For the first inequality 5x+8y=200:
- If x=0:
8y=200⟹y=25
- If y=0:
5x=200⟹x=40
For the second inequality 10x+8y=240:
- If x=0:
8y=240⟹y=30
- If y=0:
10x=240⟹x=24
Step 5: Plot the Points
The intercepts are:
- For 5x+8y=200: (0, 25) and (40, 0)
- For 10x+8y=240: (0, 30) and (24, 0)
Step 6: Find the Intersection of the Lines
To find the intersection of the lines represented by the equations, we can solve the system of equations:
1. 5x+8y=200
2. 10x+8y=240
Subtracting the first equation from the second:
(10x+8y)−(5x+8y)=240−200
5x=40⟹x=8
Substituting x=8 back into the first equation:
5(8)+8y=200
40+8y=200
8y=160⟹y=20
So, the intersection point is (8,20).
Step 7: Identify the Feasible Region
The feasible region is bounded by the points:
- (0, 25)
- (8, 20)
- (24, 0)
- (0, 30)
Step 8: Calculate the Profit
The profit function is:
Z=5x+6y
We will evaluate the profit at each vertex of the feasible region:
1. At (0, 25):
Z=5(0)+6(25)=150
2. At (8, 20):
Z=5(8)+6(20)=40+120=160
3. At (24, 0):
Z=5(24)+6(0)=120
Step 9: Determine Maximum Profit
The maximum profit occurs at the point (8,20) with a profit of Rs 160.
Conclusion
To maximize profit, the company should manufacture:
- 8 souvenirs of type A
- 20 souvenirs of type B
Let:
- x = number of type A souvenirs manufactured
- y = number of type B souvenirs manufactured
From the problem, we know:
- Type A requires 5 minutes for cutting and 10 minutes for assembling.
- Type B requires 8 minutes for cutting and 8 minutes for assembling.
3×60+20=200 minutes
4×60=240 minutes
Based on the time requirements and available time, we can set up the following inequalities:
5x+8y≤200
10x+8y≤240
To graph these inequalities, we need to find the intercepts.
- If x=0:
8y=200⟹y=25
- If y=0:
5x=200⟹x=40
- If x=0:
8y=240⟹y=30
- If y=0:
10x=240⟹x=24
The intercepts are:
- For 5x+8y=200: (0, 25) and (40, 0)
- For 10x+8y=240: (0, 30) and (24, 0)
To find the intersection of the lines represented by the equations, we can solve the system of equations:
2. 10x+8y=240
(10x+8y)−(5x+8y)=240−200
5x=40⟹x=8
5(8)+8y=200
40+8y=200
8y=160⟹y=20
The feasible region is bounded by the points:
- (0, 25)
- (8, 20)
- (24, 0)
- (0, 30)
The profit function is:
Z=5x+6y
1. At (0, 25):
Z=5(0)+6(25)=150
2. At (8, 20):
Z=5(8)+6(20)=40+120=160
3. At (24, 0):
Z=5(24)+6(0)=120
The maximum profit occurs at the point (8,20) with a profit of Rs 160.
To maximize profit, the company should manufacture:
- 8 souvenirs of type A
- 20 souvenirs of type B
Topper's Solved these Questions
Similar Questions
A company manufactures two types of toys A and B. A toy of type A requires 5 minute for cutting and 10 minute for assembling. A toy of type B requires 8 minute for cutting and 8 minutes for assembling. There are 3 hours available for cutting and 4 hours available for assembling th etoys in a day. The profit is Rs 50 each on a toy of Type A and Rs 60 each on a toy of type B. How many toys of each type should the company manufacture in a day to maximize the profit ? Use linear programming to find the solution.
View SolutionA company manufactures two types of products A and B. Each unit of A requires 3 grams of nickel and 1 gram of chromium, while each unit of B requires 1 gram of nickel and 2 grams of chromium. The firm can produce 9 grams of nickel and 8 grams of chromium. The profit is Rs. 40 on each unit of product of type A and Rs. 50 on each unit of type B. How many units of each type should the company manufacture so as to earn maximum profit ? Use linear programming to find the solution.
View SolutionWhat fraction of an hour is 20 minutes?
View SolutionWhat fractions is:
36 minutes of 2 hours?
View SolutionWhat fractions is:
54 minutes of 2 hours?
View SolutionFind the ratio of :
5 hours and 50 minutes to 8 hours and 10 minutes.
View SolutionA manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each purpose and the time (in minutes) required for each toy on the machines is given below:
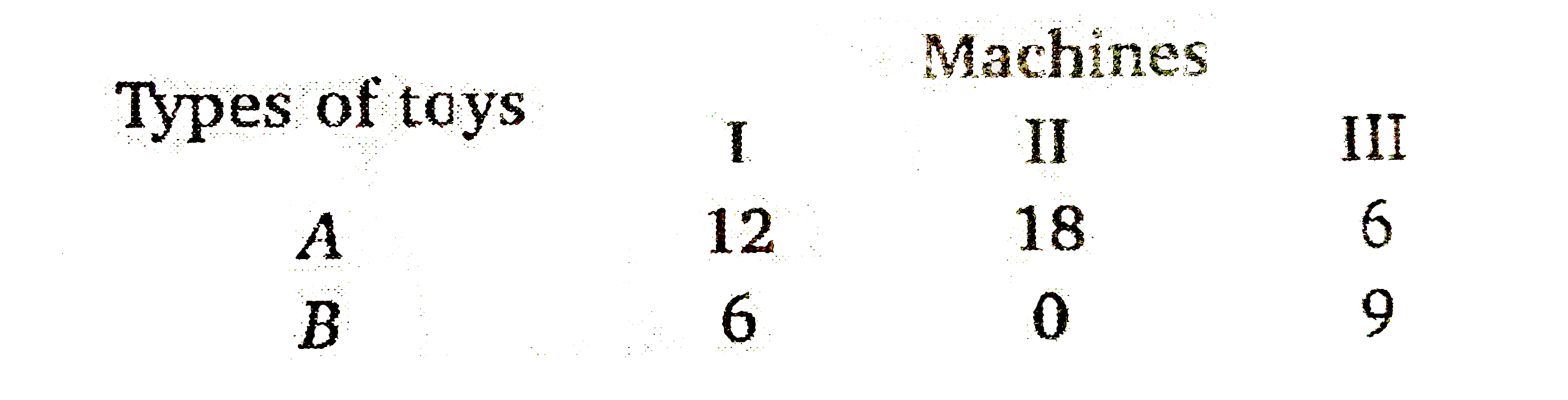
Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs. 7.50 and that on each toy of type B is Rs. 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
View SolutionA manufacturing companu makes two types of teaching aids A and B of Mathematics for Class X. Each type of A requires 9 labour hours for fabircating and 1 labour for finishing. Each type of B requires 12 labour hours for fabircating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available per week are 180 and 30 respectively. The company makes a profit of 80 on each piece of type A and 120 on each piece of type B. How many pieces of type A and types B should be manufactured per week to get a maximum profit? Formulae this as Linear Programming Problems and solved it. Identify the feasible region from the rough sketch.
View Solutionminute , hour , second are ?
View SolutionWhat fraction of an hour is 40 minutes?
View Solution
