The corner points of the feasible region of an LPP are (0,0), (0,8), (2,7),(5,4),and (6,4). the maximum profit P= 3x + 2y occurs at the point_____.
Step by step video & image solution for The corner points of the feasible region of an LPP are (0,0), (0,8), (2,7),(5,4),and (6,4). the maximum profit P= 3x + 2y occurs at the point_____. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Corner points of the feasible region for an LPP are (0,2),(3,0),(6,0),(6,8), and (0,5). Let F-4x+6y be the objective function. Determine the minimum valur of F occurs at
View SolutionCorner points of the feasible region for an LPP are ( 0,2) (3,0) ,(6,0),(6,8) and (0,5) Let Z=4 x + 6y be the objective function. The minimum value of F occurs at?
View Solution
Knowledge Check
If the corner points of the feasible region for an LPP are (0,2),(3,0),(6,0),(6,8),(0,5) then maximum of F - minimum of F =
A60B48C42D18If the objective function for a L.P.P. is Z=5x+7y and the corner points of the bounded feasible region are (0, 0), (7, 0), (3, 4) and (0, 2), then the maximum value of Z occurs at
AA) (0, 0)BB) (7, 0)CC) (3, 4)DD) (0, 2)If the corner points of the feasible region for an L.P.P. are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5), then the minimum value of the objective function F=4x+6y occurs at
AA) (0, 2) onlyBB) (3, 0) onlyCC) the mid-point of the line segment joining the point (0, 2) and (3, 0) onlyDD) every point on the line segment joining the point (0, 2) and (3, 0)
In the following the feasible region (shaded) for a LPP is shown Determine the maximum and minimum value of Z=x+2y
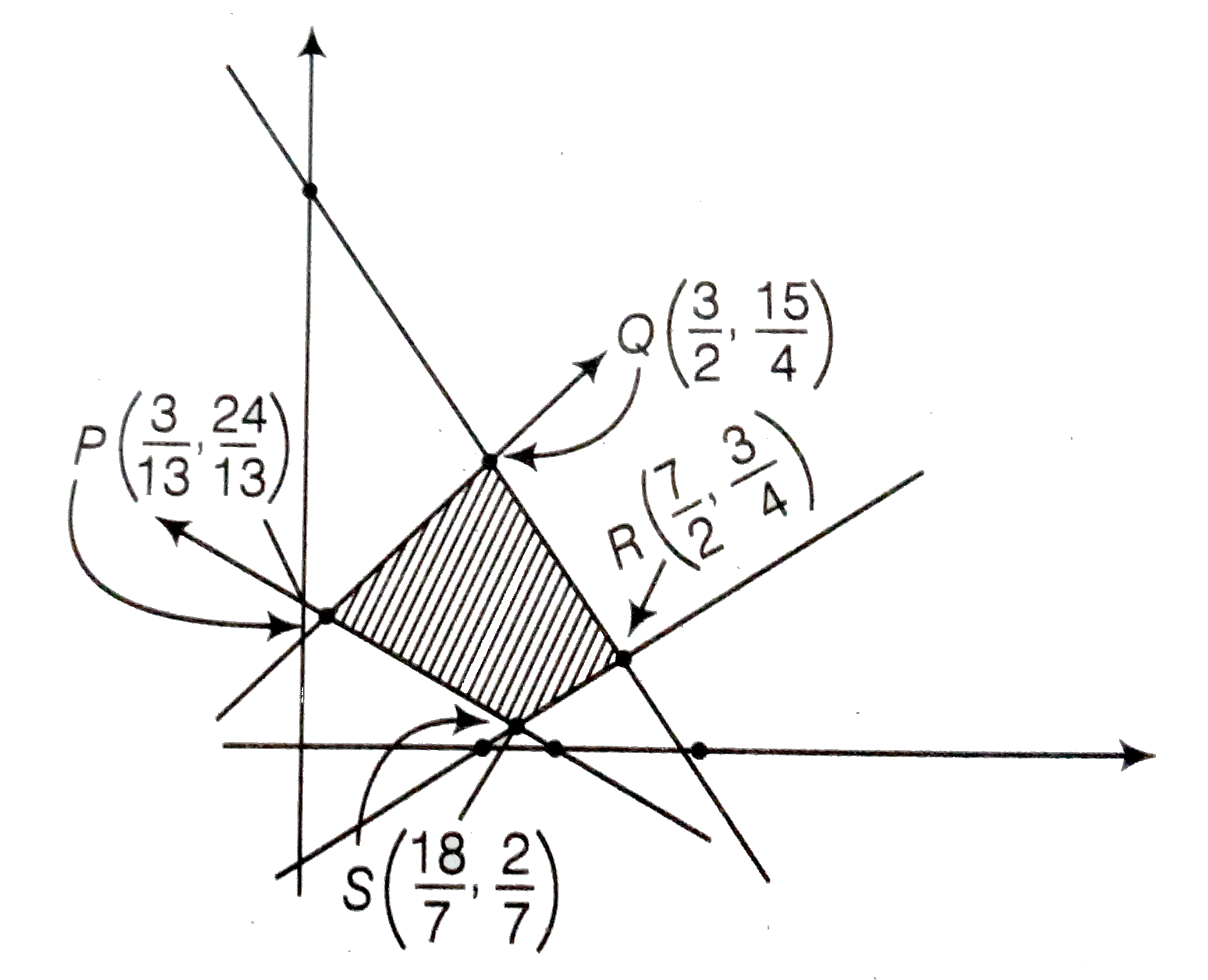
View SolutionIf the objective function for an L.P.P. is Z=3x+4y and the corner points for unbounded feasible region are (9, 0), (4, 3), (2, 5), and (0, 8), then the maximum value of Z occurs at
View SolutionIf the objective function for an L.P.P. is Z=3x−4y and the corner points for the bounded feasible region are (0, 0), (5, 0), (6, 5), (6, 8), (4, 10) and (0, 8), then the maximum value of Z occurs at
View SolutionThe occurs point of the feasible region for an L.P.P. are (0, 3), (1, 1) and (3, 0). If objective function is Z=px+qy,p,q>0, then the condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is
View SolutionThe corner points of the feasible region determine by the system of linear constrainsts are (0,10) ,(5,5) ,(15,15),(0,20),Let Z=px +qy , where p,q>0. Conditions on p and q so that the maximum of Z occurs at the point (15,15) and (0,20) is
View Solution
