(a) For a ray of light travelling from a denser medium of refractive index n1 to a rarer medium of refractive index n2, prove that n2n1=sinic, where ic is the critical angle of incidence for the media.
(b) Explain with the help of a diagram, how the above principle is used for transmission of video signals using optical fibers.
Solution:
(a) To prove that n2n1=sinic, where ic is the critical angle of incidence for light traveling from a denser medium (refractive index n1) to a rarer medium (refractive index n2), we can use Snell's Law.
1. Understanding Snell's Law: Snell's Law states that:
n1sini=n2sinr
where i is the angle of incidence and r is the angle of refraction.
2. Critical Angle Definition: The critical angle ic is defined as the angle of incidence at which the angle of refraction r becomes 90∘. This means that the light ray travels along the boundary between the two media.
3. Applying Snell's Law at Critical Angle: At the critical angle, we can substitute r=90∘ into Snell's Law:
n1sinic=n2sin90∘
4. Simplifying the Equation: Since sin90∘=1, we can simplify the equation to:
n1sinic=n2
5. Rearranging the Equation: Rearranging this gives us:
n2n1=sinic
Thus, we have proved that:
n2n1=sinic
---
(b) To explain how the principle of total internal reflection is used for the transmission of video signals using optical fibers, we can follow these steps:
1. Structure of Optical Fiber: An optical fiber consists of a core and cladding. The core has a higher refractive index n1 and the cladding has a lower refractive index n2 (i.e., n1>n2).
2. Light Transmission: When light enters the core of the optical fiber, it travels through the core and strikes the boundary between the core and cladding at an angle of incidence I.
3. Total Internal Reflection: If the angle of incidence I is greater than the critical angle ic, the light does not refract into the cladding but instead reflects back into the core. This phenomenon is known as total internal reflection.
4. Diagram Explanation: (A diagram would typically show the core and cladding, the incident light ray, the normal line, and the angles of incidence and reflection.)
5. Signal Transmission: This principle allows light signals to be transmitted through the fiber with minimal loss, as the light continues to reflect within the core without escaping into the cladding.
6. Applications: Optical fibers are widely used in telecommunications and data transmission, allowing for high-speed internet and video signal transmission over long distances.
---
n1sini=n2sinr
where i is the angle of incidence and r is the angle of refraction.
n1sinic=n2sin90∘
n1sinic=n2
n2n1=sinic
n2n1=sinic
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET I
54 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET II
8 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
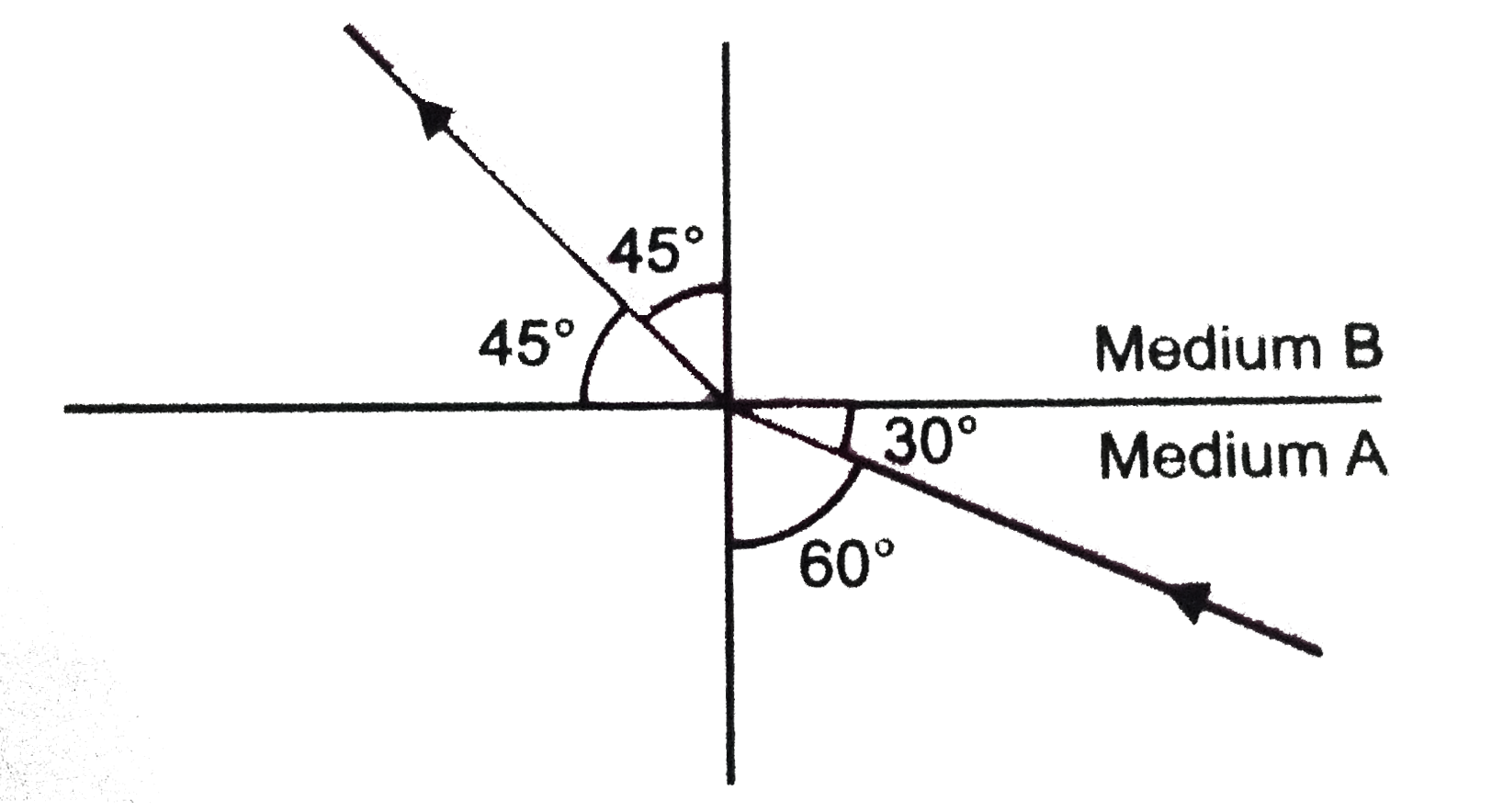
Figure shows a ray of light as it travels from medium A to medium B. Refractive index of the medium B relative to medium A is
View SolutionA biconvex thin lens is prepared from glass of refractive index μ2=32. The two conducting surfaces have equal radii of 20 cm each. One of the the surface is silvered from outside to make it reflecting. It is placed in a medium of refractive index μ1=53. It acts as a
View Solution
Knowledge Check
When a light ray enters from a denser medium to a rarer medium.
AThe light ray bends towards the normal.BAngle of incidence is less than angle of refraction.CSpeed of light decreases.DSpeed of light remains unchanged.
When a light ray from a rarer medium is refracted into a denser medium, its
View SolutionA ray of light passes from a medium A having refractive index 1.6 to the medium B having refractive index 1.5. The value of critical angle of medium
A is….
View SolutionWhen a ray of light travels obliquely from a rarer medium to a denser medium, it bends away from the normal.
View Solution(a) Obtain lens makers formula using the expression
n2v−n1u=(n2−n1)R
Here the ray of light propagating from a rarer medium of refractive index (n1) to a denser medium of refractive index (n2) is incident on the convex side of sperical refracting surface of radius of curvature R.
(b) Draw a ray diagram to show the umage formation by concave mirror when the object is kept between its focus and the pole. Using this diagram, derive the magnification formula for the image formed.
View SolutionHow is the critical angle related to the refractive index of a medium ?
View SolutionA beam of monochromatic light is refracted from vacuum into a medium of refractive index 1.5 The wavelength of refracted light will be
View SolutionA ray of light passes from vaccum into a medium of refractive index n. If the angle of incidence is twice the angle of refraction, then the angle of incidence is
View Solution
