A beam of monochromatic light is refracted from vacuum into a medium of refractive index 1.5 The wavelength of refracted light will be
dependent on intensity of refracted light
same
smaller
large
The correct Answer is:C
To solve the problem of finding the wavelength of light refracted from vacuum into a medium with a refractive index of 1.5, we can follow these steps:
1. Understanding the Problem:
- We have a beam of monochromatic light (which means it has a single wavelength) that is traveling from vacuum into a medium with a refractive index (μ) of 1.5.
2. Refractive Index Definition:
- The refractive index (μ) is defined as the ratio of the speed of light in vacuum (C) to the speed of light in the medium (V):
μ=CV
- Here, C is approximately 3×108m/s.
3. Relationship Between Wavelength and Refractive Index:
- When light travels from one medium to another, its frequency (ν) remains constant, but its speed and wavelength change. The relationship can be expressed as:
V=λ⋅ν
- Therefore, when light enters a medium with a refractive index, the new wavelength (λ') in the medium can be calculated using:
λ′=λμ
- Here, λ is the original wavelength in vacuum.
4. Calculating the New Wavelength:
- Given that the refractive index (μ) is 1.5, we can substitute this into our equation:
λ′=λ1.5
- This shows that the wavelength in the medium will be smaller than the wavelength in vacuum.
5. Conclusion:
- The wavelength of the refracted light will be λ1.5.
Final Answer:
- The wavelength of the refracted light in the medium is λ1.5.
- We have a beam of monochromatic light (which means it has a single wavelength) that is traveling from vacuum into a medium with a refractive index (μ) of 1.5.
- The refractive index (μ) is defined as the ratio of the speed of light in vacuum (C) to the speed of light in the medium (V):
μ=CV
- Here, C is approximately 3×108m/s.
- When light travels from one medium to another, its frequency (ν) remains constant, but its speed and wavelength change. The relationship can be expressed as:
V=λ⋅ν
- Therefore, when light enters a medium with a refractive index, the new wavelength (λ') in the medium can be calculated using:
λ′=λμ
- Here, λ is the original wavelength in vacuum.
- Given that the refractive index (μ) is 1.5, we can substitute this into our equation:
λ′=λ1.5
- This shows that the wavelength in the medium will be smaller than the wavelength in vacuum.
- The wavelength of the refracted light will be λ1.5.
- The wavelength of the refracted light in the medium is λ1.5.
Similar Questions
A beam o monochromatic light of wavelength λ is reflected from air into water to refractive index 4/3. The wavelength of light beam inside water will be
View SolutionMonochromatic light is refracted from air into the glass of refractive index μ . The ratio of the wavelength of incident and refracted waves is
View SolutionWhen light is refracted into a medium
View SolutionWhen light is refracted into a medium
View SolutionA beam of menochromatic blue light of wavelength 4200 Ål in air travels in water of refractive index 4/3. its wavelength in water will be
View SolutionA ray of light passes from vaccum into a medium of refractive index n. If the angle of incidence is twice the angle of refraction, then the angle of incidence is
View SolutionIn YDSE shown in figure a parallel beam of light is incident on the slits from a medium of refractive index n1. The wavelength of light in this medium is λ1. A transparent slab of thickness t and refractive index n3 is put in front of one slit. The medium between the screen and the plane of the slits is n2. The phase difference between the light waves reaching point O (symmetrical, relative to the slits) is
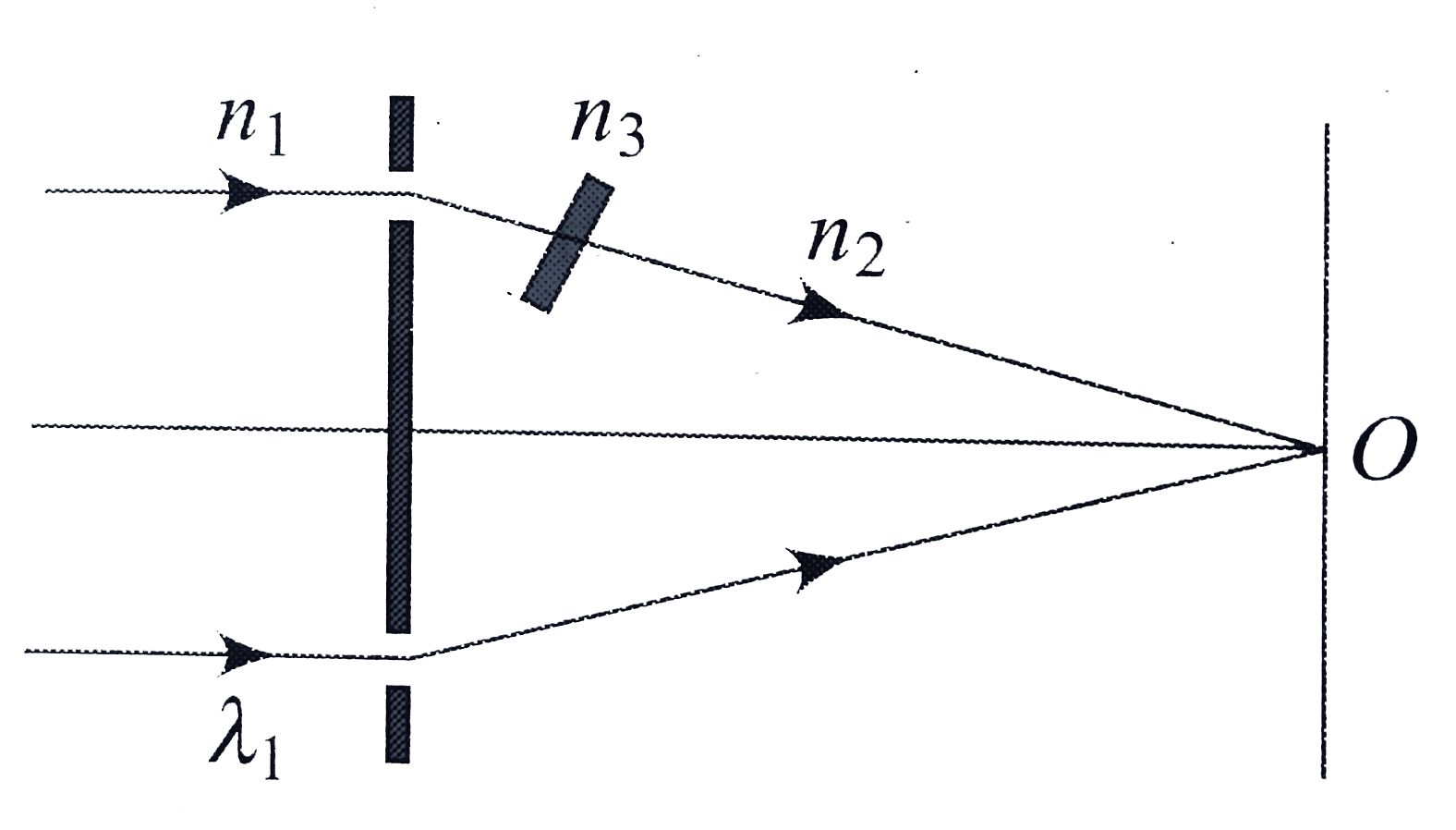
View SolutionMonochromatic light of frequency 5×1012Hz travelling in vaccum enters a medium at refractive Index 15 Its wavelength in medium will be
View SolutionA monochromatic beam of light of wavelength 6000A in vacuum enters a medium of refractive index 1.5. In the medium its wavelength is…., its frequency is…..
View SolutionA monochromatic beam of light of wavelength λ and frequency v goes from vacum to a medium of refractive index n. How do the wavelength and frequency of light change ?
View Solution