Describe briefly, with the help of a labell diagram, the basic elements of an A.C. generator. State its underlying principle. Show diagrammatically how an alternating emf is generated by a loop of wire rotating in a magnetic field. Write the expression for the instantaneous value of emf induced in the rotating loop.
Step-by-Step Solution:
Step 1: Basic Elements of an A.C. Generator
An A.C. generator, also known as an alternator, consists of four main components:
1. Field Magnet: This is a strong magnet that creates a magnetic field. It has a North (N) and South (S) pole.
2. Armature: The armature is a coil of wire (often made of insulated copper) wound around a soft iron core. It rotates within the magnetic field created by the field magnet.
3. Slip Rings: These are conductive rings attached to the ends of the armature. They rotate along with the armature and allow the generated current to be transferred out of the generator.
4. Brushes: These are made of conductive material (often carbon) and are in contact with the slip rings. They collect the alternating current (A.C.) produced in the armature and deliver it to an external circuit.
Step 2: Underlying Principle of A.C. Generator
The underlying principle of an A.C. generator is based on Faraday's Law of Electromagnetic Induction, which states that a change in magnetic flux through a circuit induces an electromotive force (emf) in the circuit. When the armature rotates in the magnetic field, the magnetic flux linked with the coil changes, leading to the generation of an induced emf.
Step 3: Diagrammatic Representation of A.C. Generation
To illustrate how an alternating emf is generated, consider a rectangular loop of wire rotating in a uniform magnetic field:
- Diagram Description:
- Draw a rectangular loop (ABCD) with the sides labeled A, B, C, and D.
- Show the magnetic field lines directed from the North pole to the South pole of the field magnet.
- Indicate the direction of rotation of the loop (clockwise or counterclockwise).
- Mark the angles at which the loop is positioned relative to the magnetic field.
Step 4: Expression for Instantaneous Value of Induced EMF
The instantaneous value of the induced emf (E) in the rotating loop can be expressed mathematically as:
E=−dΦdt
Where:
- Φ is the magnetic flux given by Φ=B⋅A⋅cos(θ)
- B is the magnetic field strength,
- A is the area of the loop,
- θ is the angle between the magnetic field and the normal to the plane of the loop.
As the loop rotates, θ changes with time, leading to:
E=−N⋅B⋅A⋅d(cos(θ))dt
Using θ=ωt (where ω is the angular velocity), we can derive:
E=N⋅B⋅A⋅ω⋅sin(ωt)
Where:
- N is the number of turns in the coil,
- ω=2πf (where f is the frequency of rotation).
An A.C. generator, also known as an alternator, consists of four main components:
2. Armature: The armature is a coil of wire (often made of insulated copper) wound around a soft iron core. It rotates within the magnetic field created by the field magnet.
The underlying principle of an A.C. generator is based on Faraday's Law of Electromagnetic Induction, which states that a change in magnetic flux through a circuit induces an electromotive force (emf) in the circuit. When the armature rotates in the magnetic field, the magnetic flux linked with the coil changes, leading to the generation of an induced emf.
To illustrate how an alternating emf is generated, consider a rectangular loop of wire rotating in a uniform magnetic field:
- Draw a rectangular loop (ABCD) with the sides labeled A, B, C, and D.
- Show the magnetic field lines directed from the North pole to the South pole of the field magnet.
- Indicate the direction of rotation of the loop (clockwise or counterclockwise).
- Mark the angles at which the loop is positioned relative to the magnetic field.
The instantaneous value of the induced emf (E) in the rotating loop can be expressed mathematically as:
- Φ is the magnetic flux given by Φ=B⋅A⋅cos(θ)
- B is the magnetic field strength,
- A is the area of the loop,
- θ is the angle between the magnetic field and the normal to the plane of the loop.
- N is the number of turns in the coil,
- ω=2πf (where f is the frequency of rotation).
Similar Questions
Obtain an expression for the instantaneous value of the induced emf in an ac generator.
View SolutionDraw a schematic sketch of an generator describing its basic elements. State briefly its working principle. Show a plot of variation of
(i) Magnetic flux and
(ii) Alternating emf versus time generated by a loop of wire rotating in a magnetic field.
(b) Why is choke coil needed in the use of fluorescent tubes with ac mains?
View SolutionExplain briefly, with the help of a labelled diagram, the basic principle of working of an a.c. generator. In an a.c. generator, coil of N turns and area A rotating with a constant angular speed ω in a uniform magnetic field B. Write the expression for the emf produced.
A 100-turn coil of area 0.1m2 rotates at half a revolution per second. It is placed in a magnetic field 0.01 T perpendicular to the axis of rotation of the coil. Calculate the maximum voltage generated in the coil.
View Solution(a) Draw a schematic diagram of an AC generator. Explain is working and obtain the expression for the instantaneous value of the emf in terms of the magnetic field B, number of turns N of the coil of area A rotating with angular frequency ω. Show how an alternating emf is generated by loop of wire rotating in a magnetic field.
(b) A circular coil of radius 10 cm and 20 turns is rotated about its vertical diameter with angular speed of 50 rad s−1. in a uniform horizontal magnetic field of 3.0×10−2T.
(i) Calculate the maximum and average emf induced in the coil.
(ii) If the coil forms a closed loop of resistance 10Ω, calculate the maximum current in the coil and the average power loss due to Joule heating.
View SolutionA wire loop confined in a plane is rotated in its open plane with some angular velocity. A uniform magnetic field exists in the region. Find the emf induced in the loop.
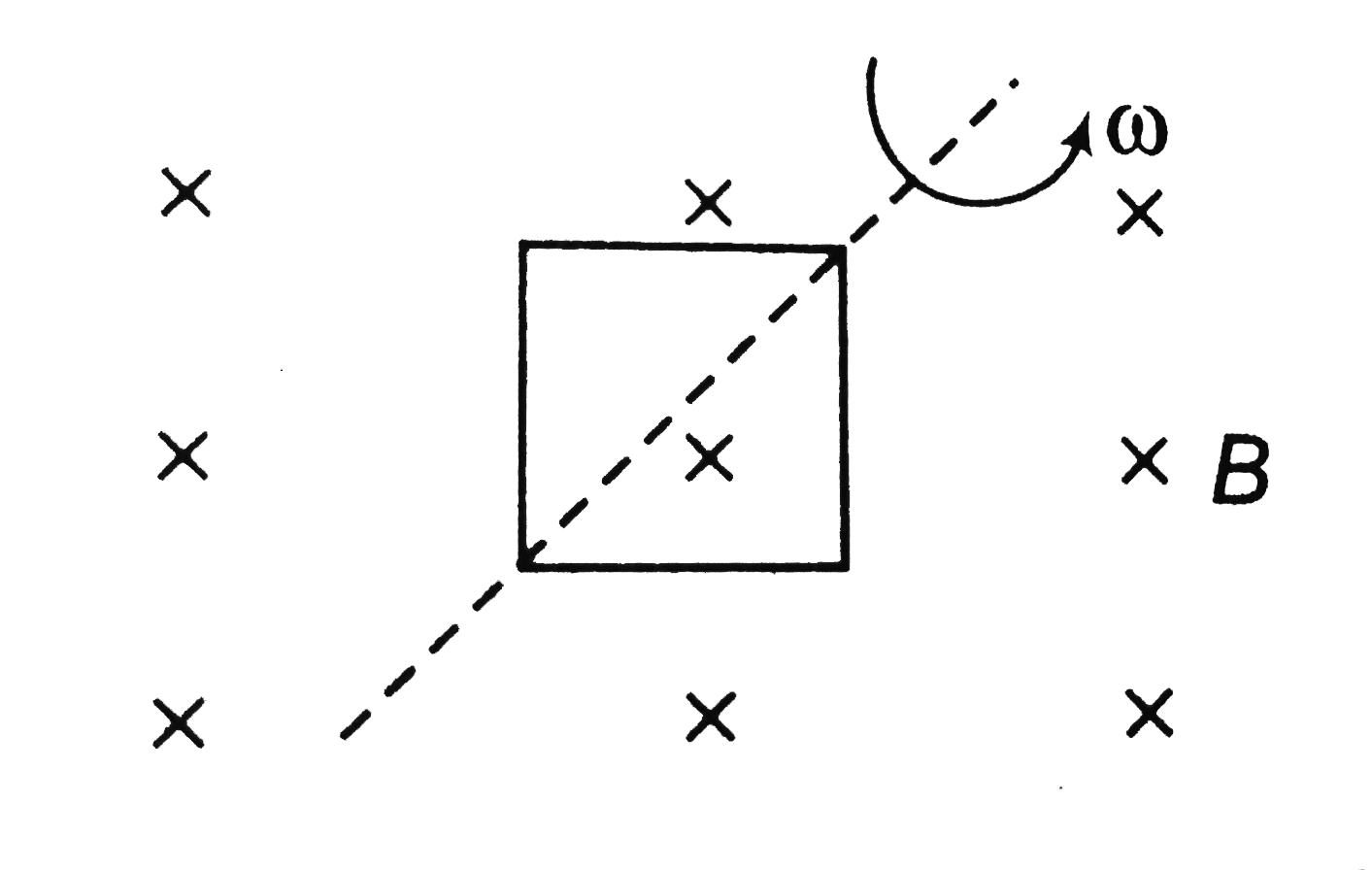
View SolutionA square loop of side b is rotated in a constant magnetic field B at angular frequency ω as shown in the figure. What is the emf induced in it?
View SolutionA horizontal straight wire of length L extending from east to west is falling with speed v at right angles to the horizontal component of Earth.s magnetic field B.
(i) Write the expression for the instantaneous value of the emf induced in the wire.
(ii) What is the direction of the emf?
(iii) Which end of the wire is at the higher potential?
View SolutionDraw a labelled diagram of Van de Graff generator. State its working principle to show how by introducing a small charged sphere into a larger sphere, a large amount of charge can be transferred to the outer sphere. State the use of this machine and also point out its limitations.
View SolutionState the working of a.c. generator with the help of a labelled diagram. The coil of an a.c. generator having N turns, each of area A, is rotated with a constant angular velocity ω. Deduce the expression for the alternating e.m.f. generated in the coil. What is the source of energy generation in this device?
View SolutionA semicircular loop of radius R is rotated with an angular velocity ω perpendicular to the plane of a magnetic field B as shown in the figure. Emf Induced in the loop is

View Solution
