A wire loop confined in a plane is rotated in its open plane with some angular velocity. A uniform magnetic field exists in the region. Find the emf induced in the loop.
To find the induced EMF in a wire loop that is rotated in a uniform magnetic field, we can follow these steps:
1. Identify the Given Information:
- A wire loop is rotating in its plane with an angular velocity ω.
- There is a uniform magnetic field B present in the region.
2. Understand the Concept of Magnetic Flux:
- The magnetic flux Φ through the loop is given by:
Φ=B⋅A=BAcosθ
- Here, A is the area vector of the loop, B is the magnetic field strength, and θ is the angle between the magnetic field and the area vector.
3. Determine the Angle θ:
- As the loop rotates, the angle θ changes with time. The angle at any time t can be expressed as:
θ=ωt
4. Express the Magnetic Flux as a Function of Time:
- Substitute θ into the magnetic flux equation:
Φ(t)=BAcos(ωt)
5. Apply Faraday's Law of Electromagnetic Induction:
- According to Faraday's law, the induced EMF E is given by the negative rate of change of magnetic flux:
E=−dΦdt
6. Differentiate the Magnetic Flux:
- Differentiate Φ(t) with respect to time:
dΦdt=ddt(BAcos(ωt))=BAddt(cos(ωt))
- The derivative of cos(ωt) is:
ddt(cos(ωt))=−ωsin(ωt)
- Therefore:
dΦdt=BA(−ωsin(ωt))=−BAωsin(ωt)
7. Calculate the Induced EMF:
- Substitute the expression for dΦdt back into the equation for induced EMF:
E=−(−BAωsin(ωt))=BAωsin(ωt)
Final Result:
The induced EMF in the rotating loop is given by:
E=BAωsin(ωt)
- A wire loop is rotating in its plane with an angular velocity ω.
- There is a uniform magnetic field B present in the region.
- The magnetic flux Φ through the loop is given by:
Φ=B⋅A=BAcosθ
- Here, A is the area vector of the loop, B is the magnetic field strength, and θ is the angle between the magnetic field and the area vector.
- As the loop rotates, the angle θ changes with time. The angle at any time t can be expressed as:
θ=ωt
- Substitute θ into the magnetic flux equation:
Φ(t)=BAcos(ωt)
- According to Faraday's law, the induced EMF E is given by the negative rate of change of magnetic flux:
E=−dΦdt
- Differentiate Φ(t) with respect to time:
dΦdt=ddt(BAcos(ωt))=BAddt(cos(ωt))
- The derivative of cos(ωt) is:
ddt(cos(ωt))=−ωsin(ωt)
- Therefore:
dΦdt=BA(−ωsin(ωt))=−BAωsin(ωt)
- Substitute the expression for dΦdt back into the equation for induced EMF:
E=−(−BAωsin(ωt))=BAωsin(ωt)
The induced EMF in the rotating loop is given by:
E=BAωsin(ωt)
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer9videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 210videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 27videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise8videos
ELECTROMAGNETIC WAVES
Similar Questions
A conducting loop confined in a plane is rotated in its own plane with some angular velocity.A uniform and constant magnetic field exist in the region.Find the current induced in the loop.
View SolutionA conducting rod OA of length l is rotated about its end O with an angular velocity ω in a uniform magnetic field directed perpendicualr to the rotation. Find the emf induced in the rod, between it's ends.
View SolutionA right angled triangle abc, made from a metallic wire, moves at a uniform speed v in its plane as shown in . A uniform magnetic field B exists in the perpendicular direction. Find the emf induced (a) in the loop abc, (b) in the segment bc, (c ) in the segment ac and (d) in the segment ab.
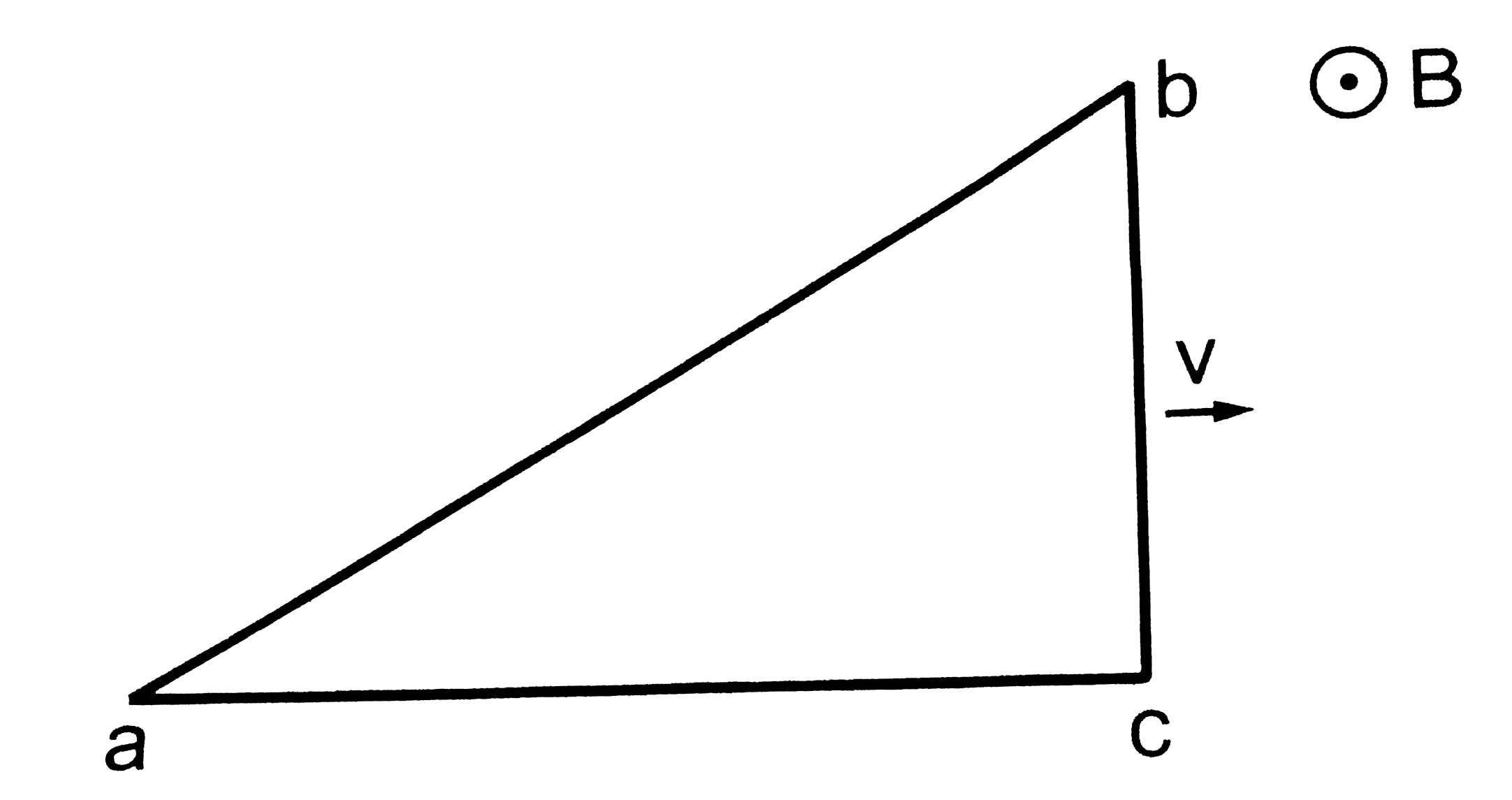 View Solution
View SolutionA copper wire bent in the shape of a semicircle of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the direction perpendicular to the plane of the wire. Find the emf induced between the ends of the wire if (a) the velocity is perpendicular ot the diameter joining free ends, (b) the velocity is parallel to this diameter.
View SolutionA square loop of edge a having n turns Is rotated with a uniform angular velocity ω about one of its diagonals which is kept fixed in a horizontal position . A uniform magnetic field B exists in the vertical direction. Find the emf induced in the coil.
 View Solution
View SolutionA square loop of side a is rotating about its diagonal with angular velocity ω in a perpendicular magnetic field →B It has 10 turns. The emf induced is
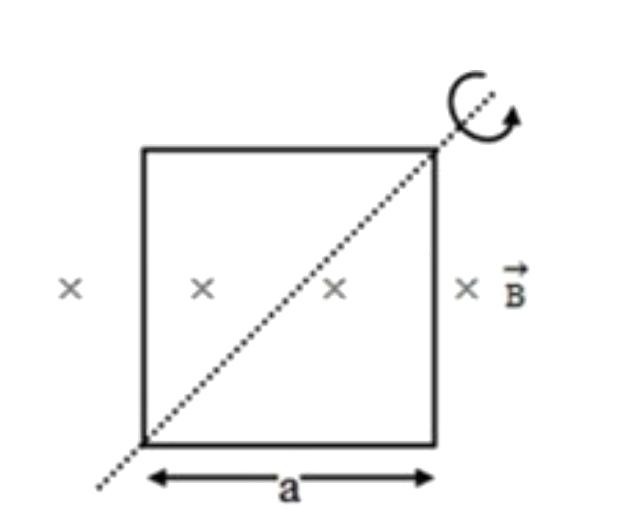 View Solution
View SolutionA right angled triangle abc made of a metallic wire, moves at a uniform speed v in its plane as shown in the figure.A uniform magnetic field B exists in the perpendicular direction of plane of triangle.Find the emf induced (a)in the loop abc. (b)in the segment bc,(c)in the segment ac and (d) in the segment ab.
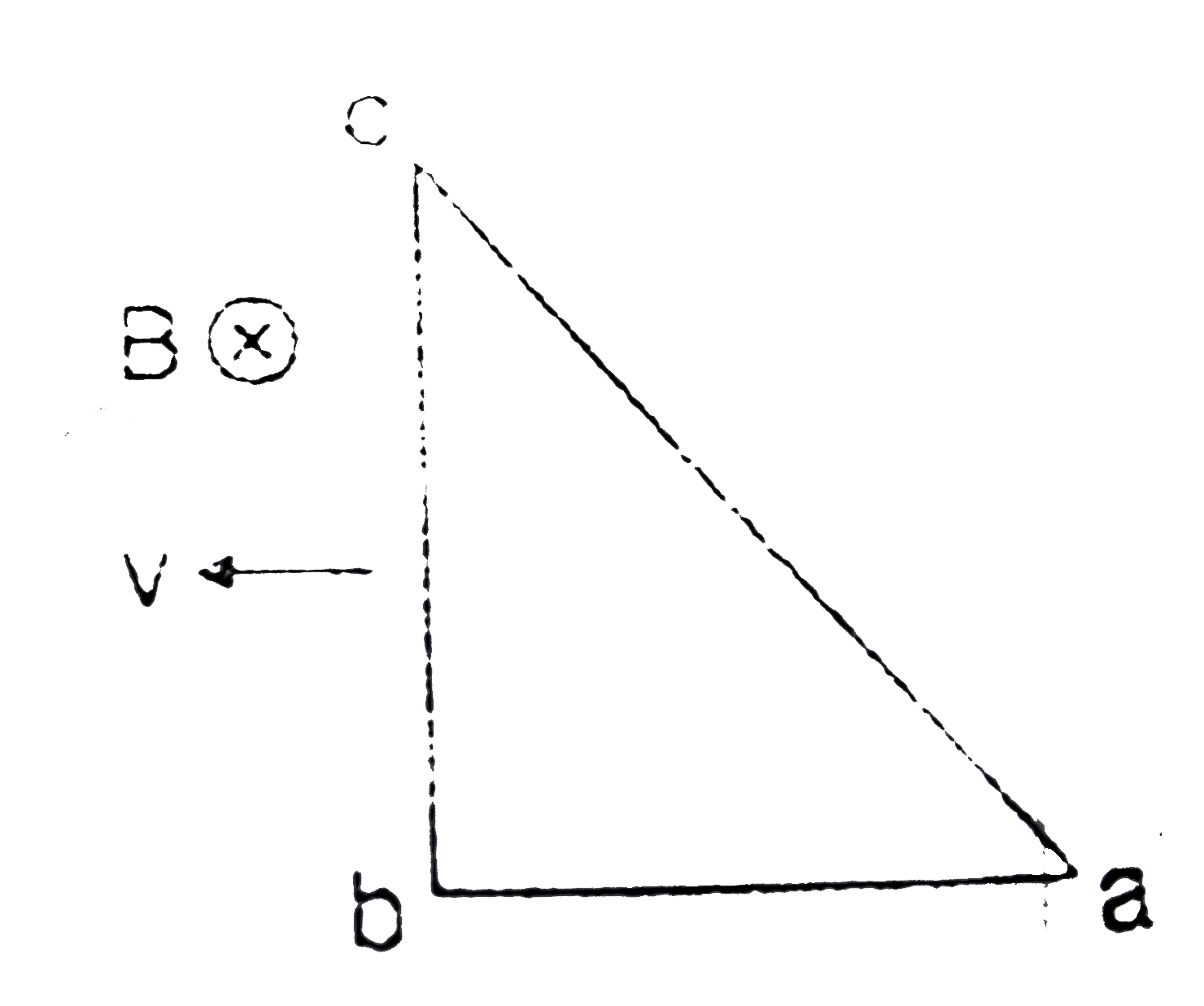 View Solution
View SolutionA circular loop of radius a having n turns is kept in a horizontal plane. A uniform magnetic field B exists in a vertical direction as shown in Fig.313. Find the emf induced in the loop if the loop is roated with a uniform angualr velocity ω about
(a) an axis passing through the center and perendicular to the plane of the loop.
(b) the diameter.
 View Solution
View SolutionA semicircular loop of radius R is rotated with an angular velocity ω perpendicular to the plane of a magnetic field B as shown in the figure. Emf Induced in the loop is
 View Solution
View SolutionA metallic loop is placed in a nonuniform magnetic field. Will an emf be induced in the loop?
View Solution

