A network of four capacitors each of 15μF capacitance is connected to a 500 V supply as shown in the figure . Determine (a) equivalent capacitance of the network and (b) charge on each capacitor .
To solve the problem, we will break it down into two parts: (a) finding the equivalent capacitance of the network and (b) determining the charge on each capacitor.
1. Identify the Configuration:
- Capacitors C1,C2, and C3 are in series.
- Capacitor C4 is in parallel with the equivalent capacitance of C1,C2, and C3.
2. Calculate the Equivalent Capacitance of Capacitors in Series:
- The formula for the equivalent capacitance Cs of capacitors in series is:
1Cs=1C1+1C2+1C3
- Since C1=C2=C3=15μF:
1Cs=115+115+115=315=15
- Therefore,
Cs=5μF
3. Calculate the Total Equivalent Capacitance of the Network:
- Now, add the equivalent capacitance Cs to C4 (which is also 15μF):
Ceq=Cs+C4=5μF+15μF=20μF
Part (b): Finding the Charge on Each Capacitor
1. Calculate Charge on Capacitor C4:
- The charge Q4 on capacitor C4 can be calculated using the formula:
Q=C⋅V
- For C4:
Q4=C4⋅V=15μF⋅500V=7500μC
2. Calculate Charge on Capacitors C1,C2, and C3:
- The charge Qs on the series combination (which is the same for C1,C2, and C3) can be calculated using:
Qs=Cs⋅V=5μF⋅500V=2500μC
Final Results
- (a) The equivalent capacitance of the network is 20μF.
- (b) The charge on each capacitor:
- Q1=Q2=Q3=2500μC
- Q4=7500μC
- Capacitors C1,C2, and C3 are in series.
- Capacitor C4 is in parallel with the equivalent capacitance of C1,C2, and C3.
- The formula for the equivalent capacitance Cs of capacitors in series is:
1Cs=1C1+1C2+1C3
- Since C1=C2=C3=15μF:
1Cs=115+115+115=315=15
- Therefore,
Cs=5μF
- Now, add the equivalent capacitance Cs to C4 (which is also 15μF):
Ceq=Cs+C4=5μF+15μF=20μF
- The charge Q4 on capacitor C4 can be calculated using the formula:
Q=C⋅V
- For C4:
Q4=C4⋅V=15μF⋅500V=7500μC
- The charge Qs on the series combination (which is the same for C1,C2, and C3) can be calculated using:
Qs=Cs⋅V=5μF⋅500V=2500μC
- (a) The equivalent capacitance of the network is 20μF.
- (b) The charge on each capacitor:
- Q1=Q2=Q3=2500μC
- Q4=7500μC
Topper's Solved these Questions
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET -III4videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - PHYSICS (Theory) [SET -I]25videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET -I29videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
A network of four each of 12μF capacitance is connected to a 500V apply as shown in Fig.
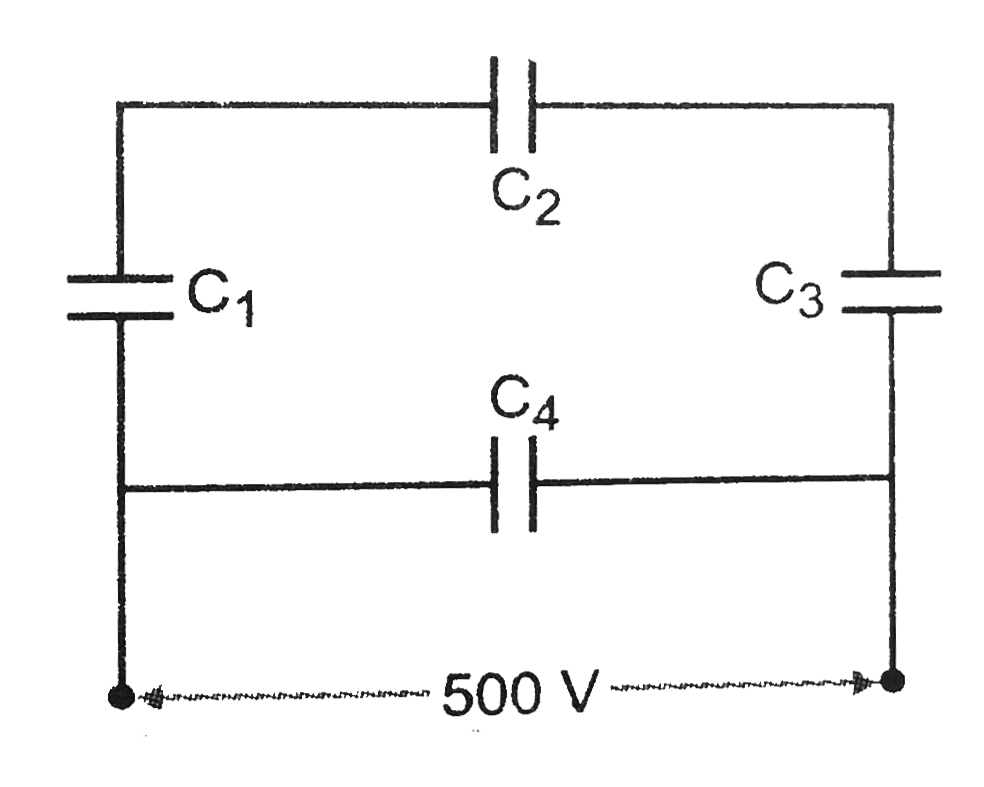
(a) Equivalent capacitance of the network.
(b) Charge on each capacitor.View SolutionA network of four 10μF capacitors is connected to a 500 V supply, as shown in Fig. Determine (a) the equivalent capacitance of the network and (b) the charge on each capacitor. (Note, the charge on a capacitor is the charge on the plate with higher potential, equal and opposite to the charge on the plate with lower potential.)
 View Solution
View SolutionA network of four 20 μF capacitors is connected to a 600 V supply as shoen in the figure.
The equivalent capacitance of the network is
 View Solution
View SolutionThe equivalent capacitance for the network shown in the figure is
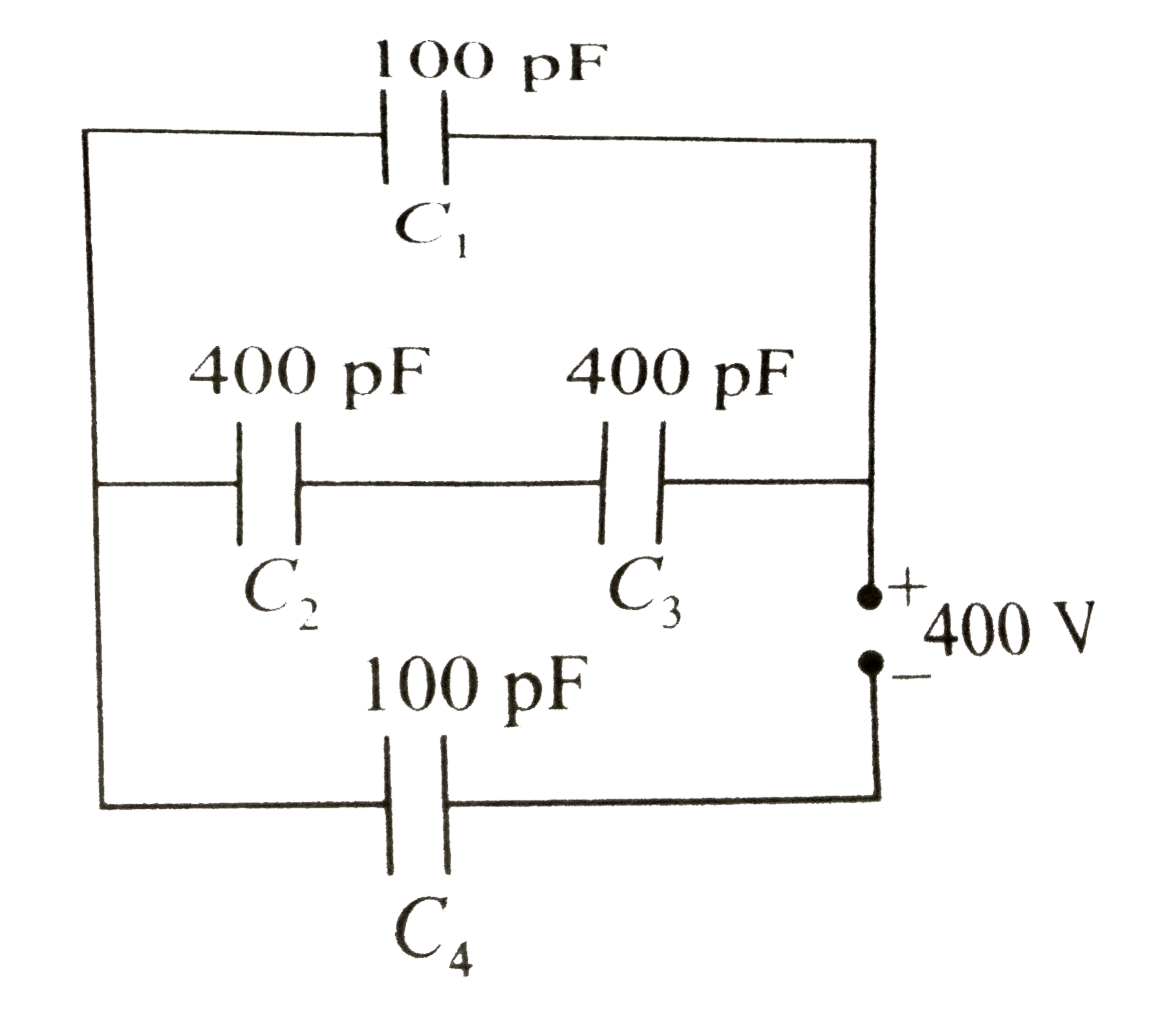 View Solution
View SolutionIn the circuit shown in figure find
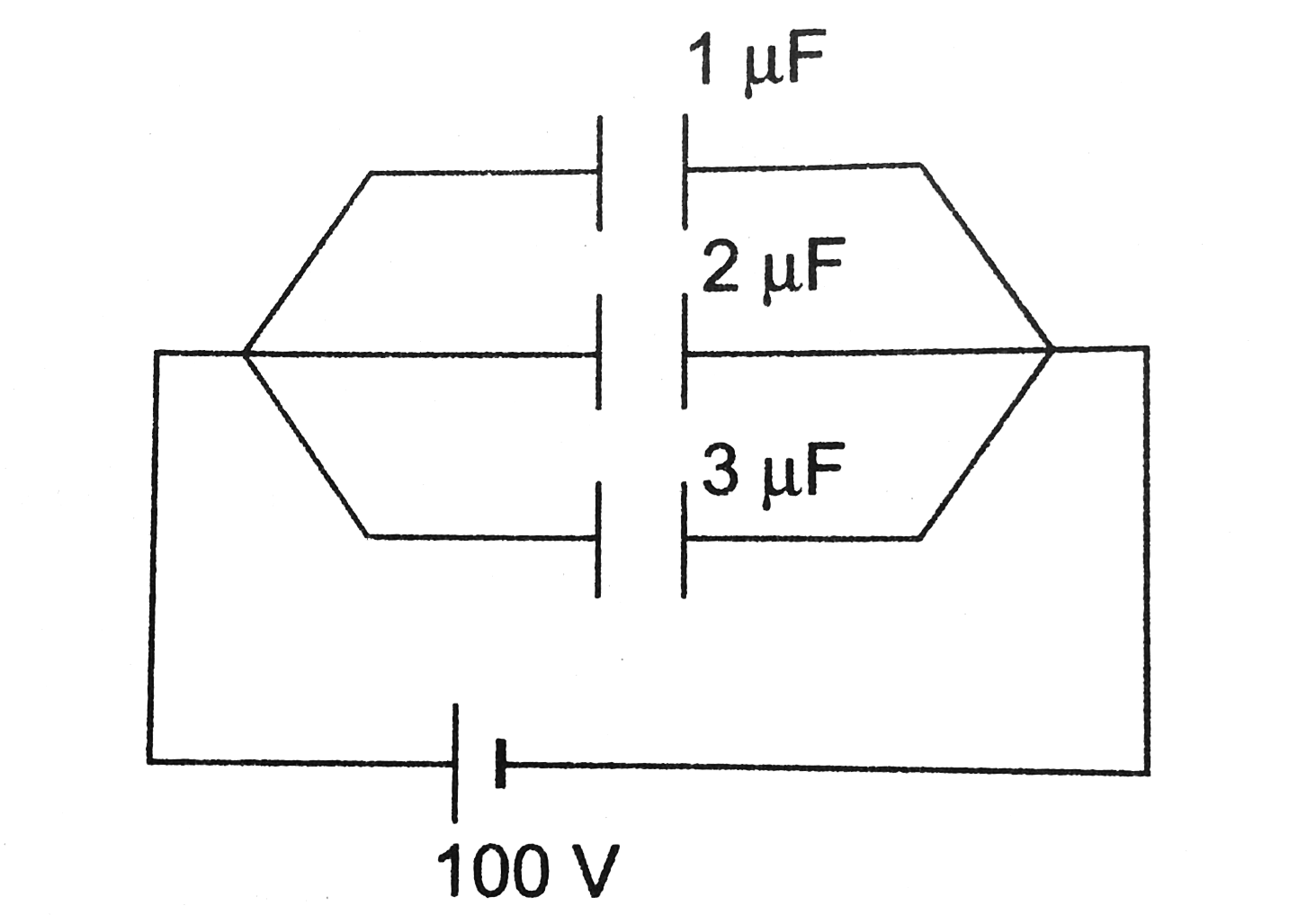
a. the equivalent capacitance and
b. the charge stored in each capacitor.View SolutionIn the circuit shown in figure find

a. the equivalent capacitance and
b. the charge stored in each capacitor.View SolutionIn the circuit shown in figure find

a. the equivalent capacitance and
b. the charge stored in each capacitor.View SolutionSix equal capacitors each of capacitance C are connected as shown in the figure. The equivalent capacitance between points A and B is
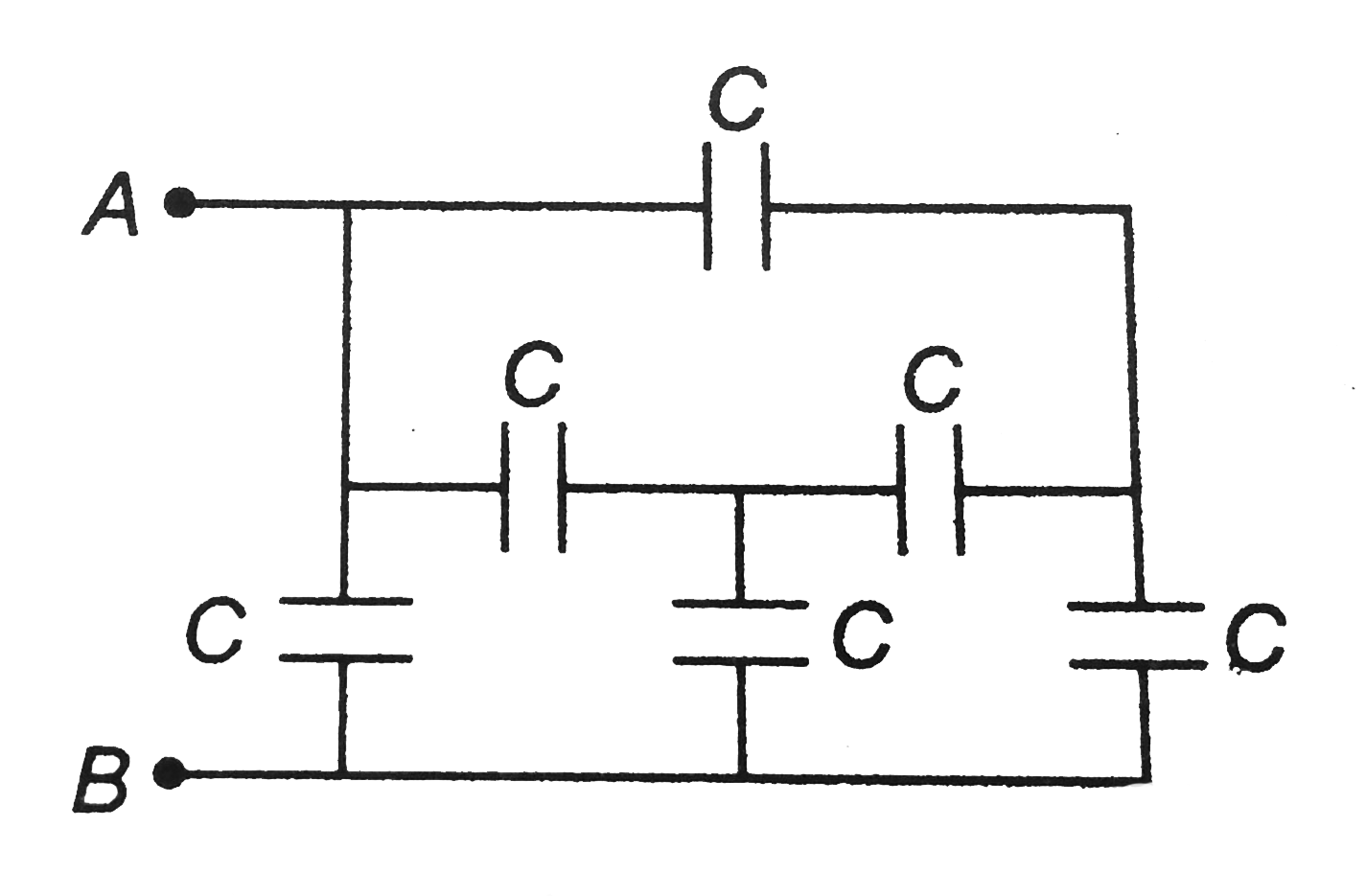 View Solution
View SolutionSix equal capacitors each of capacitance 10μF are connect as shown in the figure. Then the equivalent capacitance between A and B is
View SolutionAn infinite number of identical capacitors each of capacitance 1mF are connected as shown in the figure. Then the equivalent capacitance between A and B is.
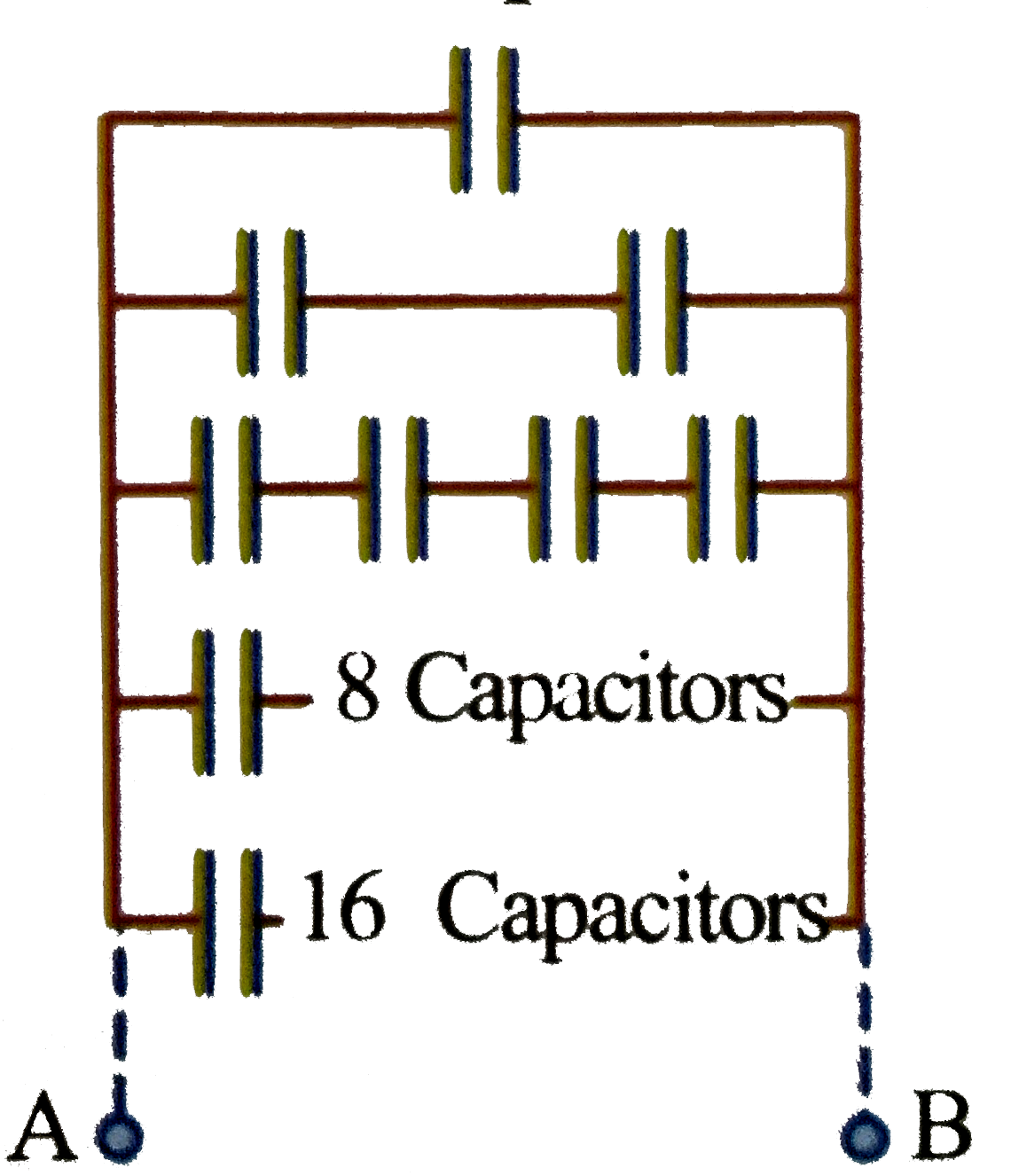 .View Solution
.View Solution


