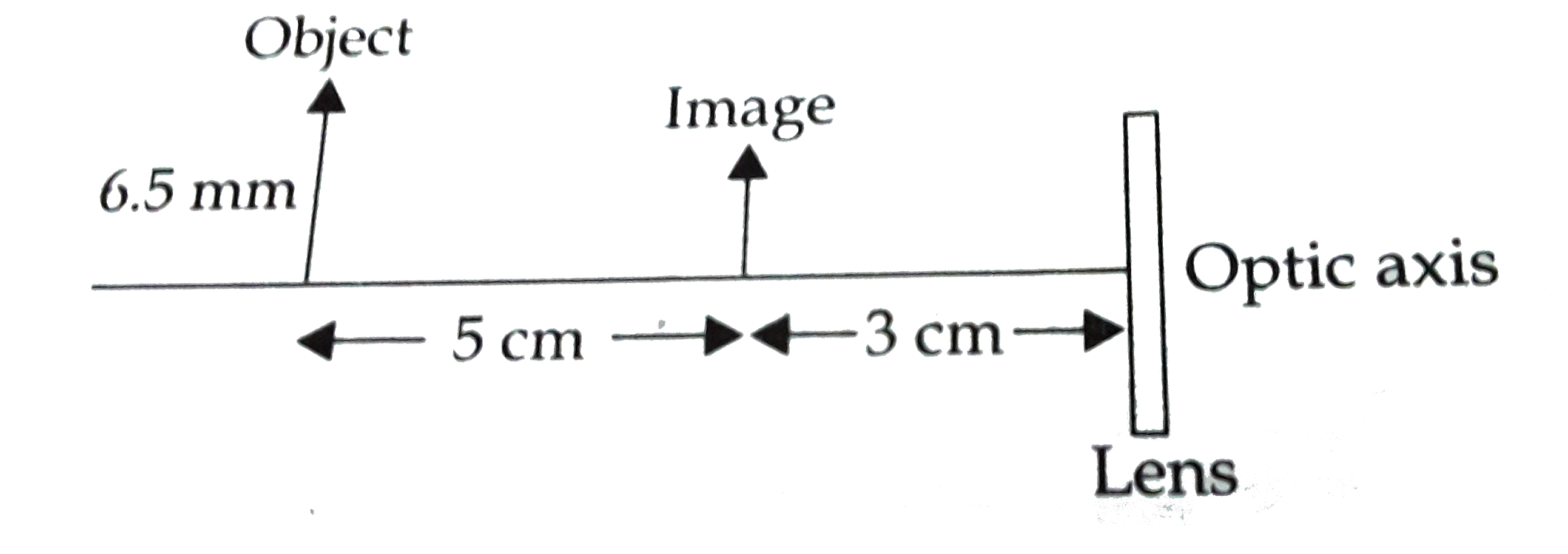
The image obtained with a convex lens is erect and its length is 4 times the length of the object. If the focal length of lens is 20cm, calculate the object and image distances.
To solve the problem, we will use the lens formula and the magnification formula for a convex lens.
1. Identify Given Values:
- Focal length of the lens, f=20cm (positive for a convex lens)
- Magnification, m=4 (the image is erect and 4 times the length of the object)
2. Understand Magnification:
- For a lens, magnification m is given by the formula:
m=vu
- Here, v is the image distance and u is the object distance. Since the image is erect and larger, we can write:
v=4u
3. Use the Lens Formula:
- The lens formula is given by:
1f=1v−1u
- Substituting f=20cm and v=4u into the lens formula:
120=14u−1u
4. Simplify the Equation:
- Rewrite the right side:
120=14u−44u=1−44u=−34u
- Therefore, we have:
120=−34u
5. Cross Multiply to Solve for u:
- Cross multiplying gives:
4u=−60⟹u=−15cm
- The negative sign indicates that the object is on the same side as the incoming light.
6. Calculate Image Distance v:
- Now substitute u back to find v:
v=4u=4×(−15)=−60cm
Final Answer:
- Object distance, u=−15cm
- Image distance, v=−60cm
- Focal length of the lens, f=20cm (positive for a convex lens)
- Magnification, m=4 (the image is erect and 4 times the length of the object)
- For a lens, magnification m is given by the formula:
m=vu
- Here, v is the image distance and u is the object distance. Since the image is erect and larger, we can write:
v=4u
- The lens formula is given by:
1f=1v−1u
- Substituting f=20cm and v=4u into the lens formula:
120=14u−1u
- Rewrite the right side:
120=14u−44u=1−44u=−34u
- Therefore, we have:
120=−34u
- Cross multiplying gives:
4u=−60⟹u=−15cm
- The negative sign indicates that the object is on the same side as the incoming light.
- Now substitute u back to find v:
v=4u=4×(−15)=−60cm
- Object distance, u=−15cm
- Image distance, v=−60cm
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET -III
4 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - PHYSICS (Theory) [SET -I]
25 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET -I
29 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
Knowledge Check
The size of the image of an object, which is at infinity, as formed by a convex lens of focal length 30 cm is 2 cm. If a concave lens of focal length 20 cm is placed between the convax lens and the image at a distance of 26 cm from the convex lens, calculate the new size of the image.
A1.25cmB2.5cmC1.05cmD2cm
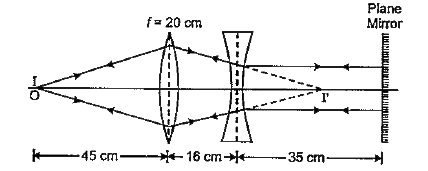
The figure below shows the positions of a point object 0, two lenses, a plane mirror and the final image I which coincides with the object. The focal length of the convex lens is 20 cm. Calculate the focal length of the concave lens.
View SolutionA lens of focal length 12cm forms an upright image three times the size of a real object. Find the distance in cm between the object and image.
View SolutionA convex lens of focal length f forms an image which is 1/3 times the size of the object. Then, the distance of object from the lens is
View SolutionA convex lens of focal length f produces an image 1n times than that of the size of the object. The distance of the object from the lens is:
View SolutionFocal length of the convex lens shown in figure is 20cm. Find the image position and image velocity.
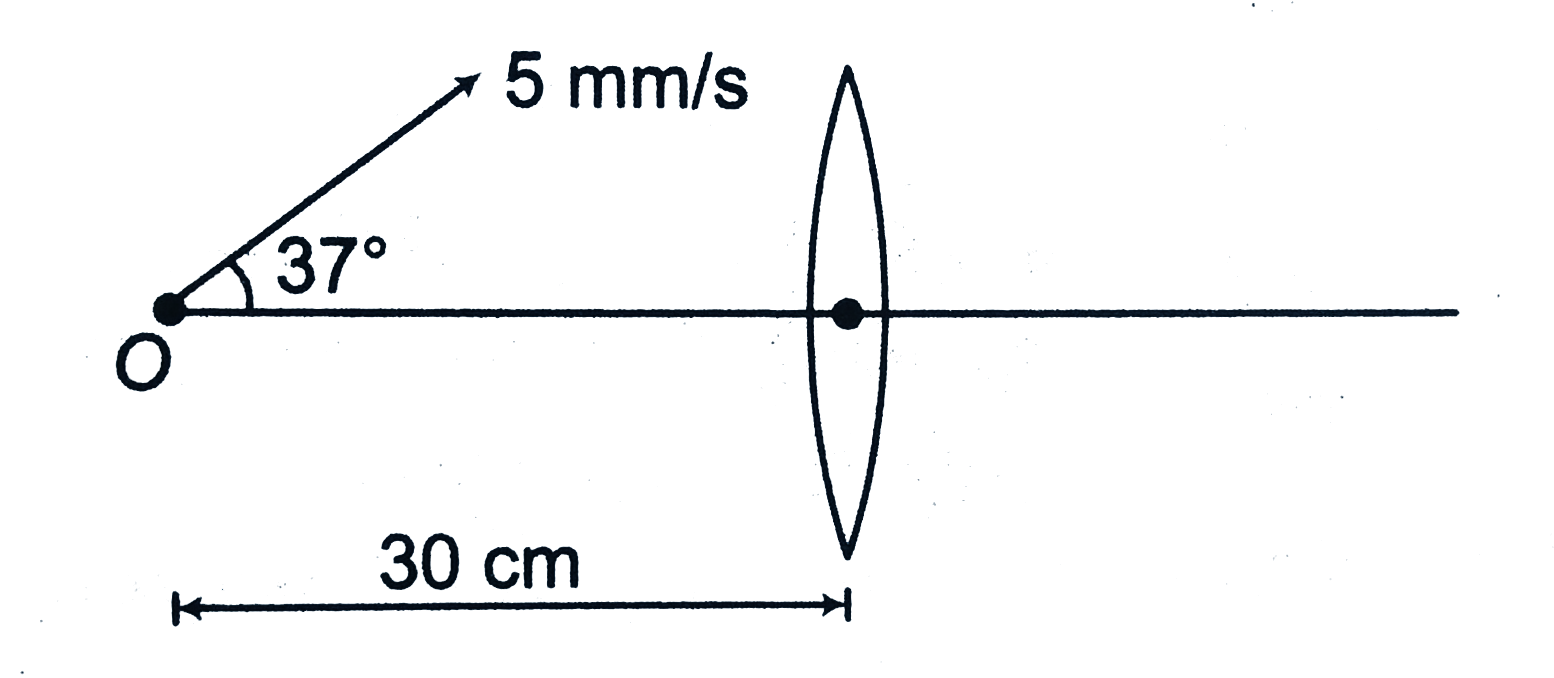
View SolutionFind the distance of an object from a convex lens if image is
two times magnified. Focal length of the lens is 10cm
View SolutionFind the distance of an object from a convex lens if image is
two times magnified. Focal length of the lens is 10cm
View Solution