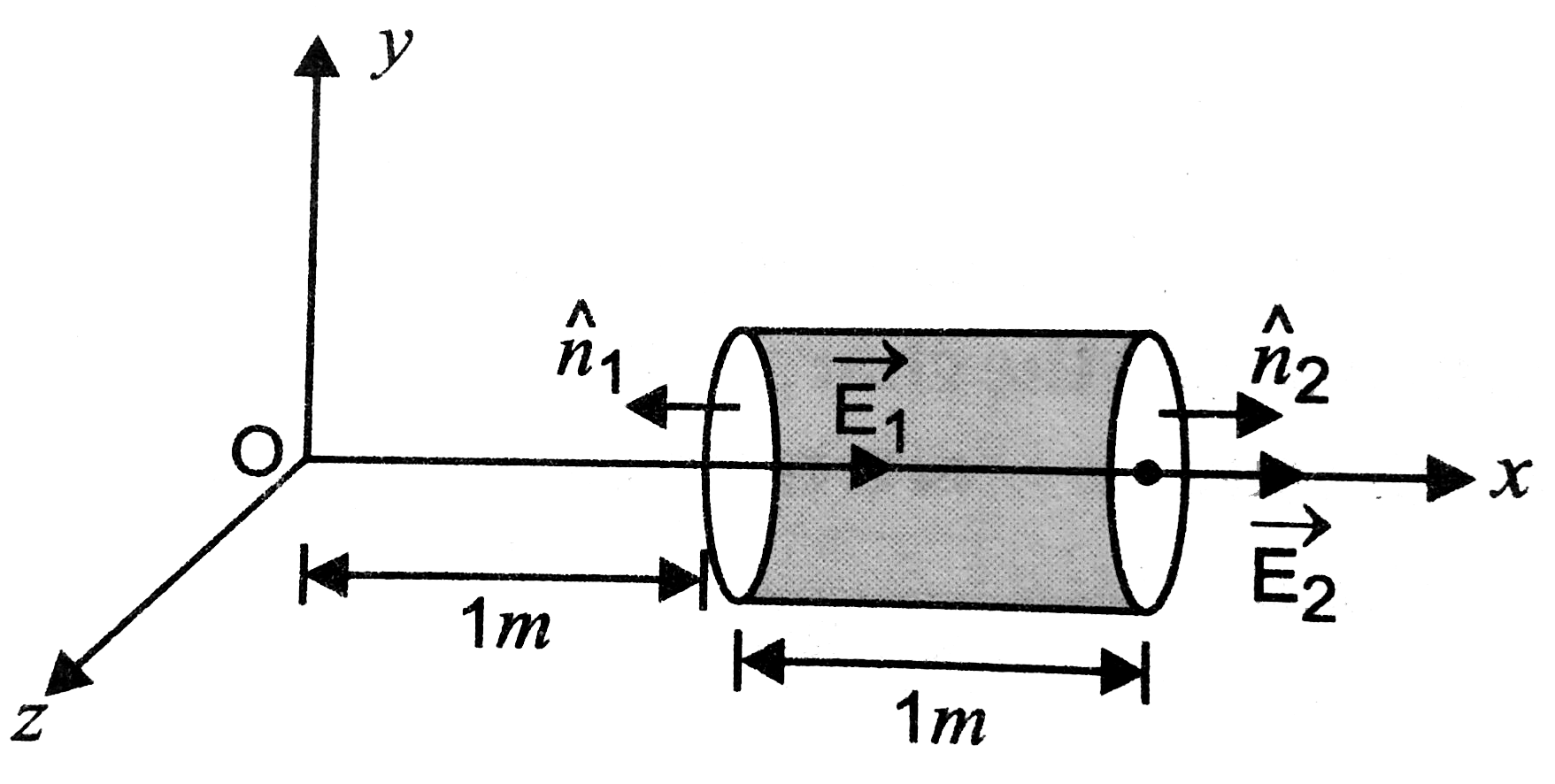
A bollow cylindrical box of length 1m and area of cross section $25 c m^{2}$ is placed in a three dimensional co-ordinate system as shown in Fig, The electric field in the
region is given by $\to E = 50 x ˆ i$ , where E is in $N C^{- 1}$ and x is in meter. Find
(i) Net flux through the cylinder
(ii) Charge enclosed by the cylinder.

Video Solution

Answer

Step by step video & image solution for A bollow cylindrical box of length 1m and area of cross section 25 cm^(2) is placed in a three dimensional co-ordinate system as shown in Fig, The electric field in the region is given by vec(E) = 50 x hat(i) , where E is in NC^(-1) and x is in meter. Find (i) Net flux through the cylinder (ii) Charge enclosed by the cylinder. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

A hollow cylindrical box of length 0.5m and area of cross-section $20 c m^{2}$ is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by $\to E = 20 x ˆ i$ , where E is $N C^{- 1}$ and x is in meters, Find

(i) Net flux through the cylinder.
(ii) Charge enclosed in the cylinder.
View Solution
The electric field in a region is given by $E = a ˆ i + b ˆ j$ . Hence as and b are constants. Find the net flux passing through a square area of side $I$ parallel to y-z plane.
View Solution
The electric field in a region is given by $E = a ˆ i + b ˆ j$ . Hence as and b are constants. Find the net flux passing through a square area of side $I$ parallel to y-z plane.
View Solution
Electric field in a region is given by $\to E = - 4 x ˆ i + 6 y ˆ j$ . Then find the charge enclosed in the cube of side 1m oriented as shown in the diagram

View Solution
The electric field in a region is given by $E = \frac{3}{5} E_{0} ˆ i + \frac{4}{5} E_{0} j$ with $E_{0} = 2.0 \times 10^{3} N / C$ . Find the flux of this field through a rectangular surface of area $0.2 m^{2}$ parallel to the y-z plane.
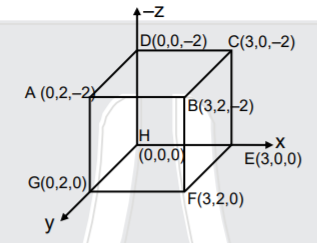
View Solution
A cube has sides of length $L = 0.300 m$ . It is placed with one corner at the origin ( refer to Fig.2.119).The electric field is not uniform but is given by $\to E = (- 5.00 N C^{- 1}) x ˆ i + (3.00 N C^{- 1}) z ˆ k$ .
The flux passing through the surface $S_{5}$ will be
View Solution
If electric field in the space is given by, $\to E = 4 x ˆ i + (y^{2} + 1) ˆ j$ and electric flux through ABCD is $ϕ_{1}$ and electric flux through BCEF is $ϕ_{2}$ , then find ( $ϕ_{1} - ϕ_{2}$ )
View Solution
The electric field in a region is given by $\to E = \frac{3}{5} E_{0} \to i + \frac{4}{5} E_{0} \to j$ with $E_{0} = 2.0 \times 10^{3} N C^{- 1}$ . Find the flux of this field through a recatngular surface of area $0.2 m^{2}$ parallel to the y-z plane.
View Solution
State Gauss’s law in electrostatics. A cube with each side a is kept in an electric field given by E = Cx (as shown in the figure) where C is a positive dimensional constant. Find out :

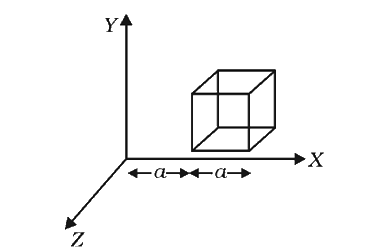
(i) The electric flux through the cube (ii) The net charge inside the cube.
View Solution
A cube has sides of length $L$ . It is placed with one corner at the origin ( refer to Fig.2.119). The electric field is uniform and given by $\to € = - B ˆ i + C ˆ j - D ˆ k$ , where $B, C, and D$ are positive constants.
The total flux passing through the cube is
View Solution

Similar Questions

Recommended Questions