The electric field in a region is given by E=aˆi+bˆj. Hence as and b are constants. Find the net flux passing through a square area of side I parallel to y-z plane.
To find the net electric flux passing through a square area of side I that is parallel to the y-z plane, we can follow these steps:
Step 1: Understand the Electric Field and Area Vector
The electric field is given by:
E=A^i+B^j
where A and B are constants. The square area is parallel to the y-z plane, which means it is oriented along the x-axis.
Step 2: Define the Area Vector
For a square of side I in the y-z plane, the area vector A is directed along the x-axis. The magnitude of the area is:
A=I2
Thus, the area vector can be expressed as:
A=I2^i
Step 3: Calculate the Electric Flux
The electric flux Φ through a surface is given by the dot product of the electric field and the area vector:
Φ=E⋅A
Substituting the expressions for E and A:
Φ=(A^i+B^j)⋅(I2^i)
Step 4: Perform the Dot Product
Using the properties of the dot product:
Φ=A^i⋅(I2^i)+B^j⋅(I2^i)
Since ^j⋅^i=0 (the two unit vectors are perpendicular), the second term vanishes:
Φ=AI2
Step 5: Final Result
Thus, the net electric flux passing through the square area is:
Φ=AI2
The electric field is given by:
E=A^i+B^j
where A and B are constants. The square area is parallel to the y-z plane, which means it is oriented along the x-axis.
For a square of side I in the y-z plane, the area vector A is directed along the x-axis. The magnitude of the area is:
A=I2
Thus, the area vector can be expressed as:
A=I2^i
The electric flux Φ through a surface is given by the dot product of the electric field and the area vector:
Φ=E⋅A
Substituting the expressions for E and A:
Φ=(A^i+B^j)⋅(I2^i)
Using the properties of the dot product:
Φ=A^i⋅(I2^i)+B^j⋅(I2^i)
Since ^j⋅^i=0 (the two unit vectors are perpendicular), the second term vanishes:
Φ=AI2
Thus, the net electric flux passing through the square area is:
Φ=AI2
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 5
5 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 6
4 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
The electric field in a region is given by E=αxˆi. Here α is a constant of proper dimensions. Find
a. the total flux passing throug a cube bounded by the surface x=l,x=2l,y=0,y=l,z=0,z=l.
b. the charge contained inside in above cube.
View SolutionThe electric field in a region is given by →E=E0axˆi. Find the electric flux passing through a cubical volume bounded by the surfaces x=0,x=a,y=0,y=a,z=0 and z=a.
View SolutionA cube has sides of length L. It is placed with one corner at the origin as shown in figure. The electric field is uniform and given by E=−Bˆi+Cˆj−Dˆk, where B, C and D are positive constants.
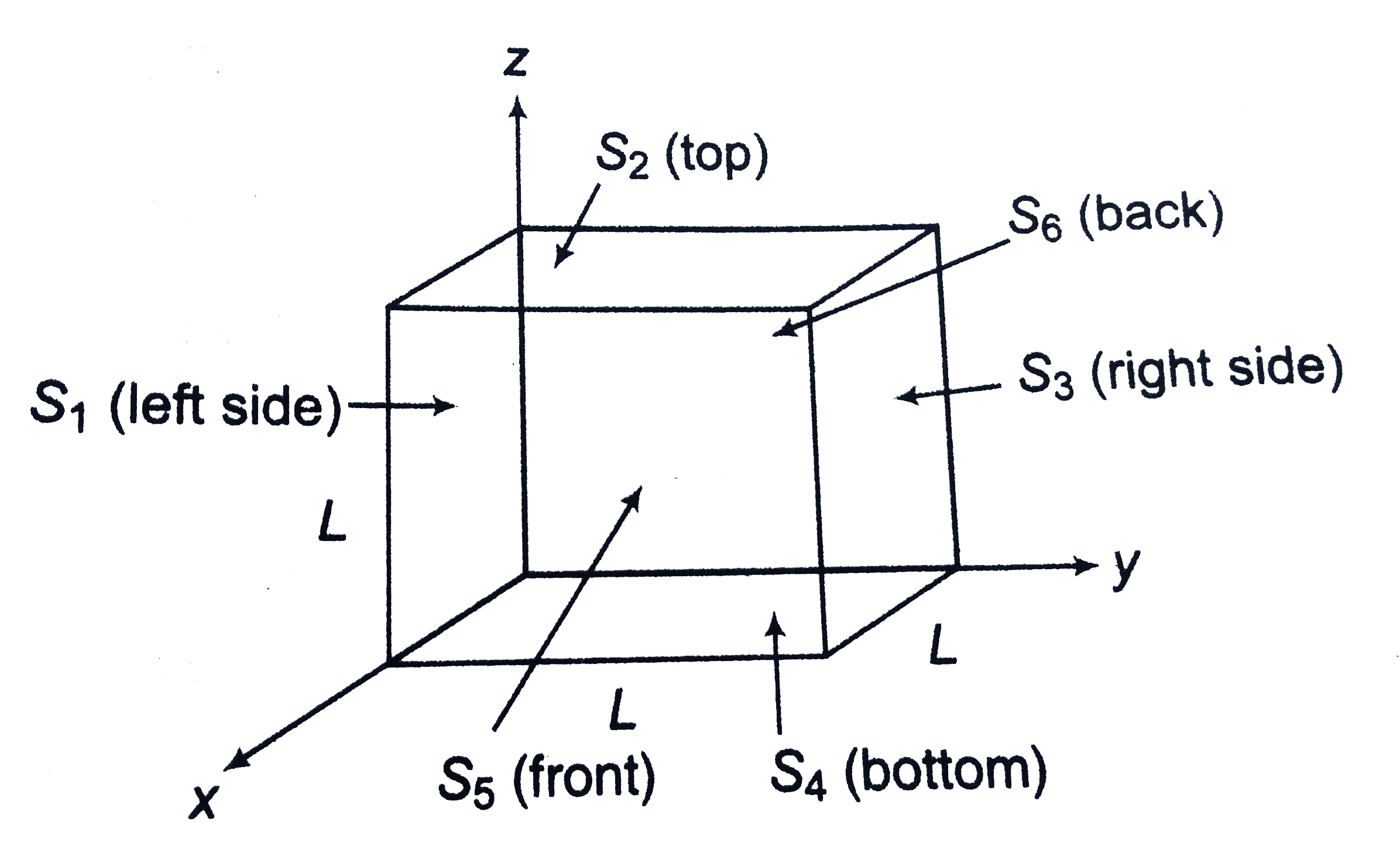
(a) Find the electric flux through each of the six cube faces S1,S2,S3,S4andS5andS6.
(b) Find the electric flux through the entire cube.
View SolutionThe electric field in a region of space is given by E=5ˆi+2ˆjN/C. The flux of E due ot this field through an area 1m2lying in the y-z plane, in SI units is
View SolutionThe electric field in a region is given by E=35E0ˆi+45E0j with E0=2.0×103N/C. Find the flux of this field through a rectangular surface of area 0.2m2 parallel to the y-z plane.
View SolutionIf the electric field is given by 3ˆi+2ˆj+6ˆk . Find the electric flux through a surface area 20 unit lying in xy plane
View SolutionWrite the equation of the plane passing through (2, -1,1) and parallel to the plane 3x+2y−z=7.
View SolutionA cube has sides of length L. It is placed with one corner at the origin ( refer to Fig.2.119). The electric field is uniform and given by →€=−Bˆi+Cˆj−Dˆk , where B,C,andD are positive constants.
The total flux passing through the cube is
View SolutionThe electric field in a region is given by →E=35E0→i+45E0→j with E0=2.0×103NC−1. Find the flux of this field through a recatngular surface of area 0.2m2 parallel to the y-z plane.
View SolutionA square of side L meters lies in the x-y plane in a region, where the magnetic field is given by B=B0(2ˆi+3ˆj+4ˆk)T, where B0 is constant. The magnitude of flux passing through the square is
View Solution
