A wire AB is carrying a steady current of 10A and is lying on the table. Another wire CD carrying 6A is held directly above AB at a height of 2 mm. Find the mass per unit length of the wire CD so that it remains suspended at its position when left free. Give the direction of the current flowing in CD with respect to that in AB. [Take the value of g=10ms−2]
To solve the problem, we need to find the mass per unit length of wire CD so that it remains suspended when left free. We will use the principles of electromagnetism and the balance of forces acting on the wire.
1. Identify the Forces Acting on Wire CD:
- The downward force acting on wire CD is its weight, which can be expressed as:
Fweight=m⋅g
- The upward force acting on wire CD is the magnetic force due to the current in wire AB.
2. Magnetic Force Between Two Parallel Wires:
- The magnetic force per unit length between two parallel wires carrying currents I1 and I2 is given by:
FB=μ0I1I22πd
- Here, d is the distance between the two wires, which is given as 2 mm (or 2×10−3 m).
3. Setting Up the Equation:
- For wire CD to remain suspended, the magnetic force must balance the weight:
FB=Fweight
- Therefore, we have:
μ0I1I22πd=m⋅g
4. Expressing Mass per Unit Length:
- The mass per unit length mL can be expressed as:
mL=FBg
- Substituting for FB:
mL=μ0I1I22πdg
5. Substituting Known Values:
- Given:
- I1=10A
- I2=6A
- d=2×10−3m
- g=10m/s2
- μ0=4π×10−7T m/A
- Plugging in these values:
mL=(4π×10−7)⋅(10)⋅(6)2π⋅(2×10−3)⋅(10)
6. Simplifying the Expression:
- Cancel out π:
mL=(4×10−7)⋅(10)⋅(6)2⋅(2×10−3)⋅(10)
- This simplifies to:
mL=(4×6)2⋅2×10−4=244×10−4=6×10−4kg/m
7. Final Answer:
- The mass per unit length of wire CD is:
mL=6×10−4kg/m
8. Direction of Current in Wire CD:
- Since the magnetic force is repulsive, the current in wire CD must flow in the opposite direction to that in wire AB.
- The downward force acting on wire CD is its weight, which can be expressed as:
Fweight=m⋅g
- The upward force acting on wire CD is the magnetic force due to the current in wire AB.
- The magnetic force per unit length between two parallel wires carrying currents I1 and I2 is given by:
FB=μ0I1I22πd
- Here, d is the distance between the two wires, which is given as 2 mm (or 2×10−3 m).
- For wire CD to remain suspended, the magnetic force must balance the weight:
FB=Fweight
- Therefore, we have:
μ0I1I22πd=m⋅g
- The mass per unit length mL can be expressed as:
mL=FBg
- Substituting for FB:
mL=μ0I1I22πdg
- Given:
- I1=10A
- I2=6A
- d=2×10−3m
- g=10m/s2
- μ0=4π×10−7T m/A
- Plugging in these values:
mL=(4π×10−7)⋅(10)⋅(6)2π⋅(2×10−3)⋅(10)
- Cancel out π:
mL=(4×10−7)⋅(10)⋅(6)2⋅(2×10−3)⋅(10)
- This simplifies to:
mL=(4×6)2⋅2×10−4=244×10−4=6×10−4kg/m
- The mass per unit length of wire CD is:
mL=6×10−4kg/m
- Since the magnetic force is repulsive, the current in wire CD must flow in the opposite direction to that in wire AB.
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [SET - I]
28 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [SET - II DELHI BOARD]
5 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET - III (Delhi Board)
6 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
A wire AB is carrying a steady current of 12 A and is lying on the table. Another wire CD carrying 5 A is held directly above AB at a height of 1mm. Find the mass per unit length of the wire CD so that it remains suspended at its position when left free. Give the direction of the current flowing in CD with respect to that in AB. [Take the value of g=10ms−2]
View SolutionThe resistance per unit length of the wires in segments AB, BC, CD, and AD are the same. The magnetic field due to the current at point O is
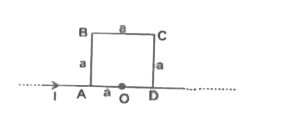
View Solution
Knowledge Check
In the figure, if AB = 10, what is the length of the side CD ?
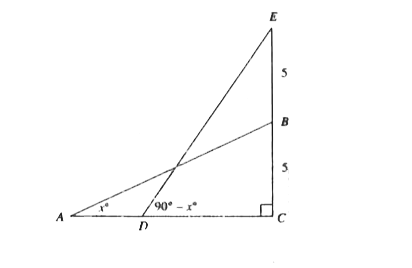 A5B5√3C10√3D10
A5B5√3C10√3D10
A long horizontal wire P carries a current of 50A. It is rigidly fixed. Another wire Q is placed directly above and parallel to P, as shown in figure below. The weight per unit length of the wire Q is 0.025 Nm−1 and it carries a current of 25A. Find the distance .r. of the wire Q from the wire P so that the wire Q remains at rest.
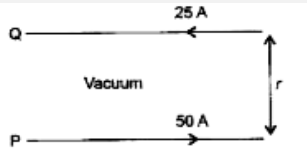
View SolutionA wire is bent in the form of a circular arc with a straight portion AB. Magnetic induction at O when current flowing in the wire, is

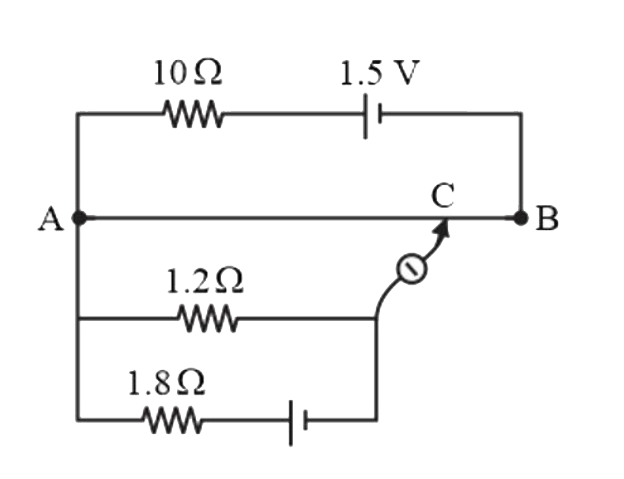
View SolutionIn the below circuit , AB is a wire of length 100 cm with 5Ω resistance . If there is no deflection in the galvanometer , the current flowing in the wire AB is
View SolutionTwo long parallel copper wires carry current of 5A each in opposite directions. If the wires are separated by a distance distance of 0.5m, then the force per unit length between the two wires is
View SolutionA current I1 carrying wire AB is placed near another long wire CD carrying current I2. If wire AB is free to move, it will have
View SolutionTwo parallel wires carry currents of 20A and 40A in opposite directions. Another wire carrying a current antiparallel to 20A is placed midway between the two wires. The magnetic force on it will be
View SolutionA straight wire of diametre 0.5 mm carrying a current of 1 A is replaced by another wire of 1mm diametre carrying same current. The strenth of magnetic field far away is
View Solution
